This is a continuation of a series of posts on the Nikon D850. The series starts here. You should be able to find all the posts about that camera in the Category List on the right sidebar, below the Articles widget. There’s a drop-down menu there that you can use to get to all the posts in this series; just look for “D850”.
In this post, I looked at FocusTune analyses of the Nikon 70-200/2.8E lens. Several folks criticised my using FocusTune to look at phase-detect autofocus (PDAF) variability in the D850, correctly pointing out that it is a black box and we don’t know exactly what it’s measuring.
For the last couple of days, I’ve been writing code to do something similar, but in a way that I understand.
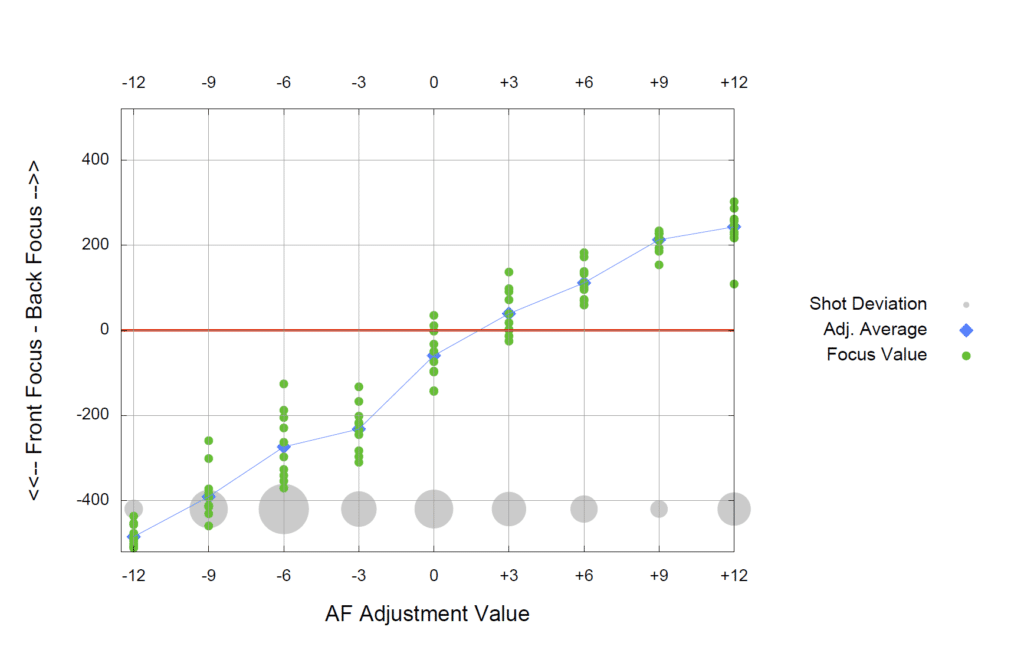
Let’s go back to one of the graphs from the earlier post, with the lens set to f/2.8 and 200 mm.
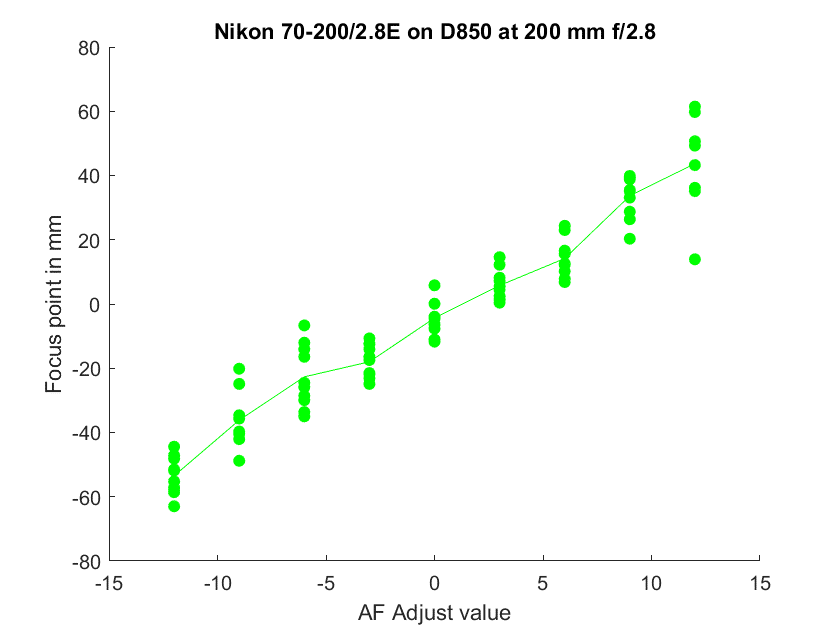
Here is a plot from my code with the same image set:
I’ve just plotted the green channel of the AdobeRGB JPEG images. Presumably, FocusTune uses a luminance measure. That turns out not to be important here, as we’ll see further on. Both plots say that the right AF adjustment value is +3. The FocusTune plot is prettier — give me time; I’ve just started this project. One difference is that my vertical axis is calibrated; it’s the shift of the focus point in millimeters, with positive numbers indicating shifts away from the camera (back-focusing) and negative ones indicating shifts towards the camera (front-focusing).
The sharpness measure I am using is Brenner’s focus criterion (Santos, A.; de Solorzano, C. O.; Vaquero, J. J.; Peña, J. M.; Mapica, N. & Pozo, F. D. “Evaluation of autofocus functions in molecular cytogenetic analysis”. 1997. I’m using some code that lets me pick from a wide variety of such criteria. Brenner’s was only the second one I tried, as seems to work quite well if the data is properly smoothed. The smoothing that I’m using is one of the options in Matlab’s smoothdata function. Here’s what Matlab has to say about the smoothing option I’m using:
'rloess'— Robust quadratic regression over each window ofA. This method is a more computationally expensive version of the method'loess', but it is more robust to outliers.
I tried fitting a double Gaussian with Nelder-Mead, and that works most of the time and is probably fractionally better, but it fails to converge properly about 3% of the time, and it computationally expensive, so I dropped it.
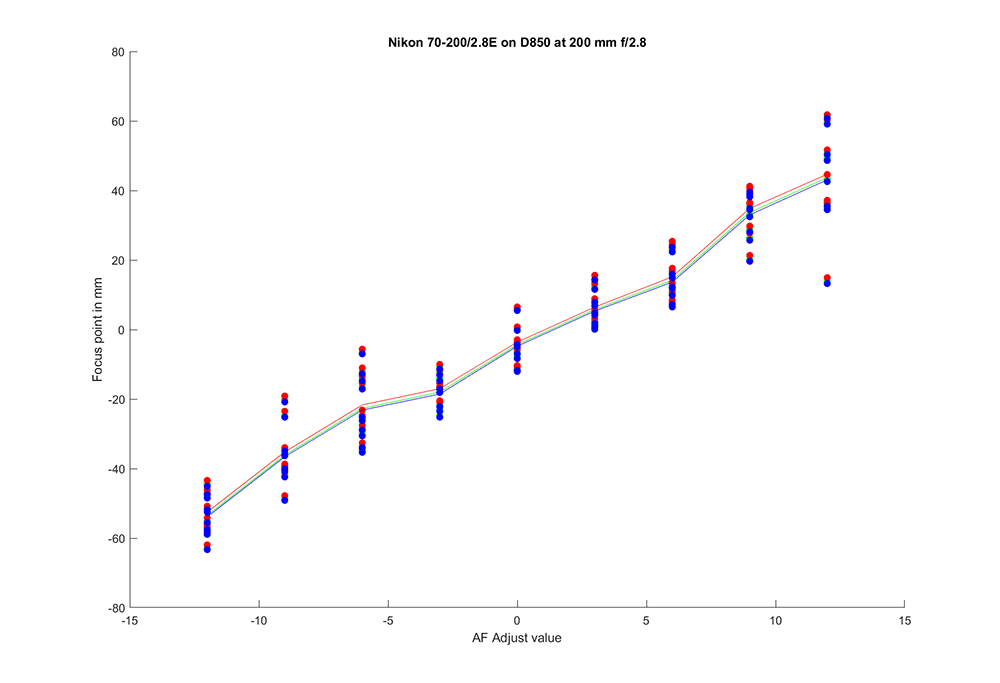
Here’s what all three channels look like:
As you can see, the variation in the channels due to longitudinal chromatic aberration (LoCA) is small compared to that of the PDAF system. The red channel tends to focus behind the green and blue ones.
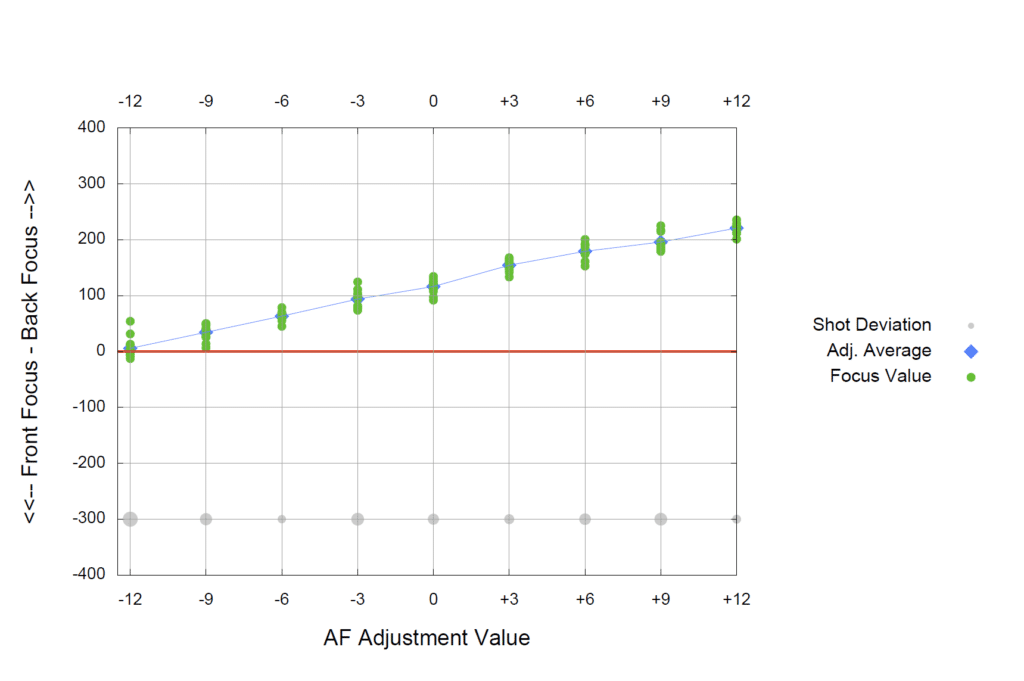
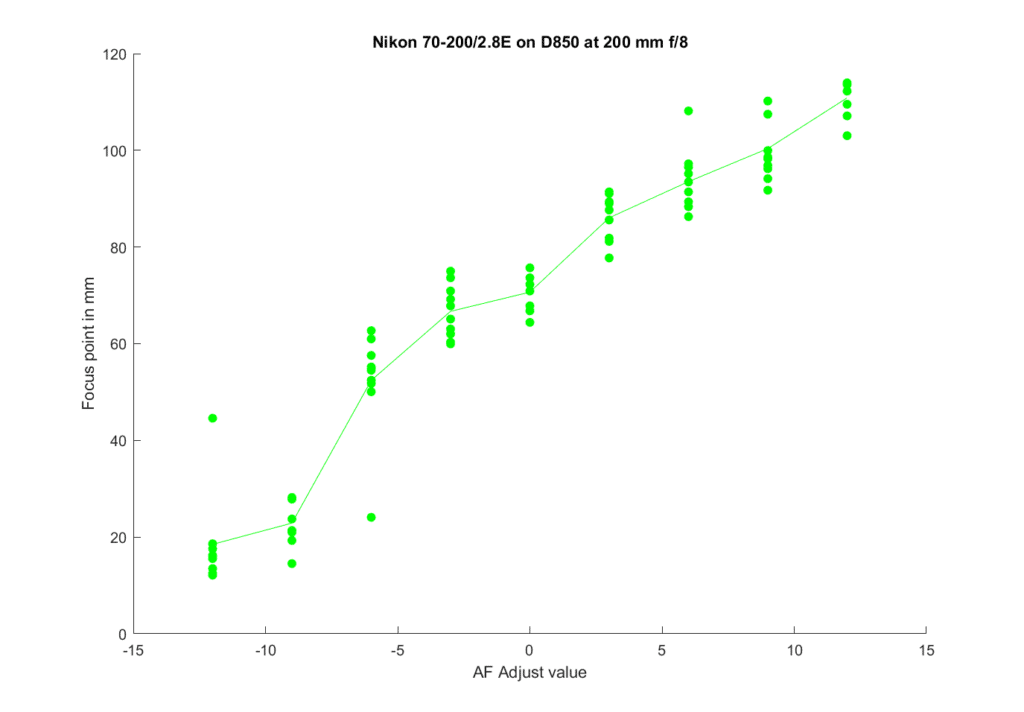
Here’s what FocusTune thought about the same lens at the same focal length, but at f/8:
Note that the variation along the vertical axis is about a third of what it was at f/2.8. I found that curious. The scatter is also less. That is strange as well, if the vertical axis is a distance measure.
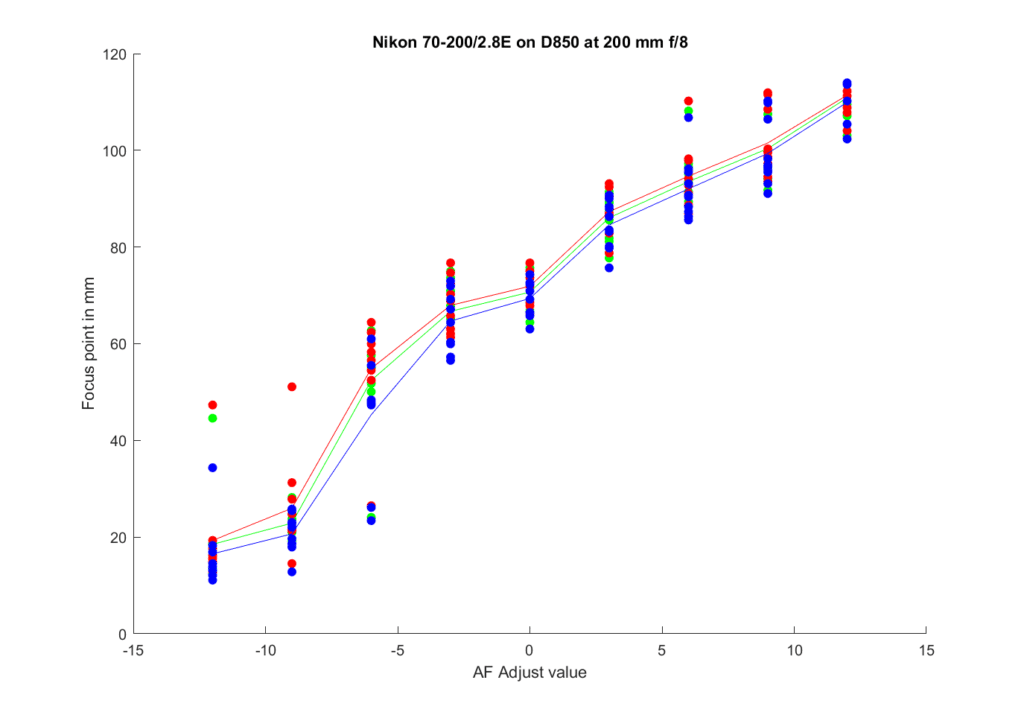
Here’s what I got for the green channel:
I apologize for the different vertical axes for my f/2.8 and f/8 plots. the span of the one about is 120 mm and the f/2.8 plot’s span was 160 mm. The amount of shift distance is about the same in the two plots, as I’d expect. The scatter is also about the same.
For completeness, here are all three color channels:
I call this a good beginning. Next, I’ll try to teach my code some trick that FocusTune doesn’t know so that I can look directly at focus shift vs f-stop.
Jim, do you know how sensitive Brenner’s method (or other focus measure functions) are to slight changes? I’ve noticed that when using FocusTune, if there are slight shifts, like on the order of 1mm, of where on the target the camera is pointing, the results aren’t really comparable. Also if it’s overly sensitive, it may be responding to other factors that aren’t being measured.
For example, I shoot a series at 5-point AF tune intervals for the full range of adjustments (ie. 0, +5, +10, …, -5, -10, etc.), and then shoot 1-point intervals around the area which crosses the X-axis to find the closest AF tune number. When I use both data sets in the same director for Focustune, the 1-point numbers tend to be shifted as a whole relative to the 5-point numbers. But when I analyze them separately, the AF tune number they predict seem to be more in line with the 5-point series.
The reason there’s a slight shift in my setup is because my tripod (an RRS TVC-34) is on carpet, and I think just the act of removing and inserting the memory card in between the 5- and 1-point runs is enough to shift the camera slightly.
I also wonder how the focus measure functions react to lens aberrations, which may be important since some lenses clean up quite a bit when they’re stopped down.
With the LensAlign ramp, Brenner’s method results in a measure that has periodic variations. That’s because the pattern spans several pixels, and as you track over it at one-pixel intervals, you’re seeing different parts of the pattern. I deal with that by applying a smoothing function. Choosing the right function is somewhat of an art, and I look at the smoothed and raw plots for each data point to make sure there’s nothing wonky. Once I get more confidence, I’ll stop doing that. I don’t know how FocusTune smooths, but I’m pretty sure they have to do so.
WRT the carpet, I think that’s a bad idea. I use vinyl tile on a concrete floor.
If you’re worried about the memory card, have you considered shooting tethered? But I think you could do your runs at 4-step intervals and interpolate, and dispense with the 1-step runs entirely.
Here’s some comfort. The shot to shot variations of PDAF are so great that I think it’s futile to try to get the AF adjustment to within one integer difference of some theoretical perfection. When I worked at IBM, the folks had a phrase for that, which I won’t repeat, but it started “polishing a…”