You can do the test perfectly well without understanding why it works, but knowing what’s behind it may make the whole procedure make more sense to you.
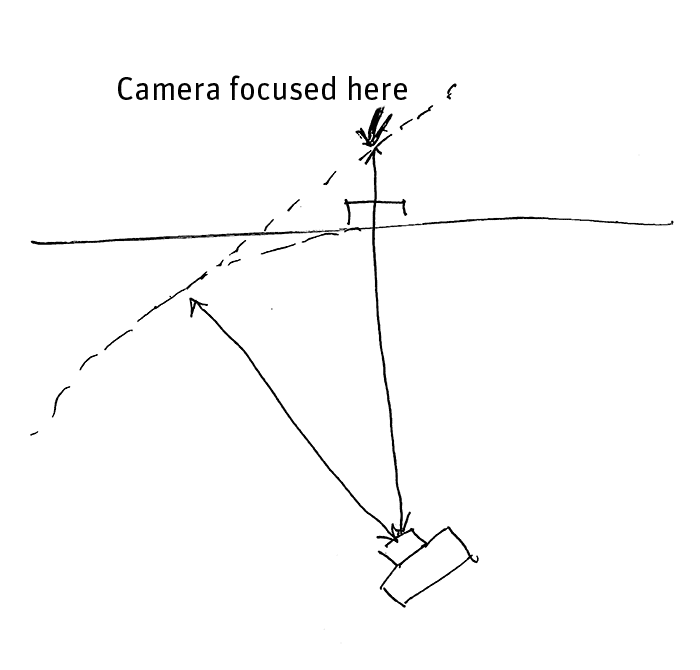
The basic idea is to focus with the target in the center of the image, then recompose so that the target is in the four corners of the image and optionally, at the middle of each edge, then compare sharpness.
But you have to be far enough away from the target. Here’s why.
Above is a crude diagram looking down with one target on-axis and one at the far right edge of the image. Because we’re assuming a rectilinear lens, in which straight lines in the image map to straight lines on the sensor, both targets are in focus. But what happens if we dispense with the second target, and skew the lens so that the first one is at the same place in the image?
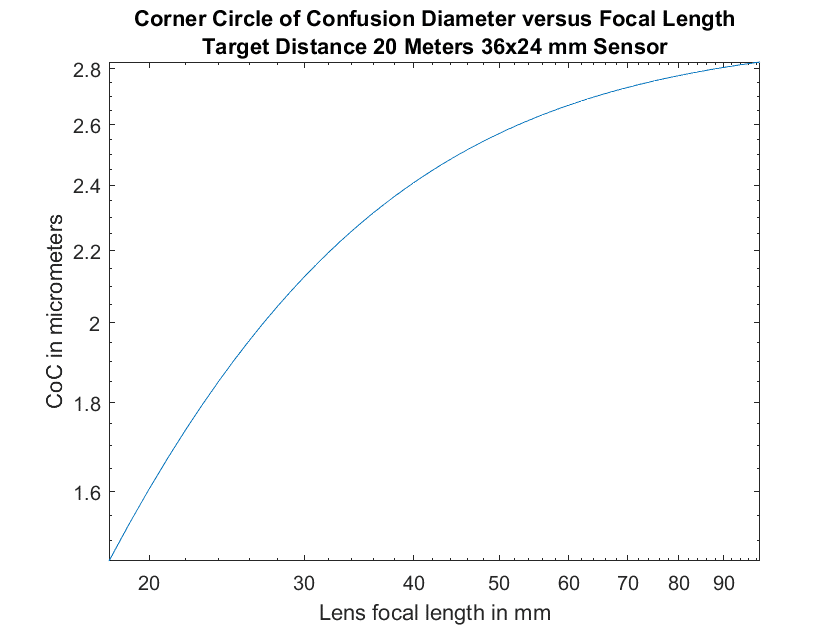
Now the target is out of focus. Specifically, it’s too close. This isn’t a problem at extreme distances. Infinity is infinity no matter where in the frame it is. Depth of field (DOF) can cover up this focusing error. In order to put some numbers on it, I wrote a computer program to compute the diameter of the circle of confusion (CoC) for this kind of misfocus at the very corner of the sensor for lenses between 18 and 100 mm on a full frame (FF, 24×36 mm)) sensor at f/4 with a target distance of 20 meters.
We’d like the CoC to be quite a bit smaller than the pixel pitch. FF cameras of high resolution have pixel pitches on the order of 4.5 micrometers (um). Halving the CoC half that should be good enough. You can see from the above graph that we’re in good shape at 20 meters for lenses up to about 35 mm, but that beyond that, we need to be further away.
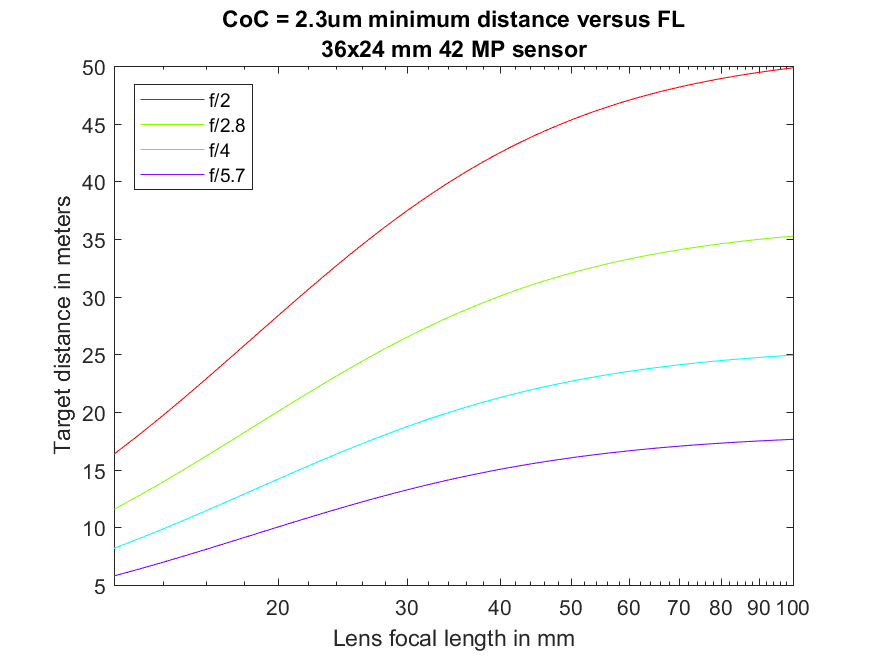
I created a set of curves that show the distance required for a 2.25 um CoC diameter for a full frame, 4.5 um camera for focal lengths between 12 mm and 100 mm.
This show you how far you need to be from the target. You can be farther than that without causing problems as long as your target is big enough on the sensor and there’s not so much air between the camera and the target that atmospheric effects are important. Stay under 200 meters, and you should be fine unless you’re shooting over heat sources.
I’ve prepared versions of the above chart for MFT, APS-C, full frame, and 33×44 mm sensors, for three ranges of focal lengths. You can find them here.