There are several steps in getting to the JPEG preview image in a raw file. All of them except the last step, compression, apply to the in-camera histogram. For the purpose of this paper, I’ll assume that the compression/reconstruction process is lossless. It is not, but the lossy nature of the process does not affect the in-camera histogram in any material way.
The raw image. The sensor in the camera is covered with a color filter array, which allows three colors of light to fall on the photosensitive sites, one color per site. The arrangement of the CFA is usually in a Bayer Pattern, named after, Bruce Bayer, who worked for Eastman Kodak in 1976 when he invented the pattern. The Bayer Pattern has twice as many green as red or blue filters, on the quite accurate assumption that the human eye is more sensitive to fine detail in luminance than chrominance, and that the principle carrier of luminance information is the green pixels. On the camera sensor, the red pixels have no blue or green components, the green pixels have no red or blue components, and the blue pixels have no red or green components. This information constitutes the bulk of the raw file. The gamma is one, which is another way of saying that the image is in a linear color space. There are exceptions to the previous sentence; in the NEX-7, and reportedly in the RX-1, Sony applies a curve to the linear values and quantizes them to eight bits per primary.
Demosaicing. The first step in our chain is creating an image with red, green, and blue values for every pixel in the image. Demosaicing consists of creating the missing components for each pixel. There are many ways to do that; if you have a background in image processing, you might want to take a look at this survey article. The simplest way to create the missing information is to interpolate the missing green information from the nearby green pixels, the missing blue information from the nearby blue pixels, and the missing red information from the nearby red pixels. Thus, two-thirds of the color information in a raw image is made up. After demosaicing, we have a full-resolution image in the native color space of the camera.
Conversion to a standard color space. It is possible to exactly convert a linear RGB representation of an image to standard colorimetric color space like sRGB, Adobe (1998) RGB, or ProPhoto RGB if and only if the spectral sensitivities of the three camera primaries are a three-by-three matrix multiplication away from CIE 1931 XYZ. This is my specialized restatement of what color scientists call the Luther-Ives condition. There are some excellent reasons why the spectral sensitivities of the filters in the Bayer Array on your camera don’t meet the Luther-Ives condition. Those reasons include a desire to maximize the signal-to-noise ratio in the image and have a high ISO rating, and limitations in available dyes.
Because the filters in the Bayer Array of your camera don’t meet the Luther-Ives condition, there are some spectra that your eyes see as matching, and the camera sees as different, and there are some spectra that the camera sees as matching and your eyes see as different. This is called camera metamerism. No amount of post-exposure processing can fix this.
Camera manufacturers and raw developer application writers generally use a compromise three-by-three matrix intended to minimize color errors for common objects lit by common light sources, and multiply the RGB values in the demosaiced image by this matrix as if Luther-Ives were met to get to some a linear variant of a standard color space like sRGB or Adobe (1998) RGB. There are ways to get more accurate color, such as three-dimensional lookup tables, but they are memory and computation intensive and are not generally used in cameras.
The next step is to perform white balancing. There are lots of ways to do that, and some are more accurate than others. A fairly crude, but effective, technique is usually used in cameras: multiplying each pixel value by a diagonal matrix as follows:
The green coefficient, Wg, is usually one, and the red and blue coefficients define the neutral axis of the image.
In addition, the cameras apply contrast adjustment, brightening or darkening, and sharpening to the image. Some or all of the above mathematical operations can be combined to make the processing simpler, but if you’re a user, it’s best to think of them separately.
The final step is to apply a tone curve to the data in each of the primaries. This curve is usually identified by the parameter “gamma”. How this set of curves came to be first a de facto, and now a de jure standard for RGB color spaces is a tale rooted in the physics of cathode ray tubes. , the computer image display characteristic that gives the now standardized gammas that we use is not the result of optimization for human vision, but the result of a happy accident that characterizes the relationship between the number of electrons impinging on a cathode ray tube phosphor and the number of photons coming out. The peculiar genesis of correction for CRT nonlinearities is the reason that the file gammas of RGB images are expressed “backwards”. The power law that encodes a linear representation of the scene into a “gamma 2.2” file is .45, the inverse of what you would think it would be. The way to correctly, if longwindedly, state the characteristics of a gamma 2.2 encoding is to say that the file is encoded for a display that has a gamma of 2.2.
Next: Making the in-camera histogram closely represent the raw histogram
ted says
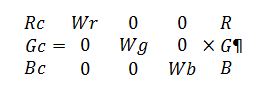
Like your blog.
I might suggest its misleading to refer to the gamma encoding as a tone curve, because the net effect should be no tonal adjustment at all. e.g. consider if gamma encoding was not used and display had a linear response for voltage versus photon emitted, then the image would appear identical to one where that was gamma encoded using .45 and displayed on a “CRT” with a gamma of 2.2.
There is often an additional tonal curve applied to make the image display better at the luminescence levels expected of the display but that is something different.
JimK says
I see your point, but that is the common usage in the color science biz.
David Clark says
The link in this article is broken. Is it possible to get a link that works?
JimK says
Sorry, no. I will remove the broken link.
sashi daniels says
Interesting…that bit about CRT. I would like to add a bit, if I may. I used to work on CRT monitors and considered images when viewed on LCD monitors, when newly introduced, as having jagged edges and the colors were different. Today I use a 4K monitor and do not notice any jagged edges–a testament to how the human eye and brain adjusts. I still own a CRT monitors because, in the first place, I started with mono CRT (developed my first brochure on mono CRT using Corel 3, and CYMK values), and then on to color CRTs when they became popular and affordable (here in India, when first introduced, CRTs cost as much as Rs 100,000 back in the early 90s). It is not just the color of CRTs that I still admire, but, being an electronics hobbyist, I am still in awe at the stupendous background technology in the CRT itself, the controlling yoke, and the circuitry. A pity CRTs died. BTW I did not have much of a problem with on screen color and print results match.