FF examples of optimal blur management

This is a continuation of a series of posts about blur management for landscape photography. The series starts here.

In a previous post, I showed you the results of using a blur management optimizer that I wrote on a scene using the Fuji GFX 50R. This post uses different scenes, the Nikon Z7 body, and the Nikon 14-30 mm f/4 lens . I measured object distances in meters (with a Nikon Aculon laser rangefinder) and have overlaid them on the objects in the images. I will show you the weightings that I used and the results. I will also show you weightings from an experienced landscape photographer who just eyeballed the images (with the distances overlaid), and from another such person who used an iPhone app called TrueDOF-Pro, which takes both diffraction and defocus blur into account, but not sensor pixel blur. And finally, I’ll show what happens when you use a variant of a common object-space DOF technique: set the focal distance to the farthest object and adjust the aperture for acceptable defocus blur in the foreground. I used 30 um as the threshold of acceptability.

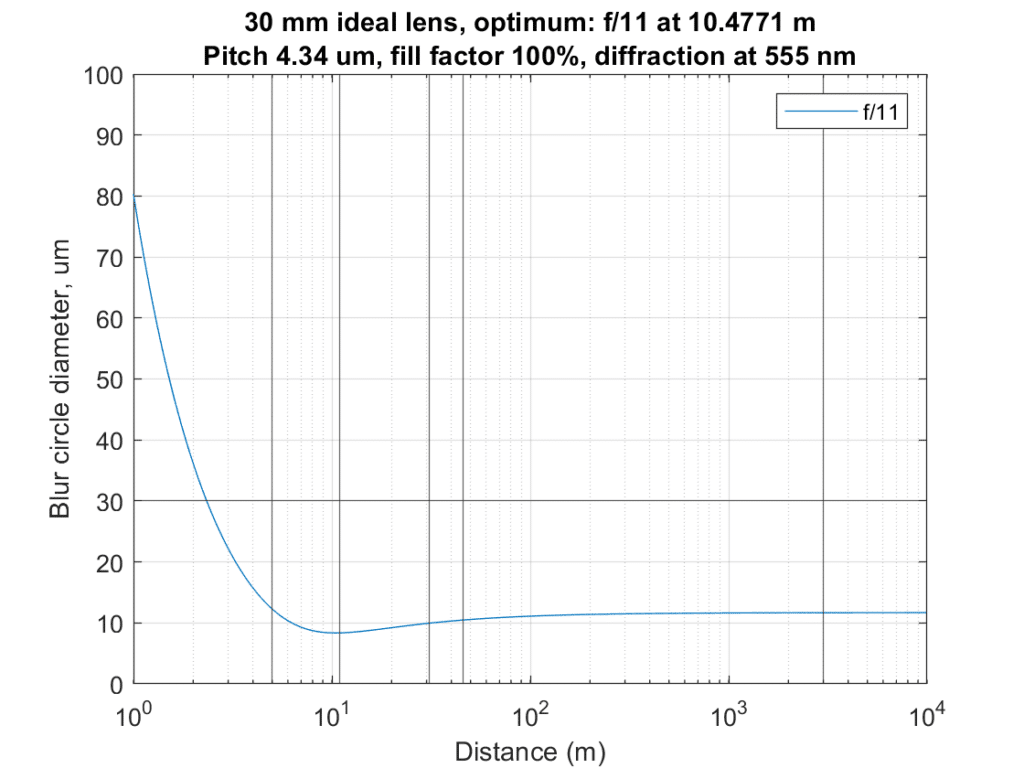
Here’s the first scene, with the lens set to 30 mm:

Here are the weightings that I used:

subjectDistances = [5 11 31 46 3000]; %case 1
subjectWeights = [1.5 1 1 1 1]; %case 1

And this is the result:

 

Worst-case blur is about 13 um. The distant hills have about the same blur — call it 12 um.

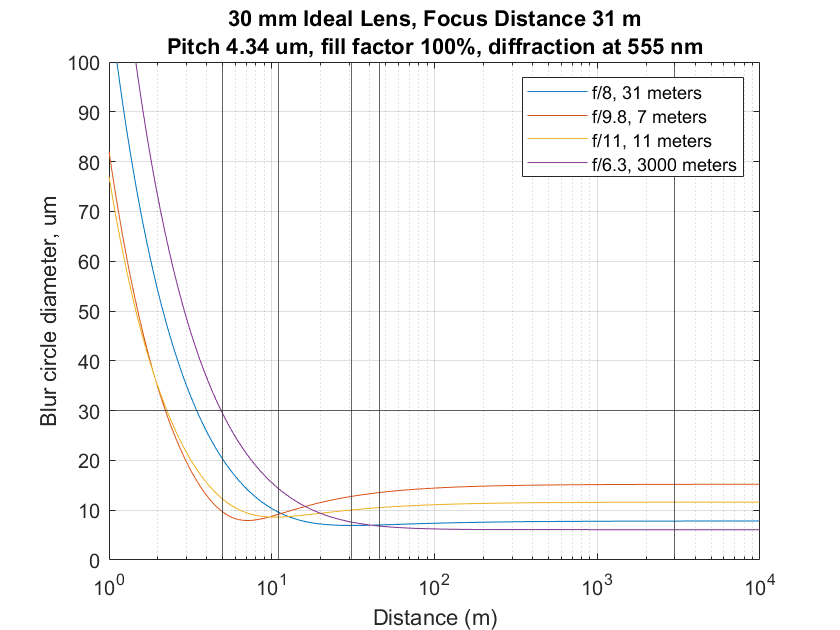
Now I’ll plot the other three results and the above ones on the same graph:

The blue curve is the seat-of-the-pants one, the red is from the TrueDOF-Pro user, the yellow is from my optimizer, and the purple is the far-object method. When compared to my optimizer, the TrueDOF method achieved sharp results for the two closest objects — the object positions are marked with vertical black lines — but sacrificed the distant ones. Both the other methods resulted in a fuzzy nearest objects, but slightly sharper distant ones.

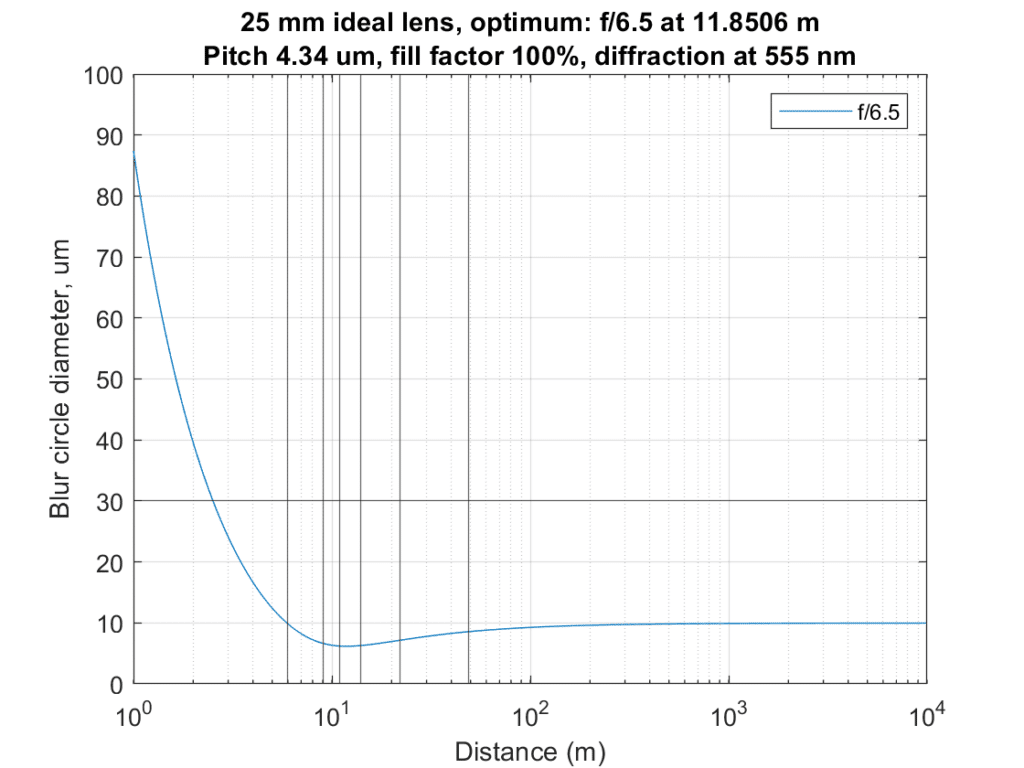
Now with the lens set to 25 mm:

My weights:

subjectDistances = [6 9 14 22 11 49]; %case 2
subjectWeights = [1 1 1 1 1 1]; %case 2

The optimizer results:

 

10 um blur circles or less for all objects.

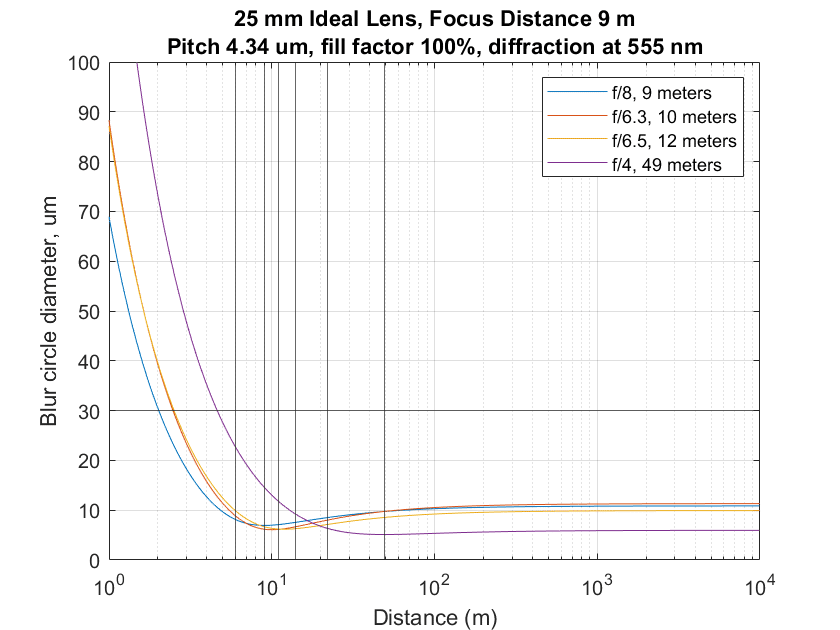
The other approaches, with the curves the same colors as above:

Everyone is in the same ballpark except the distant-object approach.

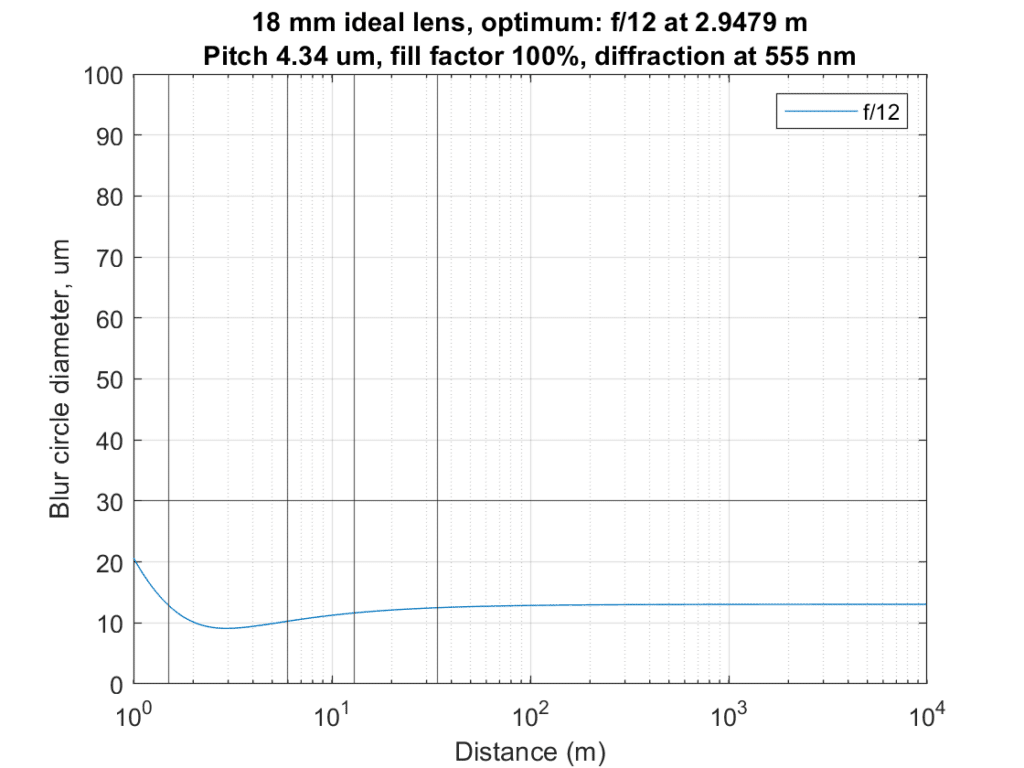
Now with the lens set to 18 mm:

Weights:

subjectDistances = [1.5 6 13 34]; %case 3
subjectWeights = [1.5 1 1 1]; %case 3

Optimizer results:

 

13 um or better for all the objects.

Other approaches:

The eyeball and optimizer curves are on top of each other. Both the other curves sacrifice the foreground. The TrueDOF calculator would presumably given something like the results of the optimizer if the user hadn’t given up on the nearest object.

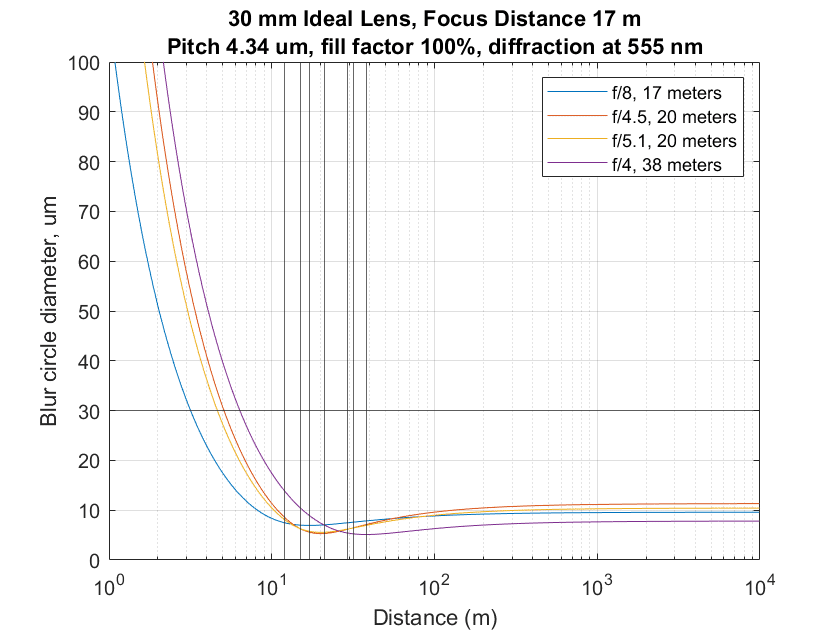
Next, with a 30 mm setting:

 

Weights:

subjectDistances = [12 15 17 21 29 32 38]; %case 4
subjectWeights = [1 1 1 1 1 1 1 ]; %case 4

Optimizer results:

This is a pretty easy situation. All blur circles are less than about 8 um in diameter.

The other approaches:

All about the same except for focus on the far.

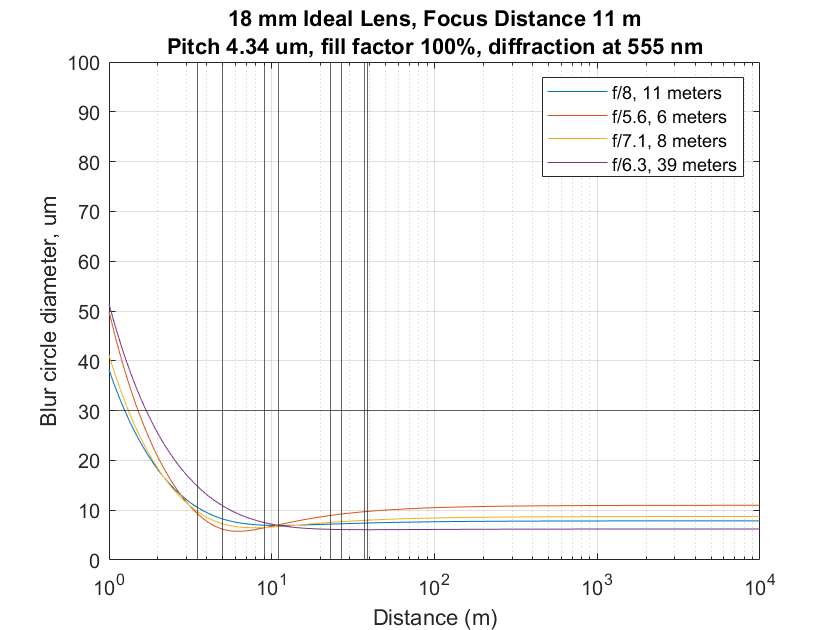
With the lens set to 18 mm:

Weights:

subjectDistances = [3.5 5 9 11 23 27 37 39 ]; %case 5
subjectWeights = [1.5 1 1 1 1 1 1 1]; %case 5

Optimizer solution:

 

Less than 10 um CoCs for all the objects.

The other approaches:

The eyeball method and the optimizer are close. TrueDOF sacrifices distance sharpness for moderate foreground gains. Far-focusing has the best distance sharpness, but the foreground is the softest.

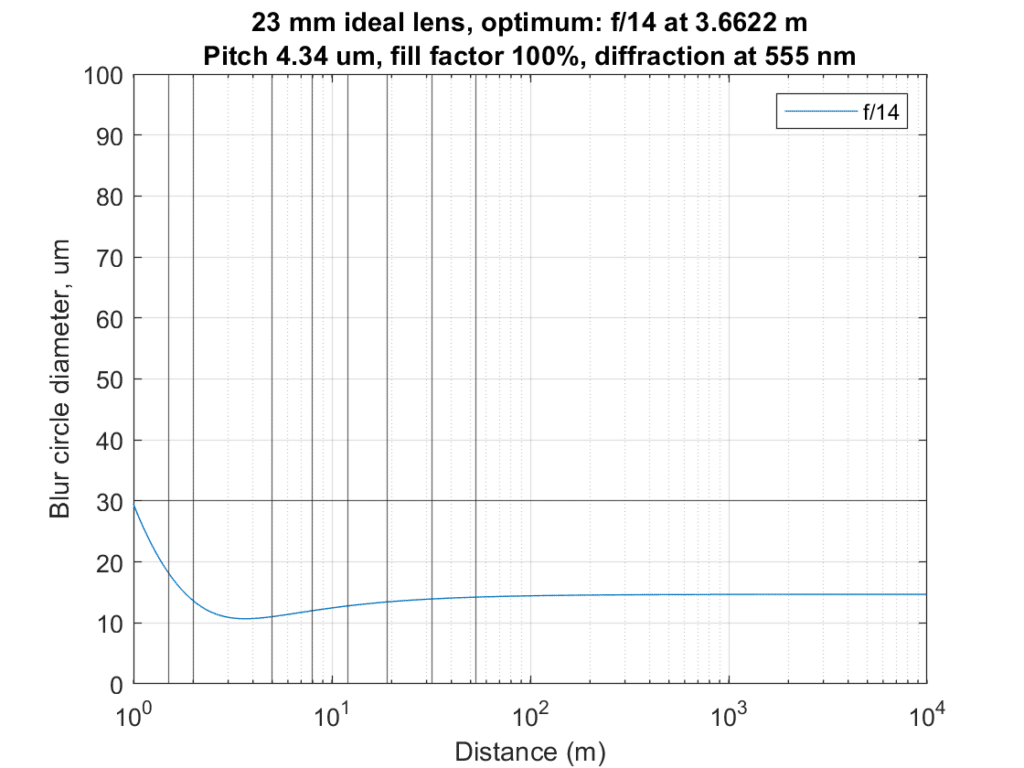
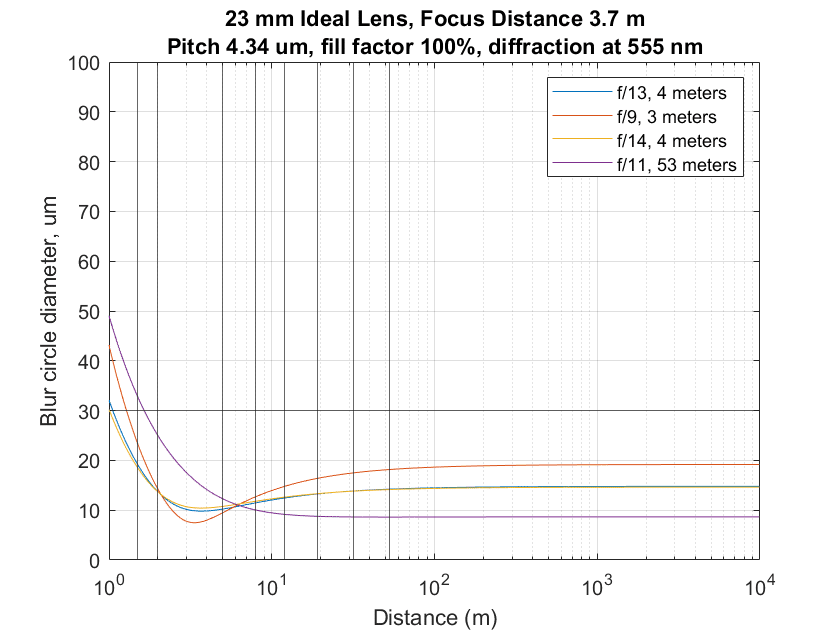
And finally, with a 23 mm lens setting:

Weights:

subjectDistances = [1.5 2 5 8 12 19 32 53 ]; %case 6
subjectWeights = [1.5 1 1 1 1 1 1 1]; %case 6

Optimizer results:

18 mm CoC for the nearest object, and less than 15 um for everything else.

The other approaches:

The seat of the pants solution and the optimizer one are essentially the same. The TrueDOF solution sacrifices in both the near and the far without much improvement in the middle. The focus on the far method has the worst foreground blur, but significantly sharper distant objects.