This is a continuation of a series of posts about blur management for landscape photography. The series starts here. This is quite a nerdy little post. If you aren’t interested in the mathematical details behind deciding the best way to manage blur you should probably move on.
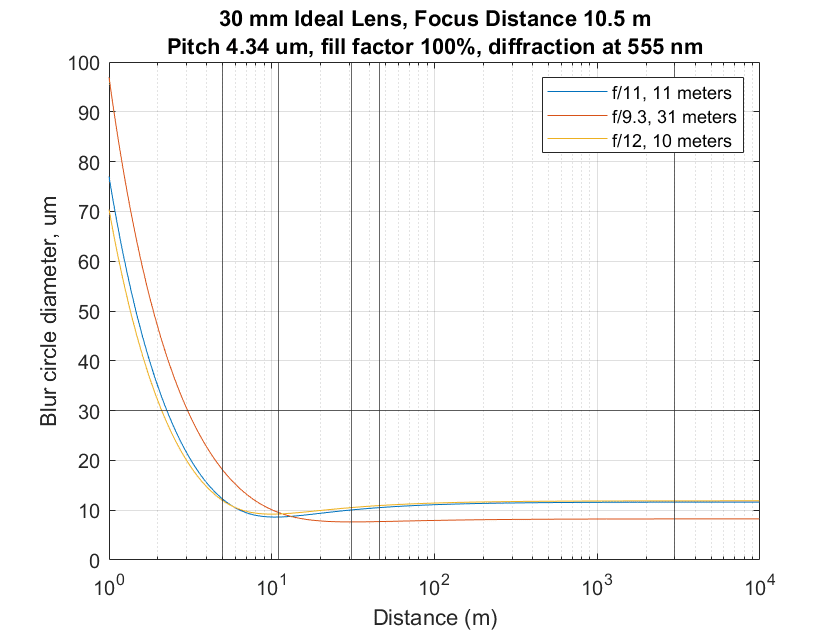
To search for an optimum solution to a problem, you need to define a scalar (one-dimensional) metric of goodness or badness. You can maximize the goodness, or minimize the badness. When I set up the blur optimizer, I picked two such metrics, the diameter of the circle of confusion (CoC), and the number of those CoCs per picture height. The first is a measure of badness, and I’ve been posting solutions that minimize it. The second is a goodness assessment, and I haven’t posted any results that use that.
But there’s another set of decisions to me made: how the contributions to fuzziness (CoC diameter) or sharpness (CoCs/ph) are to be aggregated with respect to the distances and the weights. In everything I’ve posted so far, the diameters at each distance have been squared, then multiplied by the weights, then summed. This is the so-called “sum of squares” conversion from vector to scalar that I usually employ when I have no reason to do otherwise.
Sum of squares weights the worst cases more than better ones. I’ve noticed that in the solutions I’ve posted. But there are other, perfectly reasonable, ways of adding up the errors at the selected distances. One is to do a simple weighted sum: weight the blur diameters at each distance by the assigned weight, then just add ’em up. There’s an even simpler approach: ignore the weight, and simply minimize the worst-case blur diameter.
In this post, I’m going to show you what happens when all three are applied to an image. It’s one you’ve seen before if you’ve been following along in this series.
Distances in meters are labeled in red. Focal length was 30 mm . Camera was a Nikon Z7, and I used the Nikon 14-30 mm f/4 zoom.
Here are the results of all three methods:
The blue curve is the one you’ve seen before. I got to that with the sum of squares approach. The red curve is the result of choosing a simple weighted sum. You can see that it is significantly more distant in its choice of where to focus, and slightly more aggressive about opening up to avoid diffraction. The yellow worst-case results are very similar to the sum of squares ones.
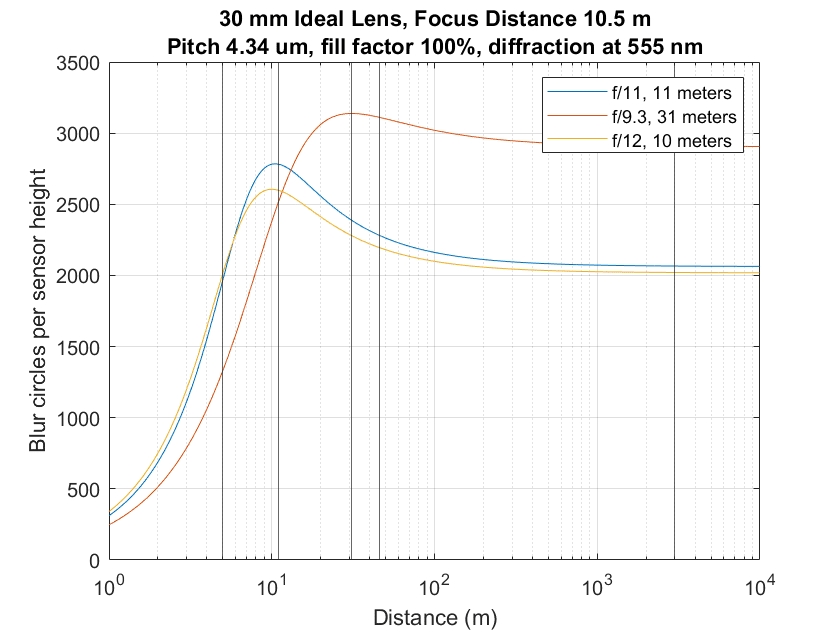
If we flip the graphs over and look at a sharpness metric, the differences where the CoCs are small become more apparent, and the deltas when the CoCs are large get visually smaller.
What’s the right answer? Depends on your objectives. I’m thinking about exploring exponents between 1 and 2.

Leave a Reply