Gamut of a basis-function derived metamer set

I’ve previously reported on a project about observer metameric errors in digital cameras. I built a program that, given a target color and a set of sample reflectance spectra, will:

1. Using principal component analysis, find a set of basis functions for the sample set
2. Assuming the set is lit with a particular illuminant (I used D50 for the data I’m presenting here), find as many spectra as you specify by combining the basis functions.
3. All of the spectra will resolve to the same color for a CIE 1931 2-degre observer. They are therefore metamers.
4. I set the boundary conditions to exclude spectra with over 100% or less than 0%  reflectance

I’ve showed you some of the results, and I’ll be showing you more, but I decided before going too much further, I wanted to learn something about the metamer sets themselves. I was particularly concerned about their gamut.

I beavered away at some Matlab programming, including parallelizing the code so that it would produce results this year (OK, that’s an exaggeration). Here’s what I got this morning:

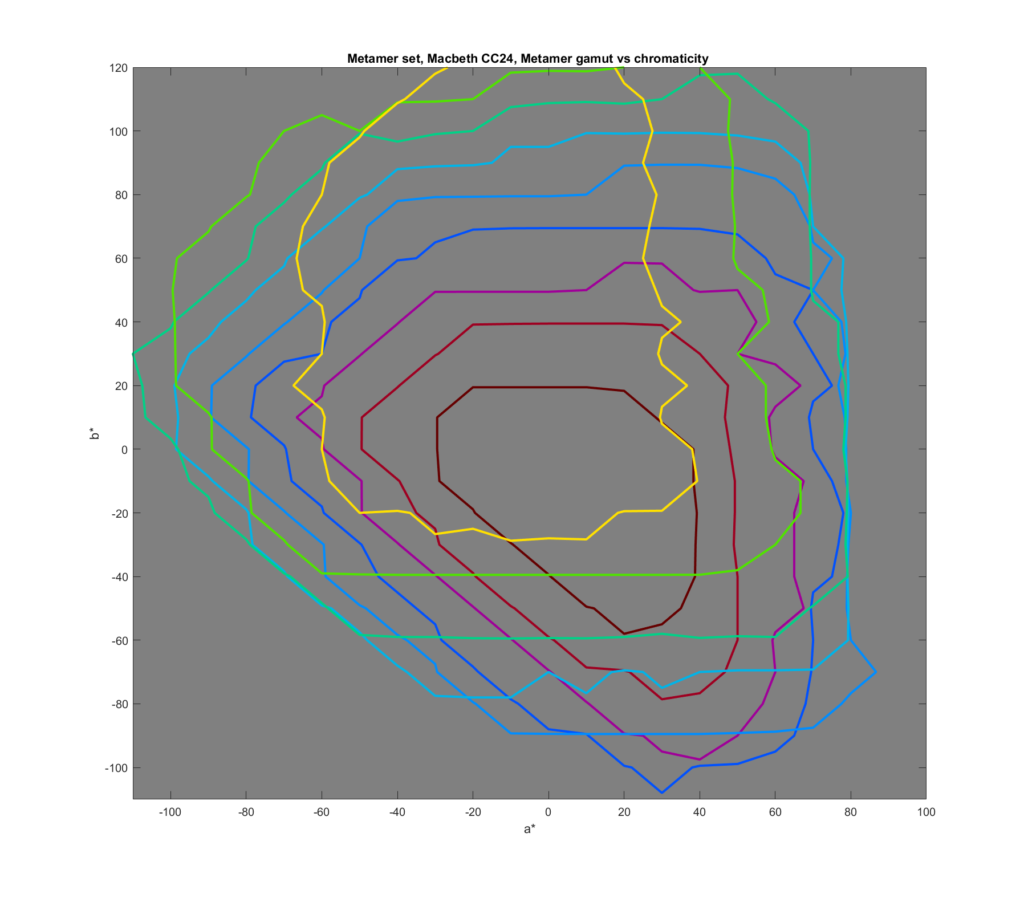
This is a contour plot, looking at the CIEL*a*b* chromaticity plane. Nine L* values are calculated, for L* = 10 through L* = 90 in steps of 10. The luminance of the lines is approximately that of the L* to which they correspond. The hue angle changes 40 degrees clockwise with each L* step, starting at 45 degrees and ending at 85 degrees. The source for the basis functions was the Macbeth CC24 chart. I used the 7 most significant basis functions.

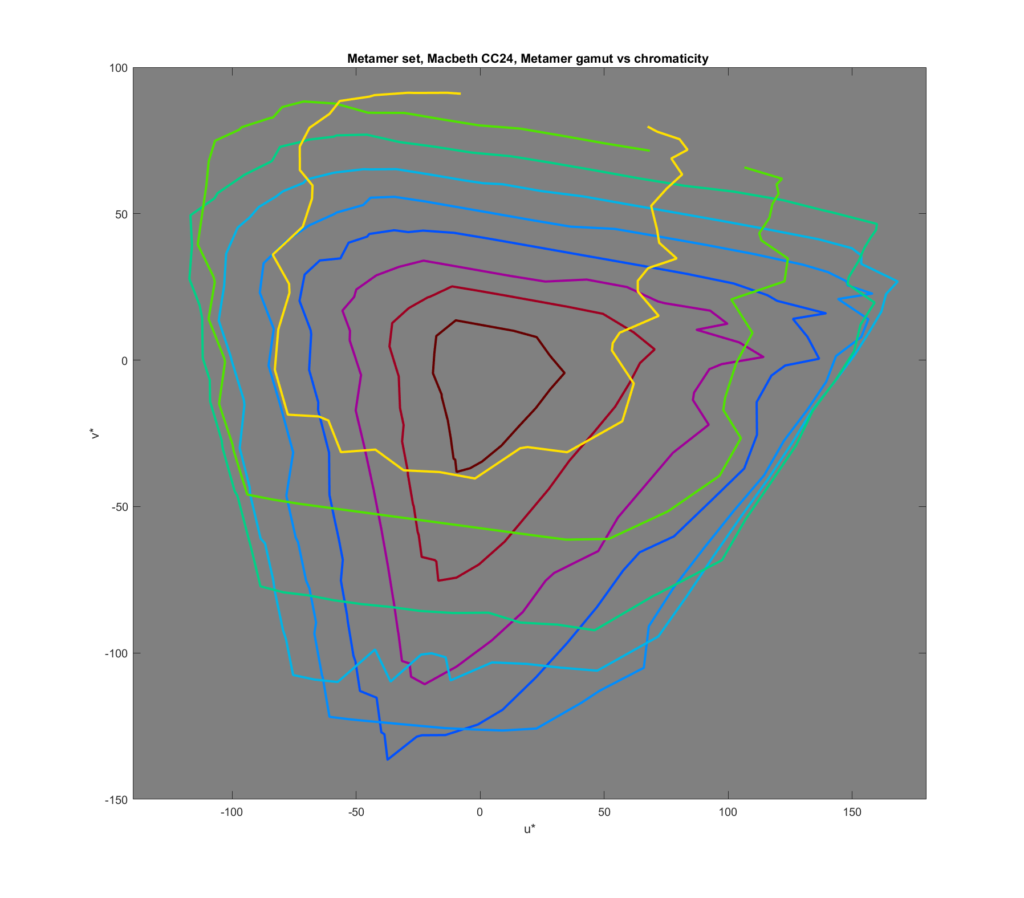
Here’s the same data in CIEL*u*v*:

In case you’re asking  yourself, “How can he get away with converting the Lab data to Luv if the testing was done in Lab?”, let me offer this: both Lab and Luv are based upon CIE XYZ. There are several color matching functions for XYZ, from the 1931 one to one in the early 2000s. So pick any one for the comparison, and use it for both Lab and Luv. Then, spectra that are metamers in Lab must perforce be metamers in Luv, even though they may resolve to wildly different triplets (well, doublets, since the L* will be the same) in each space.

Whether looks at in Lab or Luv, I was surprised that the gamut was so large.