This is one in a series of posts on the Fujifilm GFX 100S. You should be able to find all the posts about that camera in the Category List on the right sidebar, below the Articles widget. There’s a drop-down menu there that you can use to get to all the posts in this series; just look for “GFX 100S”.
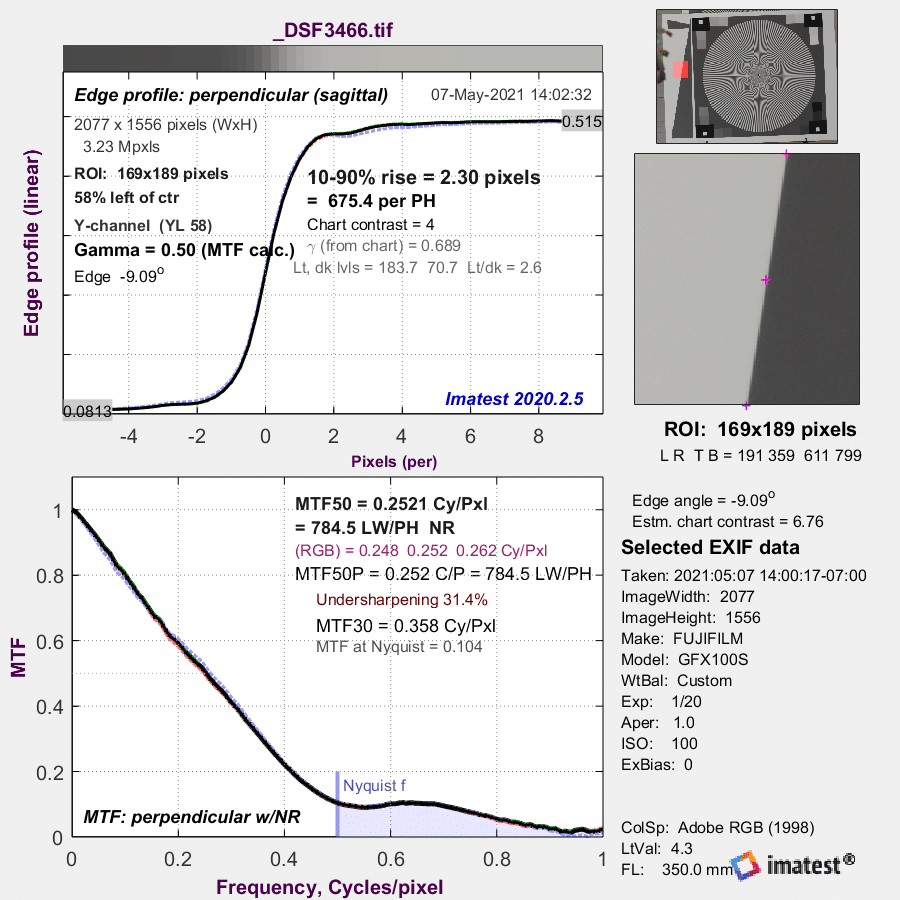
Yesterday, I published an MTF curve for the Rodenstock 180 mm f/5.6 HR Digaron S on the Fuji GFX 100S. To refresh your memory, here it is:
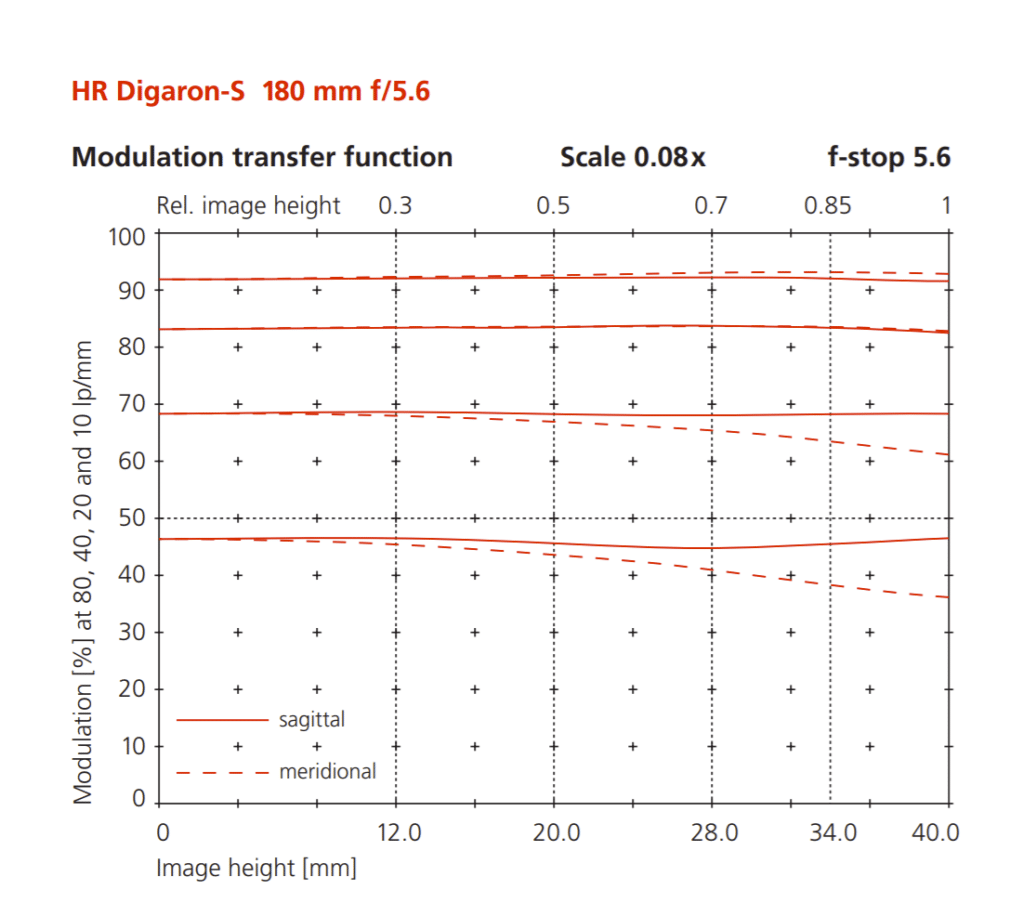
Rodenstock publishes MTF data for that lens, and Rodenstock is one of the few that measure that data from real lenses, rather than using a simulator to get it:
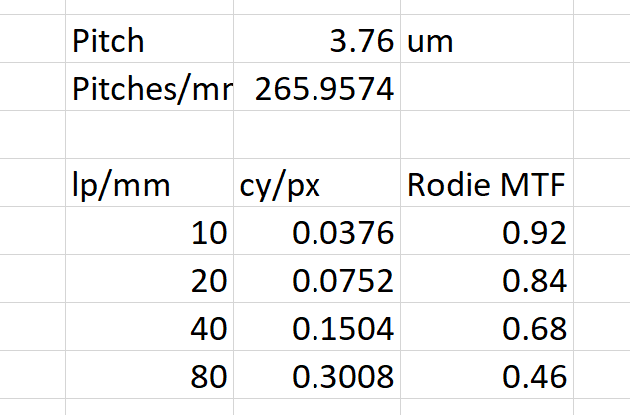
My MTF testing was done very close to the axis, so if we want to compare the two measurements, we can look at the places on the Rodenstock curves where the different frequency curves intercept the y-axis. Sagittal and meridional numbers are the same there, so we just have four numbers to plot. But we have to convert the frequencies from line pairs per mm (which is close enough to cycles/mm for this work) to cycles/pixel. We know the pitch of the GFX 100S is 3.76 um, so this table will do the conversion for us:
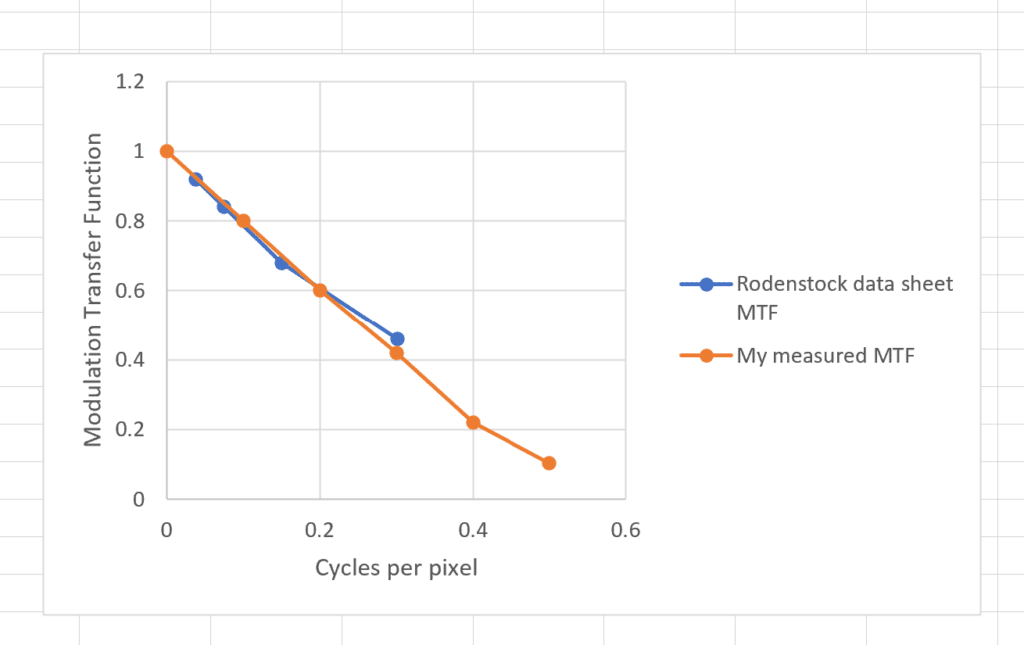
Plotting both sets of curves on the same graph, we get this:
Agreement is surprisingly good — at least, I was surprised. How can this be? My measured data is degraded by the effective pixel aperture of the GFX 100S, and the Rodenstock data is measured directly at the focal plane.
The answer lies in where the Rodenstock data stops in terms of frequency. The highest frequency is 80 lp/mm, which is about 0.3 cycles per pixel, which is just about where the pixel aperture size starts to become material. I may be reading too much into small differences, but I note that is the place where the two curves start to diverge.
Thanks to Erik for the idea to do this presentation, and for his cut at using the same data for comparison.
The published MTF curve follows REALLY closely the diffraction-bound MTF curve with the cut-off at 1 cycle/5.5 μm. With ƒ/5.6, this corresponds to wavelength 0.49μm.
I wonder what was the color temperature of their light source…
P.S. BTW, since indeed this confirms that (there are cases when) the Imatest’s MTF curve is reasonable, I need to recheck my methodology. However, I hesitate with repeating the manual digitization of the edge curve.
I’m quite sure that it is possible to ask Imatest to convert the edge profile to a CSV file. May I ask you to post these values for Rodenstock?
Its really nice to see a company publish specifications for their products that can actually be independently verified, in particular without expensive test equipment.
What an absurdly sharp lens.
I wonder how it would do on the LensRentals test bench (they did a test up to 240 lp/mm and none of the lenses they tested, which were all for 35mm except the Canon tilt-shift 90mm).
Oops, I accidentally a clause.
And none of the lenses they tested had anywhere near the consistent cross-frame sharpness at 80ish lp/mm like this.
• Consistency is overrated. Did you notice much higher resolution in the center in Lensrental’s tests?! (Due to f/4 they used.)
• LR did not text anything above 135 mm (and in their tests 135 mm behave much better than the rest!). (However, 180 mm @ 40 mm-away is harder to implement than 135 mm @ 20 mm away!)
So while this IS an amazing lens, it is not 4 steps ahead – only about 2 steps ahead! 😉
It would be very interesting to see the same comparison for the edges of the frame (radial and sagittal values for the far right and left of the frame).
Contrary to what Ilya stated LR do occasionally test longer lenses, up to 400 mm.
In his article “Supertelephoto MTF Curves” Roger concluded that no copy of the lenses they tested approached the published MTF.
Rodagon supplied values seem optimistic too, especially for 80 lp. None of the top lenses tested by LR in their “Experiments For Ultra High Resolution Camera Sensors” and “More Ultra High-Resolution MTF Experiments” equaled the 45% value for the points 20 mm from the center given for Digaron, even though they were constructed for much smaller frame. None of them even equaled the value given by Rodagon for the edge of 6×6 frame (above 40 %). And none of them approached the flatness of Digaron’s curves.