Radial and tangential edges and blur

This is one in a series of posts on the Fujifilm GFX 100S. You should be able to find all the posts about that camera in the Category List on the right sidebar, below the Articles widget. There’s a drop-down menu there that you can use to get to all the posts in this series; just look for “GFX 100S”. Since it’s more about the lenses than the camera, I’m also tagging it with the other Fuji GFX tags.

There has been some confusion about the directions that I’ve been using in my off-axis testing of the Fuji GF lenses. I sympathize; the topic is inherently confusing on several levels. I’ll try to peel that onion for you.

The first step is to understand what I mean by radial and tangential directions. I am using those terms because, in a well-constructed lens, lens aberrations have radial symmetry, or symmetry in which the aberrations exhibit correspondence or regularity  around a central axis in the center of the image. I’ve drawn lines in the radial direction on the image below (made with the 23 mm f/4 GF lens).

Now here are lines in the tangential direction:

If we refer to the edges in the slanted edge figure in the target, we can see that one of them is more-or-less in the tangential direction, and the other is mostly in the radial direction (they’re not exactly in those directions because they need to be a little off to make the slanted edge technique work). I’ve labeled the edges on the drawing below:

And that’s all you need to understand the testing I’ve reported on so far. However, there is one more layer of complexity to peel away. The slanted edge method measures the blur perpendicular to the edge being analyzed. So the tangential edge is used to measure radial blur, and the radial edge is used to measure tangential blur. I’ve marked the edges appropriately below:

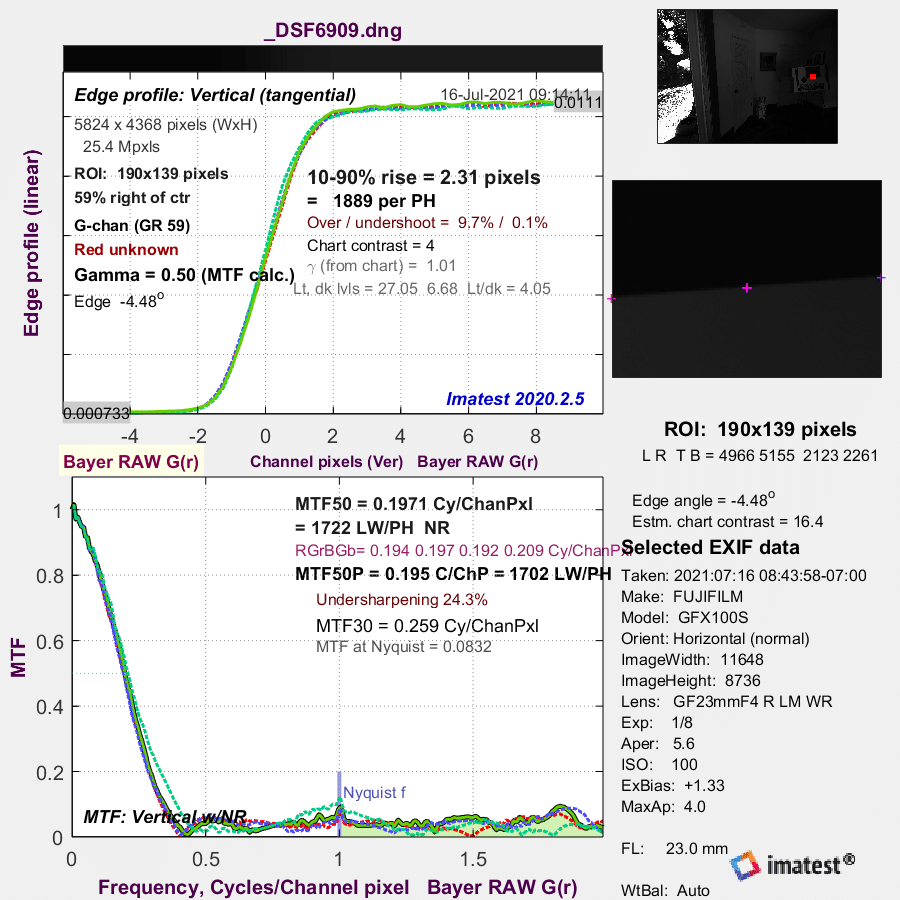
In lens testing, the usual convention is to talk about the direction of the blur rather than the direction of the edge. Here is an Imatest analysis of the radial edge in the above image:

Note that it says the edge profile is tangential. And, if you understand what they’re doing, it makes sense. They are analyzing the profile of the edge perpendicular to the direction of the edge itself. In the nomenclature that I’m describing, radial is perpendicular to tangential.

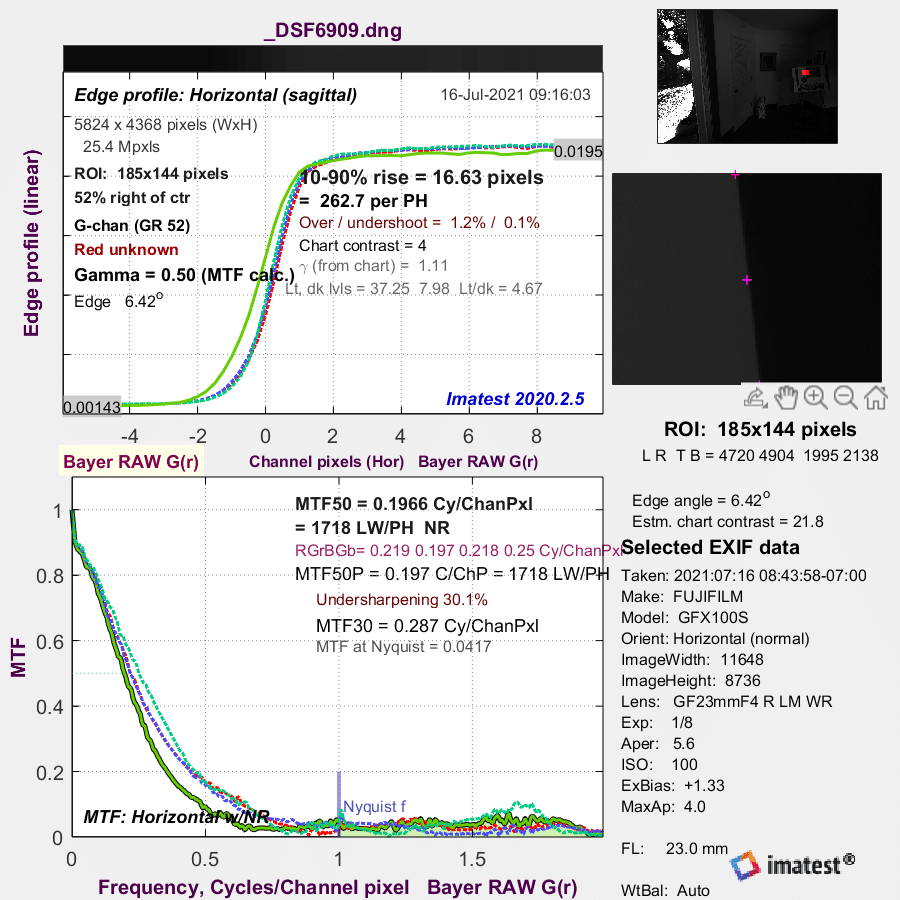
Here’s what Imatest has to say about the tangential edge:

Wait, what? It’s calling that profile sagittal! In this context, sagittal is another name for radial.