In 1991, I noted the phenomenon that Wells calls combing, came up with a few ways to artfully trade off image resolution for reduction or elimination of the effect, and submitted a patent disclosure to my employer. They weren’t interested in patenting the ideas, but instead published it in order to keep anyone else from patenting them.
In those days images were coded with far less precision than today. We will see in the next post how that makes a huge difference.
In the processing of photographic or photorealistic images, the image information is usually represented in fixed point form, using a number of bits for each color plane (or for the greyscale information, in the case of a monochromatic image) that is adequate for sufficiently accurate representation of the image information in the final form. In the nineties and early years of this millennium, monochromatic images were often represented using one byte (eight bits) per pixel, allowing the representation of 256 shades of grey, barely enough to prevent visible banding or contouring in image areas with high energy at low spatial frequencies and low energies at high spatial frequencies. Color images were often represented using three bytes per pixel, one byte for each color plane.
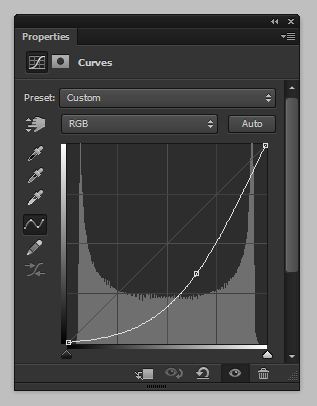
Many operations in image processing involve subjecting every pixel in the image to computational process to produce a new value for that pixel. If, for every pixel in the image, only that pixel and the algorithm influence the result, this kind of processing as called point processing, and the algorithm is referred to as a point process. An example of a point process is changing the brightness of an image through the levels or curves tools. In the case of a monochromatic image represented with one byte per pixel, lowering the brightness of an image without changing either the white or black points using conventional methods involves passing every pixel in the image through an algorithm with a transfer function similar to one shown below.
Such a function has a slope of less than unity for dark pixels, and a slope of greater than one for bright pixels. For the dark pixels, there will be more than one input value mapped to some output values, and for the light pixels, there will be some values which are not present in the output image, no matter what the input values. Consider an image that has a more-or-less uniform histogram, shown below.
Passing this image through the transfer function above yields the histogram below.
Note the absence of certain codes in the histogram. I call this phenomenon “histogram depopulation.” Wells calls it histogram “combing”.
Histogram depopulation cannot be corrected by subsequent conventional point processing. The following shows the histogram of the image that results from passing the test image through two complementary curves, one similar to the concave upward one above, and the other concave downwards.
If it were not for histogram depopulation, the completely populated histogram of the original image would result. Although the codes that were eliminated in the parts of the darkening transfer function that have a slope of greater than one are mapped back to their original locations by the inverse operation, the inverse operation has slope greater than one in the dark areas, causing additional codes to lack representation.
Histogram depopulation occurs whether you’re lightening or darkening images. If you’re using any curve that has a slope of greater than one in any region, histogram depopulation will occur in that region.



Leave a Reply