The effect of Q on sharpness

In the preceding few posts I explored imaging system Q, a metric for imaging system balancing. It was developed for use with monochromatic sensors and diffraction-limited optics, a luxury not enjoyed by most normal photographers. I explored the extension of the metric to cameras with Bayer color filter arrays (CFAs), with inconclusive results.

In order to gain insight as to how the concept of Q plays with Bayer CFAs, I modified a simulation that I had previously written in Matlab, adding the ability to model the diffraction of perfect lenses.

Here are the parameters I used for the simulation:

• Perfect, diffraction-limited lens set at f/8.
• 550 nm light used to calculate diffraction, even for the red and blue planes.
• Kernel used for diffraction convolution 4 times as wide and tall as the Sparrow distance.
• No vibration, no focus errors, no photon noise.
• 14 bit perfect ADCs in the camera.
• 100% fill factor.
• Camera primaries are the AdobeRGB primaries.
• Sensor dimensions are 3840 micrometers (um) x 2560 um.
• Bilinear interpolation for demosaicing.
• Q’s from 1 to 4. As Q goes up, the sensels get smaller, and there are more of them.

I fed the simulation a slanted edge image like this:

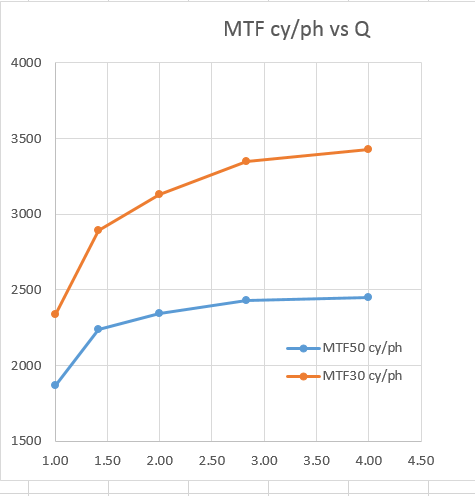
I exported the results to Imatest and had it calculate MTF50 and MTF30, the modulation transfer function values at 50% and 30% modulation. Here are those two measures of medium and lowish contrast sharpness plotted against Q:

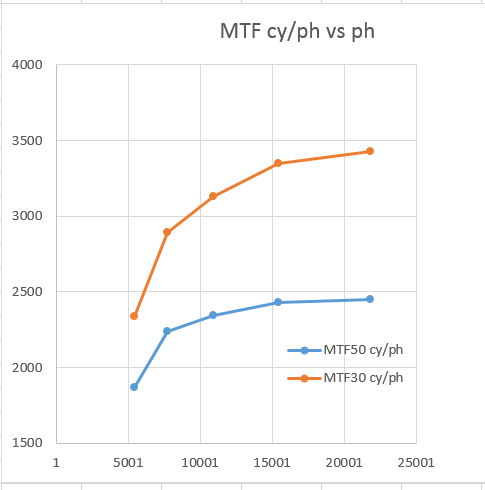
Here are the same metrics plotted against picture height in pixels for a 36x24mm (full frame) sensor:

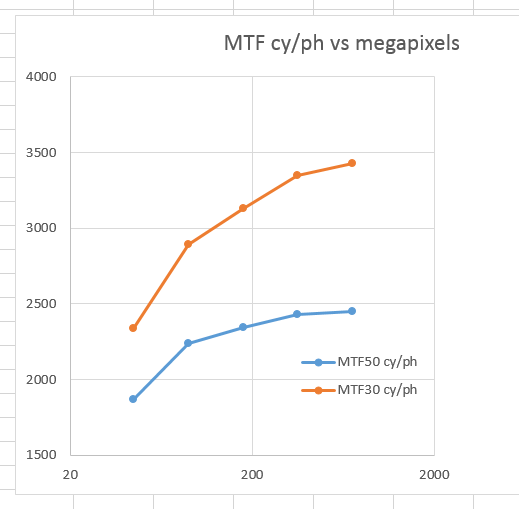
And against the number of megapixels in a 36x24mm sensor

For MTF50, by a Q of 2.8, there is no advantage in decreasing the pixel pitch for the f/8 lens. With a monochromatic sensor, that point would have occurred at Q=2. However, if we tolerate somewhat lower-contrast, there is a small advantage to be gained in going to Q=4. However, we are unlikely to see full frame cameras with a pixel pitch of 1.1 um (which is what Q=4 works out to) anytime soon.

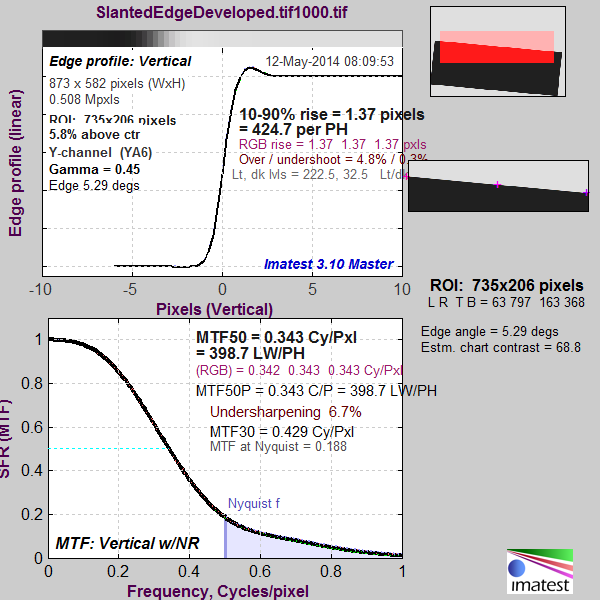
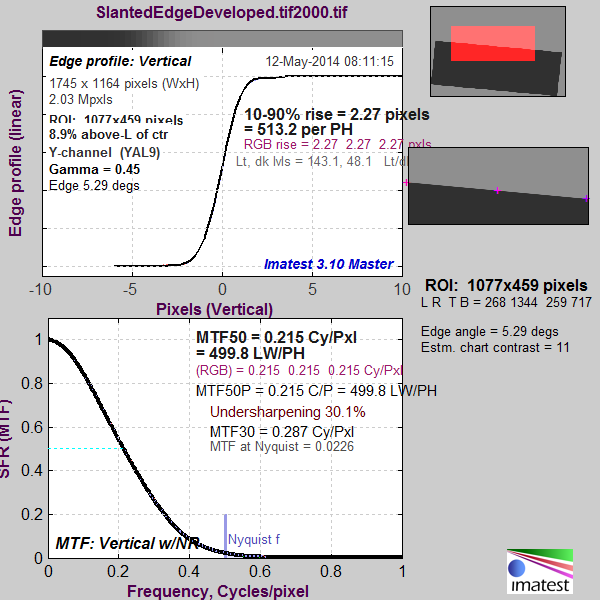
Here’s what the Imatest MTF graph looks like for a Q of 1:

There’s quite a bit of aliasing, as shown by energy above the Nyquist frequency.

For a Q of 2, the graph looks like this:

You can see how the MTF in terms of cycles/pixel is going down as the Q goes up, but there are enough more pixels to make the cycles per picture height go up. There is substantially less aliasing, but there’s still some there.

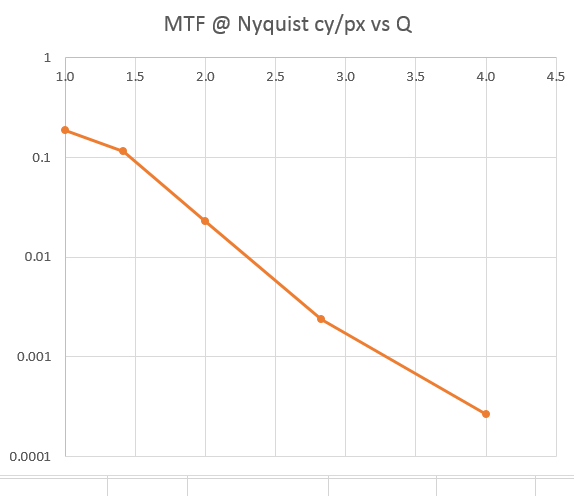
If we plot the MTF at the Nyquist frequency versus Q, which is a measure of aliasing potential, we get this: