This post is related to a test of the following macro lenses :
- Sony 90mm f/2.8 FE Macro
- Leica 100mm f/2.8 Apo Macro-Elmarit-R
- Zeiss 100mm f/2 Makro-Planar ZF
- Nikon 105mm f/2.8 Micro-Nikkor G VR
The test starts here:
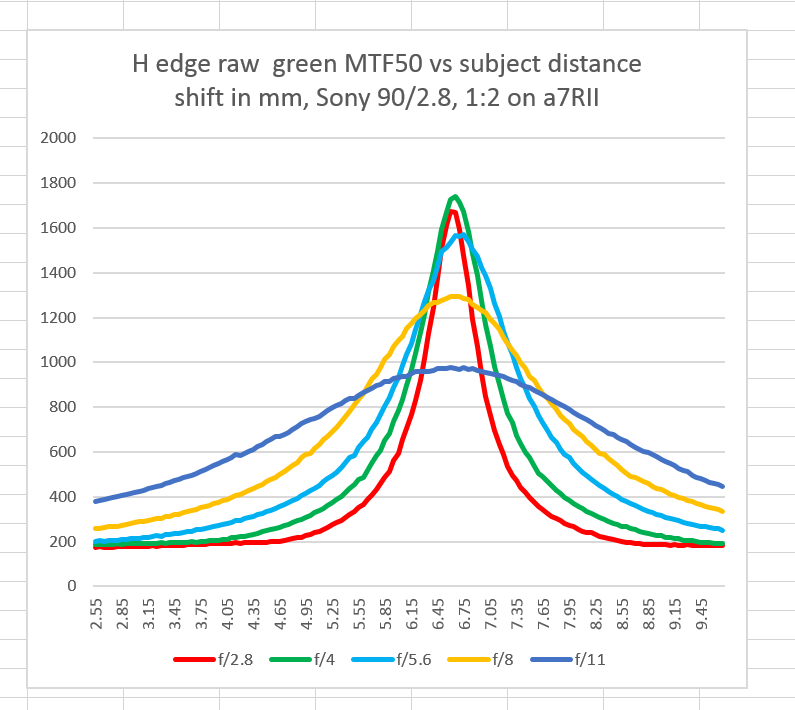
Recall the focus shift curves from earlier in this test. Here’s the one for the green raw channel of the Sony 90/2.8:
I’m going to ignore the focus shift information in this graph, which is embodied in the difference in horizontal location of the peaks, and concentrate on the vertical differences in the peaks, and how rapidly the curves fall off with distance.
Considering just the green channel, f/4 is the sharpest f-stop, with f/2.8 a very close second, and f/5.6 third. I only ran the tests at whole f-stops, so it’s possible that there is an intermediate stop that is sharper than the ones that I tested.
Others have reported that the sharpest stop for this lens is narrower than f/4, and the idea that it’s at nearly its sharpest wide open is not conventional wisdom. Why is that?
One possibility is that sharpest stop using a the luminance of demosaiced image as the image to be analyzed is indeed narrower than f/4. Another cause might be that other people have done their testing at different magnification than 1:2. I know that I’ve not seen another report on 1:2 on-axis sharpness. A third possibility, which I consider likely, is that other reviewers have missed the critical focus point at the widest apertures.
No shame there, if that’s the case. I know that my former methods, before I started doing what is in this context automatic focus bracketing with a motorized focusing rail, I never could have consistently hit the best focus distances with this lens, or any other fast, high performance lens that I’ve tested. I could get close enough to compare different lenses, but not close enough to precisely, repeatably, hit the peaks bang on.
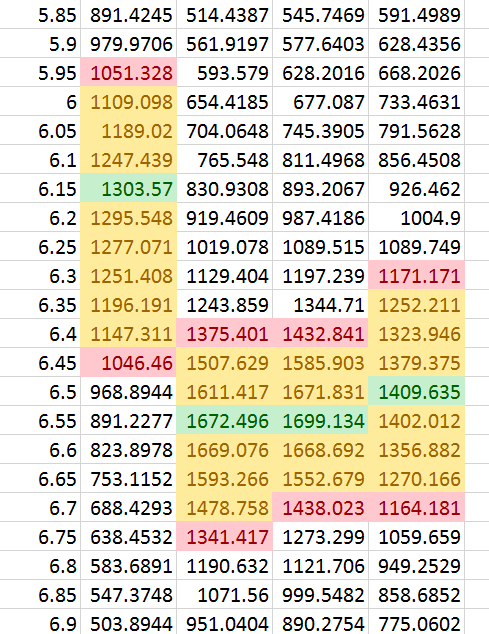
To give you an idea of how fine the distance differences are at those peaks, consider this table from the Sony 90/2.8 test with the lens at f/2.8:
Let me orient you. The left column is distance in cm. The other columns are, moving from left to right, red channel MTF50, green channel MTF50, blue channel MTF50, and luminance MTF50. All the MTF50 numbers are in cycles per picture height (cy/ph).
I shaded the peak values for each column in green. Then I identified the points in each column where the MTF50 values dropped to more than 200 cy/ph from their peaks. This is about the difference between a really good lens and a great one. I shaded the cells in between in tan.
The first thing to notice is that the red channel spread is broader than the other two raw channels. We are at a point in the aperture range where diffraction should not be playing much of a role (the Sparrow distance at 550nm covers more than four pixels), so I don’t think we can explain this as red light suffering from more diffraction. Rather I think it’s a phenomenon I’ve see often since I started doing this testing, but don’t have an explanation for: the lower the peak, the broader it tends to be. This would of course be the situation if we were limited by DOF, but I also see it across lenses. If it is a near-universal occurrence, then truly outstanding lenses need to be focused more accurately than run-of-the-mill ones.
Now, let’s look at the range of distances for which less the MTF50 is within 200 cy/ph of the peak. In the luminance column, that range spans 300 micrometers (um), or 0.3 millimeters (mm). In the green and blue channels, the range is even less: 250 um. In the red channel, we see a relatively relaxed 400 um. That shows how little margin for focusing error there is at f/2.8 and 1:2 magnification.
I never could have found and characterized those f/2.8 peaks without the motorized rail. The focusing ring is marginal, and moving the camera by hand on a rail in 50 um increments is an exercise in futility.
In my mind, that’s the most likely reason that others have reported this lens sharpest apertures are narrower then f/4. This criticism also applies to the slanted-edge lens testing that I’ve done before I started using the motorized rail.
There’s also an implication for photographers trying to get the most out of fast, high-performance lenses. You really have to nail the focus, and that isn’t easy, even with live view (I believe that it’s essentially impossible without it, unless you use autofocus in a way and for a subject that makes it reliable).
Jim said:
“the red channel spread is broader than the other two raw channels… don’t have an explanation for: the lower the peak, the broader it tends to be”
Brandon Dube said:
“If these results are along the optical axis and the lens is well centered, the drop in the MTF may be attributed purely to spherochromatism, a variation in the quantity of spherical aberration with respect to color. ”
So I would infer that in order to correct G (and B) for spherical aberrations there is a compromise elsewhere, which results in a larger minimum blur spot in the R wavelengths. Larger minimum blur spot also means a less ‘peaky’ curve off the minimum. And yes, the same reasoning goes for out of focus behavior, so better lenses need more care to make sure that peak focus is achieved.
Jack
Thanks, Jack.
Jim, is the ‘luminance’ column MTF Mapper’s measurement of the white-balanced raw data, or some combination of the individual color plane readings?
It’s MTF Mapper’s measurement of the white-balanced raw data.
I should probably use something more like what you came up with, but I didn’t expect to present that data originally.
Jim
Presumably, always dangerous, focus stacking overcomes the margin for focus plane error in a 3D object and would also if, non intuitively, used for a 2D subject given only 0.3mm to play with, though it’s going to be tough to find 2D objects that meet that standard unless it’s a razor blade of course.