This is a continuation of a report on new ways to look at depth of field. The series starts here:
A reasonable, if somewhat relaxed, portrait distance for a 55mm lens is 2 meters. I have done some actual DOF testing with the 60mm f/4 Coastal Optical macro lens as a byproduct of looking for focus shift and longitudinal chromatic aberration (LoCA).
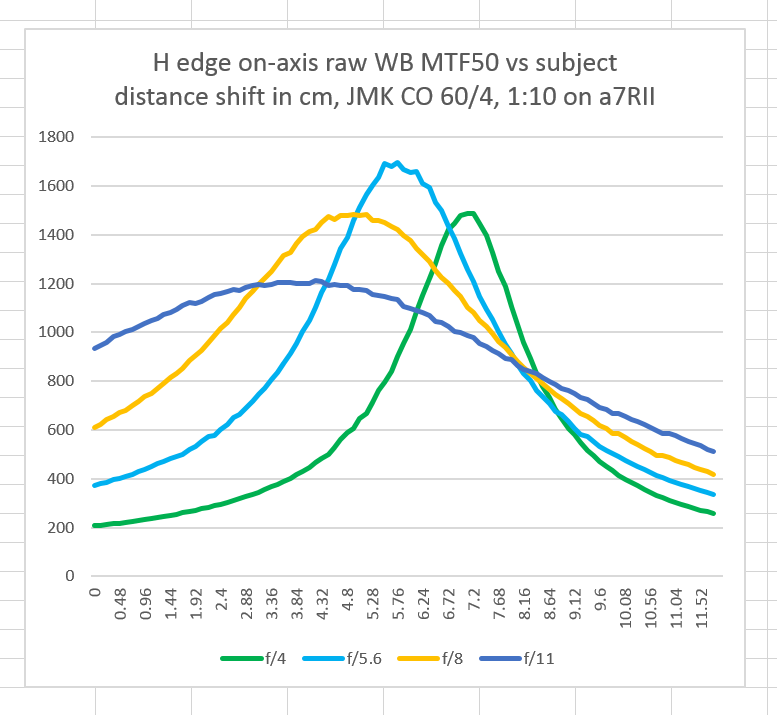
Here’s what one of those curves looked like at 1:10 magnification, which is much closer than 2 meters.
Distance is the horizontal axis, with the left hand size having the subject farther from the camera than the right hand side (The camera moves closer to the subject after each exposure). There were 101 exposures in the series, and thus the total travel was 120mm. The vertical axis is MTF50, measured in cycles per picture height, assuming the entire sensor is used.
I asked my simulator to plot a similar set of curves for a 55mm lens at 2 meters distance.
The horizontal axis of the graph is subject distance in meters. The vertical axis is MTF50 measured in cycles per picture height. The simulated sensor is 42 MP, 14 bit, full frame Bayer CFA with no AA filter, like the sensor in the Sony a7RII. Fill factor is 100%. I turned off all sources of noise (photon, read, PRNU) — they don’t affect slanted edge measurements much anyway, since the technique is intended to calibrate out noise. Diffraction is computed at 450, 550, and 650 nm for the respective blue, green, and red raw color planes. The CFA is Adobe RGB, and the illuminant is D65.
I’m using a lens blur model that I originally created a couple of years ago to approximate the on-axis behavior of the Zeiss Otus 55/1.4. Now that I have improved my focusing accuracy with a motorized rail and my target with a razor blade edge, I now realize that my Otus model is actually somewhat worse than the lens itself, particularly at wide apertures. Nevertheless, it can serve as a stand-in for very good, if not great, 55mm lenses.
You’ll notice that there isn’t any focus shift. That’s because I didn’t program any into my model for this lens. You’ll also notice how little DOF there is for critical work, even stopped down to f/5.6 or f/8, which many people — but not me — think of as having too much DOF for portraits.
This Is a good opportunity to think about whether the end of acceptable DOF a function of the maximum resolution at that aperture, or is it absolute in some sense? I welcome anyone’s point of view on that subject. This is not a tradeoff usually associated with DOF calculations.

The relationship between acceptable DOF and maximum mtf depends, I think, on the use case. For portraiture it’s nice to have an incredibly sharp eye and the rest of the face sharp enough slits not a mass of blur, but noticeably less sharp than the eye (at least for headshots or similar). But some other kinds of images benefit from a more uniform look within the DOF
Is apparrent DOF tied more to peak resolution or the slope of resolution falloff? Slope looks similar f2 thru f5.6 with higher peaks and wider envelope at any given resolution, but as you go to f16 slope flattens and resolution is more consistent. Easy to see f4/f8 have similar max resolution with f8 slope sustaining that resolution over greater DOF. Same for 2.8/11 and 2/16 – clear case of stopping down giving deeper DOF. But how do you compare f5.6 to f16 – both exceed 1000 for 20cm (depth of a head roughly) and if foreground is empty and background many meters distant so only that 20cm matters, is the consistent resolution of f16 or the high peak and steep slope of f5.6 going to appear in ‘better focus’ across the key 20cm? Does f5.6 have better apparrent DOF than f16 for purpose of a portrait? Would different enlargement effect which appeared in better focus?
Separately, how might the steep slopes impact ability to use focus stacking to achieve both high and consistent resolution over 50cm, or a few meters, or for a landscape with foreground elements. Do I face a form of zeno’s paradox as I focus closer and closer….