This is a continuation of a report on new ways to look at depth of field. The series starts here:
On DPR, someone asked an excellent question:
We frequently talk about focusing at infinity, or at some large distance, but it often seems, to me at least, that there is hardly a difference between focusing at 3000 feet and 5000 feet with some focal lengths.
So what focusing distance in your lens model is effectively infinity? What is the focus distance X where the MTF50 value at infinity is 90% of the maximum at a given f/stop? How can we generalize this to other lenses?
I thought I’d take a crack at it. Unfortunately, my simulator is way too slow for casual explorations of this kind of thing. Just in time, Jack Hogan has written a Matlab program to approximate the spatial frequency response (SFR) results of my simulation. Jack’s program delivers results in seconds instead of hours.
Jack spec’d a test lens that approximates the results that I’m getting from my simulator at f/5.6 and narrower apertures, but is closer to diffraction limiter at wider ones. I’m going to use that lens for today’s testing. In the fullness of time, I’ll work on more sophisticated lens models, but we don’t need them to learn something useful about the question above.
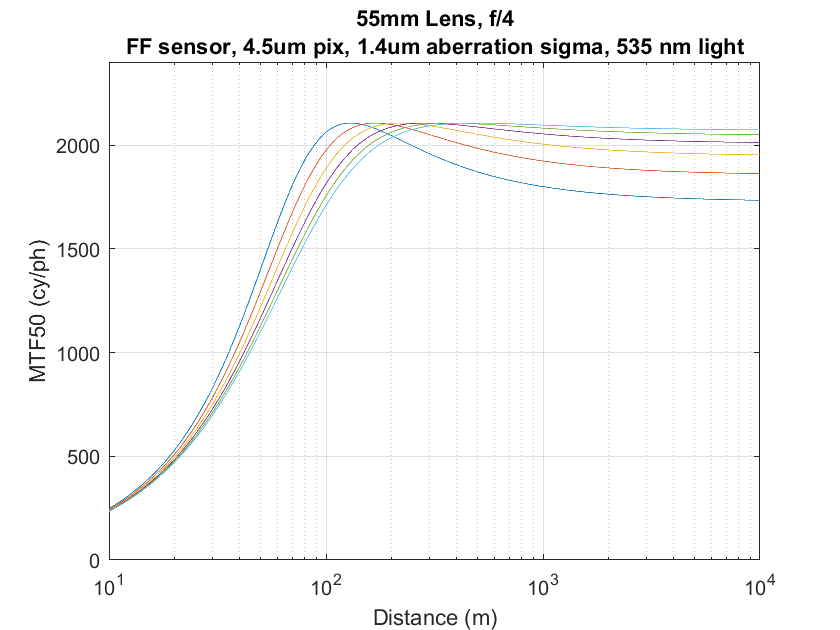
I set up the program to plot a set of curves of MTF50 versus subject distance for various focused distances with the aperture set to f/4 on a 55mm lens:
The above is for a Sony a7RII. The sensor affects the results to some extent, but, over the range of modern full frame sensors, not strongly.
As you can see, the closer you focus, the peakier the curve is, and the worse the MTF50 at infinity — in this case, I’m going to let 10 km, or about 6 miles, stand in for infinity. At that distance, if you’re a typical recreational runner, it would take you about 45 minutes to run from your camera to your subject. The drop from the peak MTF50 (which doesn’t change with focusing distance) at 10 km if what we want to look at.
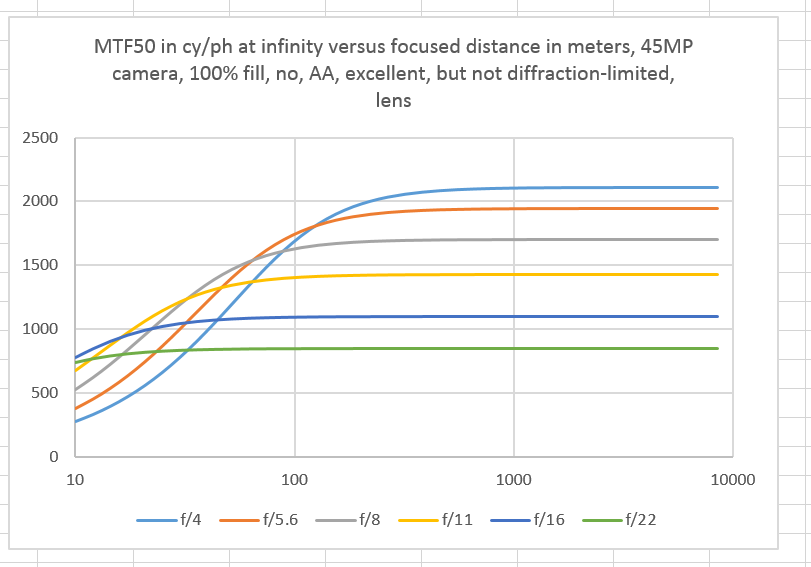
Let’s plot MTF50 at infinity versus focusing distance for the whole f-stops between f/4 and f/22.
Let me empathize the difference in the x axis between the plot immediately above and the first one. In the above plot, the horizontal axis is focused distance. In the first plot, that axis is subject (or object, if you prefer) distance.
You can see that the dropoff in values occurs more slowly as we stop down. That’s what depth of field is all about. But because of diffraction lowering the infinity-focus, infinity-measured MTF50, it’s hard to get a handle on the question we’re trying to answer.
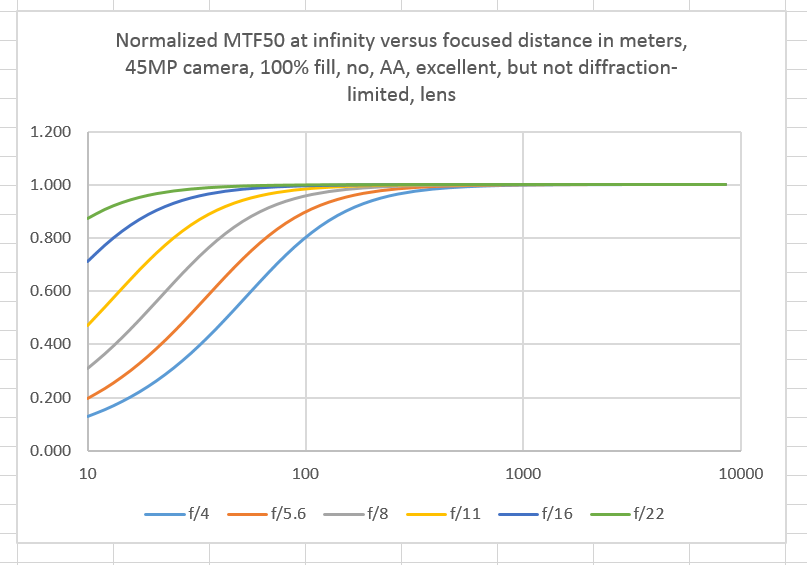
We can normalize each of the curves to the MTF50 value that we get when the lens is focused at infinity:
That’s more like it.
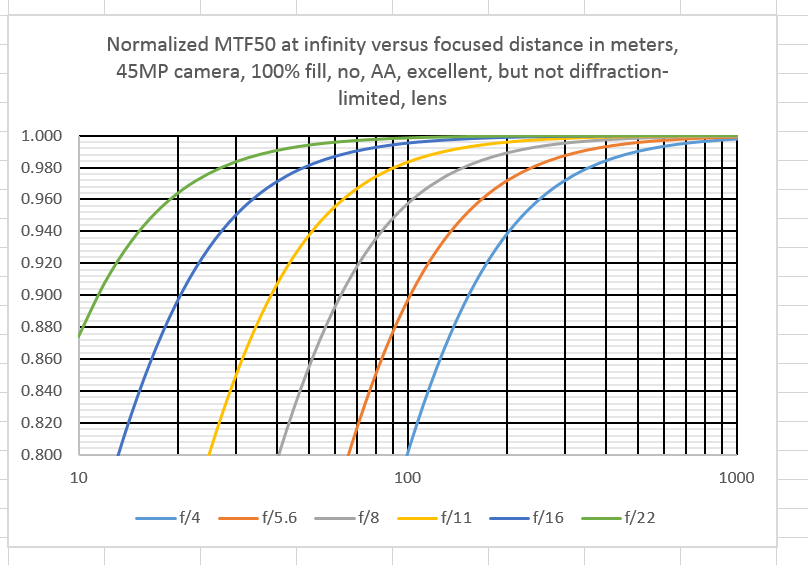
Now let’s zoom in, and add some grid lines so that we can read off the distances we’re looking for:
90% is right in the middle of the vertical axis. You can read off the focusing distances where the MTF50 is 90% of that when the lens is focused at infinity.
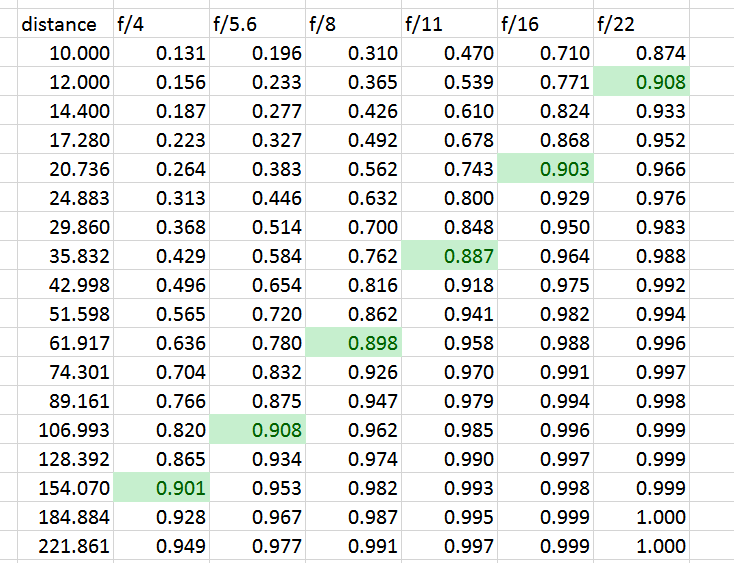
If you’d like to see it in tabular form, here it is:
The 90% distances are marked in green.
How would we generalize this to other focal lengths? We’d normalize the distances by multiplying by the focal length squared. [Thanks to Jerry Fusselman for catching my previous normalization error.]
So, for the f/4 case, the constant to be multiplied by the focal length squared is 50900. To get the distance for a 55mm lens, we multiply the constant by (0.055)^2, and get 154 meters. To get the distance for a 200mm lens, we multiply 50900 by 0.04, and get 2040 meters. For a 500mm lens, the distance is a whopping 12000 meters! In the case of an 18mm lens, the distance is a paltry 16.5 meters.
Here are the constants derived from the above table:
- f/4: 50900
- f/5.6: 35400
- f/8: 25500
- f/11: 8500
- f/16: 6800
- f/22: 4000
Cutting to the chase:
Is your investigation leading to agreement or disagreement with the approach advocated several week ago on a DPR thread?
http://www.dpreview.com/forums/post/57800235
IIRC, Jerry Fusselman advocated at length a PDF from the 1990’s with view cameras which has the summary of:
Focus at infinity and divide the FL by 2x to 5x
That seemed completely bogus to me, but what do I know?
My speculation is that the thought you put into that thread got you thinking about an alternative way of thinking about DOF … applicable to ultra-high digital sensors with ultra quality prime lenses.
I was initially, and remain, deeply skeptical of the object field approach. However, I try to be open-minded, and find that I often learn something when I explore ideas that seem strange to me. I started this exploration of DOF to work through my thoughts, and to explore some paths that, to be frank, I probably never would have thought of had I not read the object-field material.
So, be patient. I will eventually get around to the object field stuff.
Jim