Maximizing DOF in the face of diffraction

This is a continuation of a report on new ways to look at depth of field. The series starts here:

A new way to look at depth of field

We’ve seen in this series that stopping down giveth depth of field (DOF), and taketh away sharpness (measured in terms of MTF50,

Is there a way to get a handle on this?

Maybe.

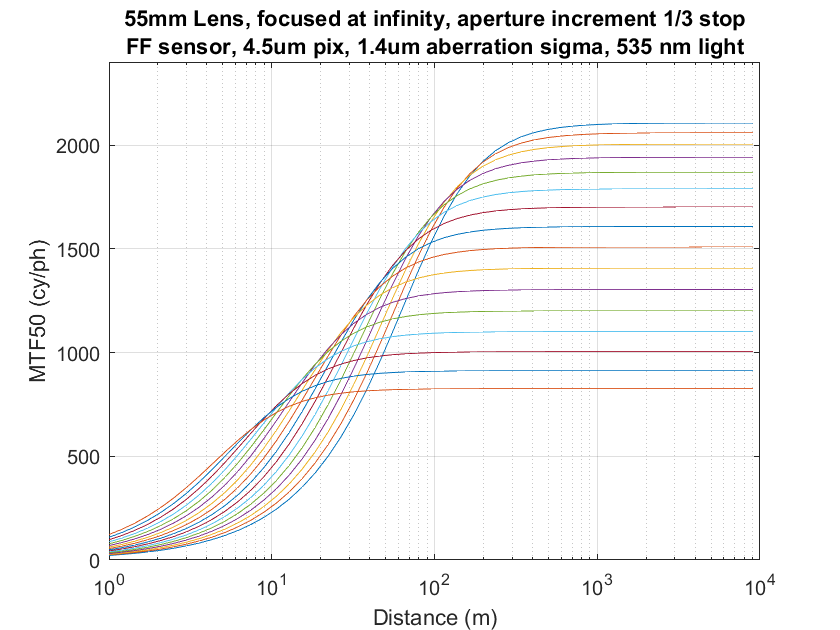
I took Jack Hogan’s MTF50 calculation program, which over the last two days has been modified into near unrecognizability, I set it to model the 55mm, not-quite diffraction limited lens that we’ve seen in the last two posts, set the focused distance to infinity (well, 10 km), the camera to the Sony a7RII, and look at MTF50 in cycles per picture height (cy/ph) vs subject distance for apertures in one-third stop intervals from f/4 through f/22.

Here’s what I got:

If you look at the cet of curves carefully, you’ll notice two thing that — at least to me — are interesting and potentially useful.

• The best depth of field for a given sharpness is obtained at an aperture that gives infinity sharpness of slightly higher than the desired sharpness.
• However, that aperture gives poorer sharpness at nearer subject distances than could be obtained by stopping down more.

How is this useful? If you’re focusing at infinity, and you have a specific object in the foreground that you want to be sharp, pick an f-stop is near the widest one that delivers the desired sharpness. Anything closer than your chosen object will suffer from this decision.

Conversely, if you’re focusing at infinity, and have a foreground so deep that you know you won’t be able to get it as sharp as you want, decide how much sharpness you really need at infinity, and stop the lens down to that aperture.

The first approach is entirely compatible with the hyper-hyperfocal distance approach discussed in the preceding post, if you focus on the HHFD instead of infinity.