This is a continuation of a report on new ways to look at depth of field. The series starts here:
Yesterday, we looked at the focus distance that made a minimal impact on the sharpness for objects at infinity, with minimal being defined as a reduction of MTF50 by 10% from the value when the lens is focused at infinity at the same aperture.
Those of you skilled in the art of conventional DOF calculations will recognize the above method as conceptually similar to the derivation of the hyperfocal distance. However, the numbers that I came up with in yesterday’s post are quite different than the ones that you’d find in the DOF card that came with your Leica M3 or Nikon F, and similarly different from what you’d get setting the hyperfocal distance using the DOF ticks on your lens barrel, which assume a circle of confusion (CoC) of about 30 micrometers (um).
That isn’t to say that MTF is MTF and CoC is CoC and never the twain shall meet. MTF50 and CoC are correlated, and with some simplifying assumptions, for any sensor there is a mapping from one to the other. You could get results similar to what I got yesterday by judiciously picking the CoC for each aperture; it would be exceedingly small by conventional DOF standards.
So what do we call the distances that I came up with yesterday. My proposal is the hyper-hyperfocal distances. The “hyperfocal” is a nod to the concept from the conventional DOF canon; the additional prefixing “hyper” is a reference to taking the concept farther than it’s gone before, and maybe a comment on the mentality of those who might use the freshly-minted concept in the future. For concision, I’ll abbreviate the term to HHFD.
I went back and reworked yesterday’s calculations extending the far object distances to increase accuracy. [Thanks to Jerry Fusselman for catching a normalization error that I’ve now fixed.] I’ll put the focal length in mm, and the distance in meters.:
- f/4 — 0.0595 * (focal length)^2
- f/5.6 — 0.0397 * (focal length)^2
- f/8 — 0.0264 * (focal length)^2
- f/11 — 0.0149 * (focal length)^2
- f/16 — 0.0083 * (focal length)^2
- f/22 — 0.0046 * (focal length)^2
For the 55 mm lens that I’ve been using, rounded numbers are:
- f/4 — 180 meters
- f/5.6 — 120 meters
- f/8 — 80 meters
- f/11 — 45 meters
- f/16 — 25 meters
- f/22 — 14 meters
Remember, these are for the Sony a7RII. There is currently no full frame camera with significantly higher resolution. If you have a camera of significantly lower resolution and/or and antialiasing (AA) filter, like an a7S or a7SII, the distances will be somewhat lower. When that great day dawns and we have 200 MP full frame cameras, the HHFDs will — gulp — be even longer.
Eyeballing those numbers, you might see a practical problem: how are you going to set those distances accurately on any lens but a manual focus tele? Well, that’s a problem. Let’s put it aside for now; I can think of at least one workaround.
Would setting lens to the HHFD instead of just saying the heck with it and setting it to infinity provide any useful foreground sharpness in a landscape where most of the subject was at infinity?
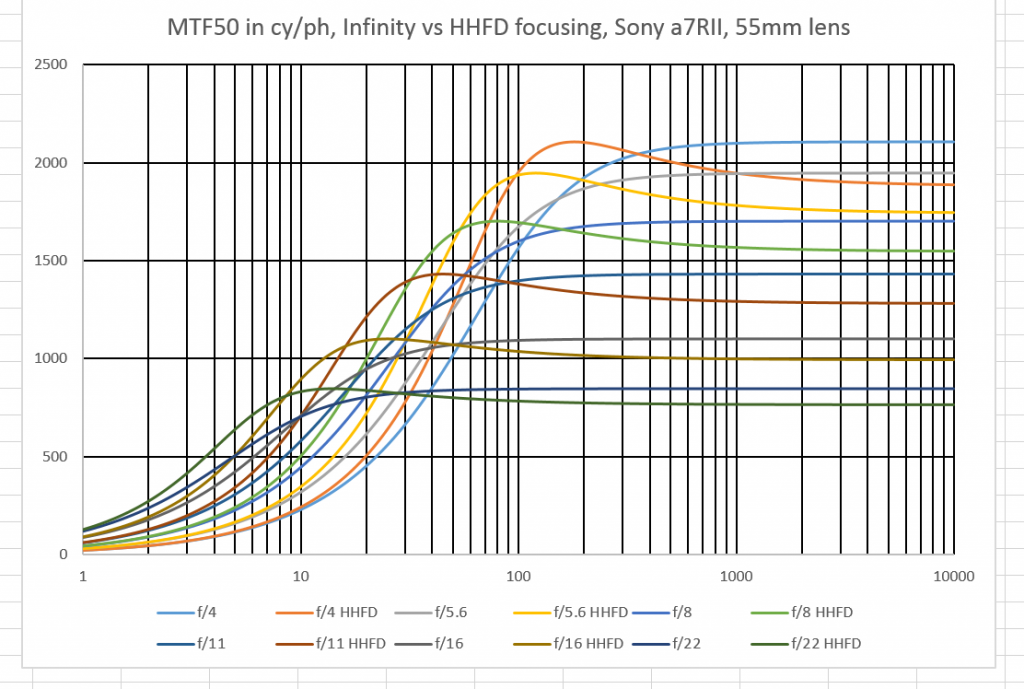
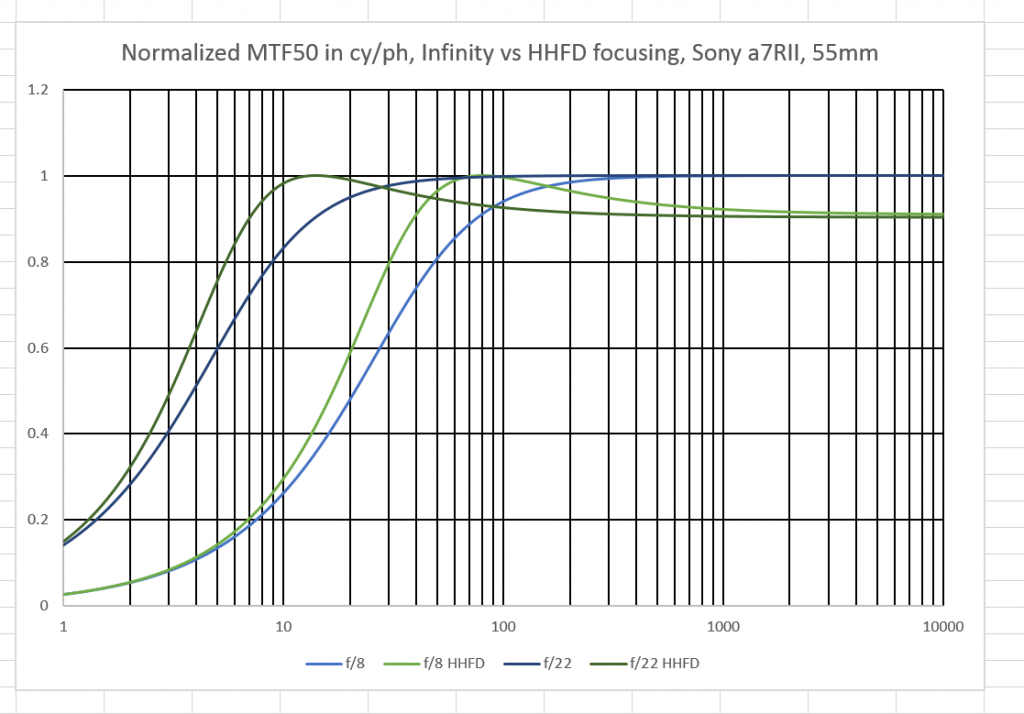
Let’s find out. Here are all the whole f-stops from f/4 through f/22, with a 55 mm lens focused at infinity and the HHFD:
If that’s confusing, don’t worry; I’m going to simplify things.
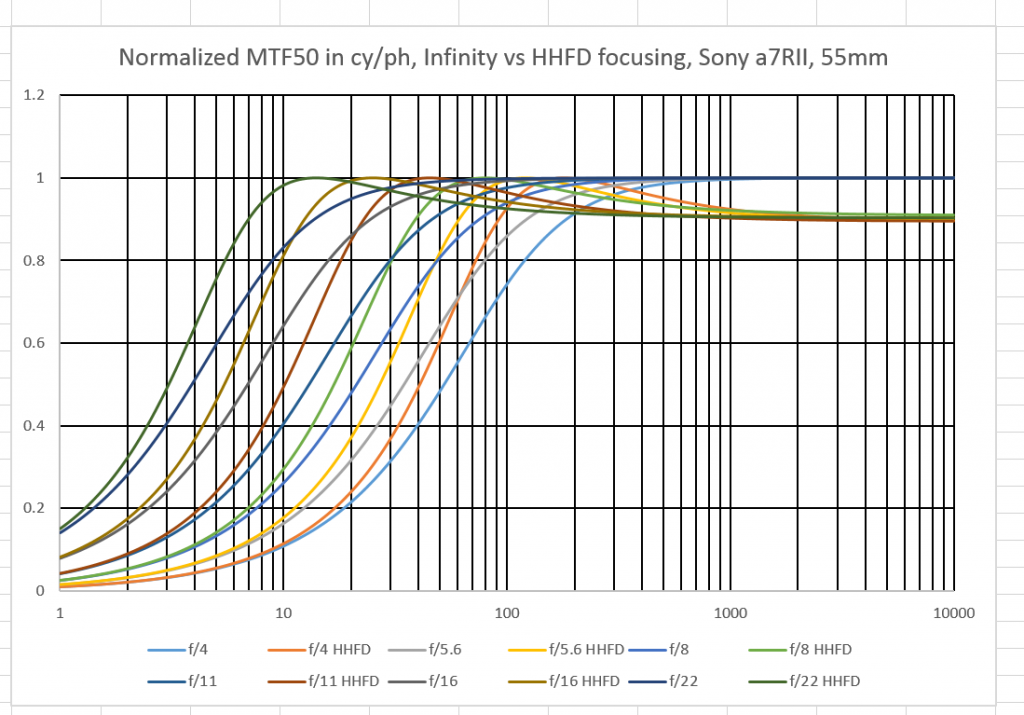
But before I do, Let’s look at the curves normalized to the infinity-focused MTF50 for each f-stop:
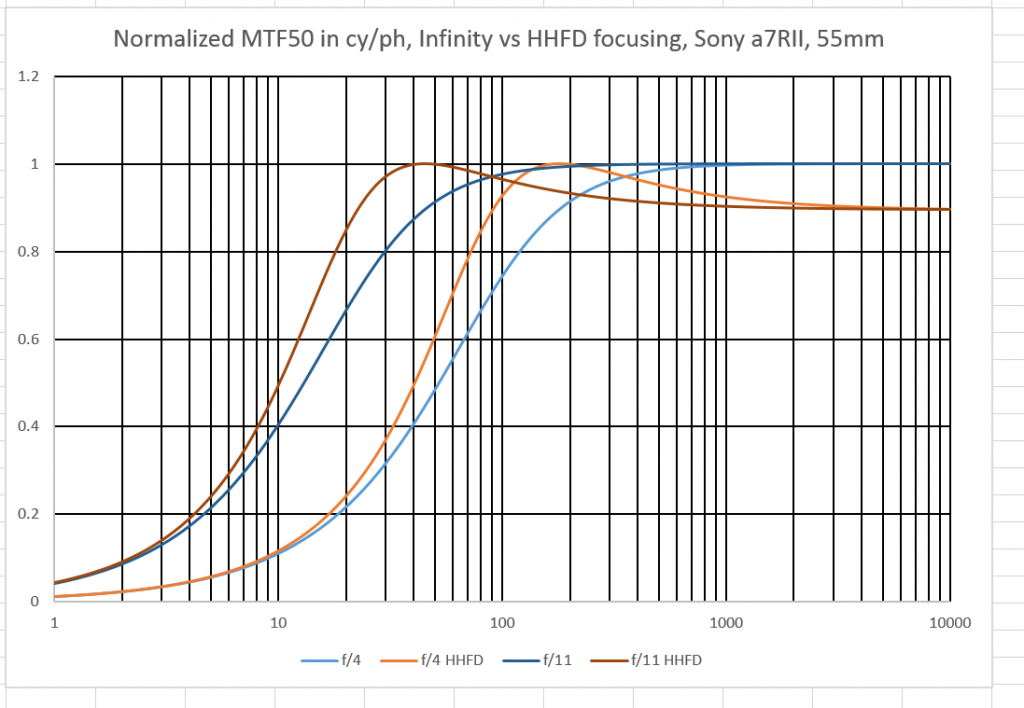
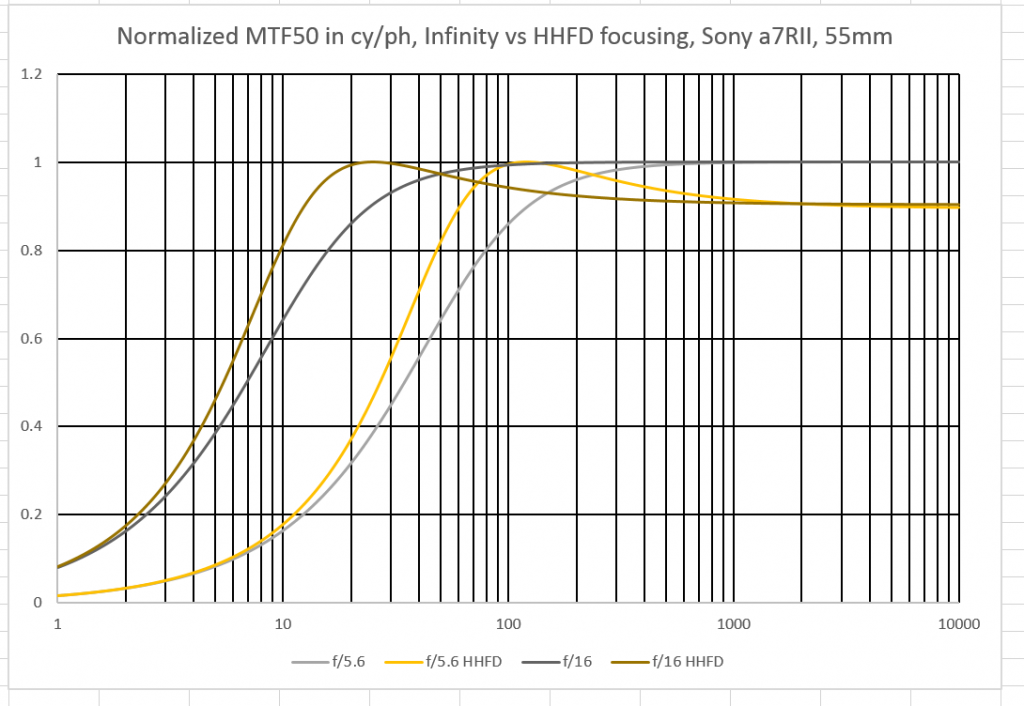
That’s rather pretty, at least to me, but it’s too complicated to work with. I’ll show you some subsets with only two f-stops per graph.
If we use the 0.9 line (almost 2000 cy/ph) as our cutoff for the f/4 curves (this is probably unrealistic, as that number is shockingly sharp and unlikely to be actually obtained with the usual field atmospheric conditions), the HHFD setting has given us highly acceptable sharpness at 100 meters instead of at 200 meters for infinity focusing.
Looking at the f/11 curves, we see that the infinity-focused lens resolution at 50 meters is about the same as the HHFD-focused lens at less than 25 meters.
At the f/5.6 curves, we see that the infinity-focused lens resolution at 140 meters is about the same as the HHFD-focused lens at 60 meters. For f/16, the near limit of this high standard of acceptability goes from 25 to 15 meters.
At f/8 and f/22, the pattern of the HHFD having acceptable sharpness at half the near cutoff distance for infinity focusing continues.
I can think of situations in which knowing the HHFD would be useful.
Does the near side of the threshold of sharpness chosen for that particular HHFD still remain at 50% of the set distance for other normalized MTF50 thresholds other than 90%?
If I understand your question right, the answer is no. The distance differences between the infinity-focused and HHFD shots grows smaller as the bar is lowered. If the HHFD were adjusted to the new bar, then I don’t know what would happen.
You may be familiar with this article from Keith Cooper on hyperfocal distance:
http://www.northlight-images.co.uk/article_pages/hyperfocal_distance.html
It significantly influenced how I deal with DOF, and became underwhelmed with DOF calculators.
>> Eyeballing those numbers, you might see a practical problem: how are you going to set those distances accurately on any lens but a manual focus tele? Well, that’s a problem. Let’s put it aside for now; I can think of at least one workaround.
How about the distance scales for Sony lenses. My FE55 has 512m. However, I don’t know how valid / repeatable / accurate it is. I’ve tried to get numbers for the Batis 85 from B85 owners, without success.
Nit: some of your sentences are getting pretty complicated:
>> If we use the 0.9 line (almost 2000 cy/ph) as our cutoff for the f/4 curves (this is probably unrealistic, as that number is shockingly sharp and unlikely to be actually obtained with the usual field atmospheric conditions), the HHFD setting has given us highly acceptable sharpness at 100 meters instead of at 200 meters for infinity focusing.
I can understand that you, probably being more of the Ernest Hemingway than the William Faulkner persuasion, might feel uncomfortable with sentences whose diagramming (I remember spending a lot of seventh grade diagramming sentences; my classmates and I used to construct mind-bogglingly tricky ones in attempts to stump each other) furrows your brow, but, while I don’t plan to make it a routine practice, I think that there is a place in the blogosphere for sentences that, while not as long as some of Faulkner’s best, don’t conform to the short-attention-span staccato pace — which I find exhilarating, but distinctly tiring at times — and so I may, from time to time, construct sentences that may, should you decide to react to them, be sufficiently offensive that you again take keyboard in hand to voice your quite understandable, and welcome in terms of offering distraction from the cares of the day, reaction to the length and complexity (is it that that sentence was too long, or too hard to follow?) of my writings.
Yes and no. 😉
BTW: The 19 verses of Ephesians 1:3-21 are two sentences with 407 words (KJV).
One of my favorite Bible translations is the NIrV. It is for readers at the 6th to 7th grade level. It splits the above into 57 sentences.
I would admit to being prone to verbosity and long sentences.
Jim
I’ve only just come across your blog and have enjoyed spending Easter reading the backlog.
I’m trying to get my head around the hyper-hyper ‘stuff’, but am simply confused by the table in this post, which doesn’t seem to correlate with a similar table in the previous post.
The one above seems to have a strangeness at f/16 and f/22. To me, not having seen the maths, it looks like you are missing a zero.
I’m keen to explore your ideas further and possibly use them in an in-camera script.
Cheers
Garry
Photography.grayheron.net
You are correct. The values for f/16 and f/22 were both missing a leading zero. They’re fixed now.
Thanks.
Jim
As you say, the HHFDs relate to a particular (Sony) camera. Not having seen the math behind the results, I wonder if it is possible, or even worth, generalizing your ideas and creating a lower bound, assuming the Sony is an upper bound.
I personally shoot with a 5D3 and, of course, Magic Lantern. This gives me Lua script access to focus etc. I helped put in the difraction corrected DoF equations, but am always looking to try other things, like your HHFD ideas.
BTW I looked at Merklinger’s ideas a few years ago, but was drawn back to the ‘classical’ CoC approach when I wrote my auto focus bracketing scripts.
I wonder if your findings are algorithmically accessible, i.e. so I can script them.
Cheers
Garry
Do you speak Matlab?
Jim
No sorry: but it was worth asking 🙂
You hint at other cameras moving the HHFD to shorter distances, but have you looked at by how much? Is it significant?
Also as your Sony HHFD is shorter than the ‘camera infinity’, it must be a better approach than focusing at infinity and setting the aperture for the near field. That is your Sony HHFD on any camera will give a ‘better’ result than Merklinger’s approach.
Or maybe I’m wrong.
Cheers
Garry
Jim
This is a very interesting series and I would like to try it out. My camera system (Fuji) has a digital scale in the EVF that only goes out to 10 meters. What is your workaround for the really long HHFD focus distances?
Thanks!
Carry a laser rangefinder. Find something at the right distance, as measured by the rangefinder. Focus on it with your camera.
Thanks, that’s a great solution! I will definately try this technique out. And thanks for doing all the research and writeup I’ve read Merklinger before and was always a bit skeptical of the results from normal hyperfocal.