Object field DOF methods and MTF50

This is a continuation of a report on new ways to look at depth of field. The series starts here:

A new way to look at depth of field

A few days ago, I gave a brief introduction to object field techniques for controlling DOF, then went on to other image plane oriented things. In this post, I’m going to circle back to the object field. If you haven’t yet read it, I recommend that you take a look at this short explanation.

This approach has its adherents and its detractors. When I first encountered it a couple of weeks ago (Thanks to Jerry Fusselman), I found it counterintuitive in places, but I now think that it has merit for some people in some situations, and I don’t find an inherent conflict between object field and image plane approaches; I think they are two ways of looking at the same thing.

I think an analogy with exposure is apt. There are many ways to get to an exposure setting. Some are wrong, but there’s not just one that’s right. Some people argue passionately for the way that works for them, thinking that it should work for everybody. But one size doesn’t fill all photographers, and one size doesn’t fit all situations. So it behooves photographers to have many ways for dealing with exposure, be open to learning new ones, and not be too quick to call the ones that they don’t use garbage. Replace exposure with DOF, and it’s pretty much the same thing.

That doesn’t mean that we have to uncritically accept every claim about exposure, and it doesn’t mean that we have to do that with DOF.

There was a claim about object field methods that I touched on a few days ago that I’d like to get into to here. Here’s how Merkingler put it:

When a lens is focused at infinity, the disk-of-confusion will be of constant diameter, regardless of the distance to the object.

The disk of confusion is what Merklinger calls the projection into the object field of the image-plane circle of confusion (CoC). The implication is that, with the lens focused at infinity, resolution in the object field is constant regardless of depth. That would be true for a lens with no diffraction (which, to be fair, Merklinger talks about), no aberrations, on a camera with no Bayer CFA and sensors that only are sensitive at an infinitesimal point in the middle of each pixel. But in real life, the situation referred to above only applies to a range of distances.

How large a range of distances?

Let’s take a look.

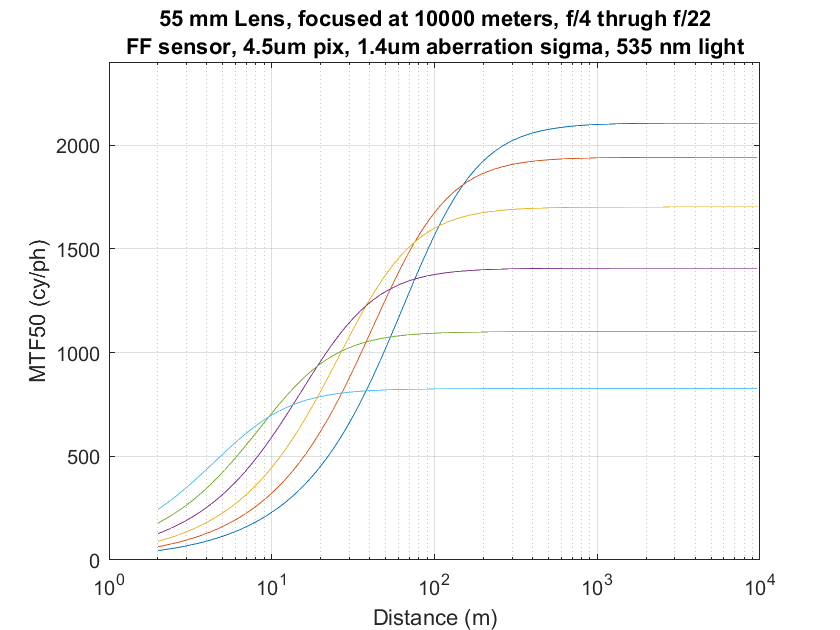
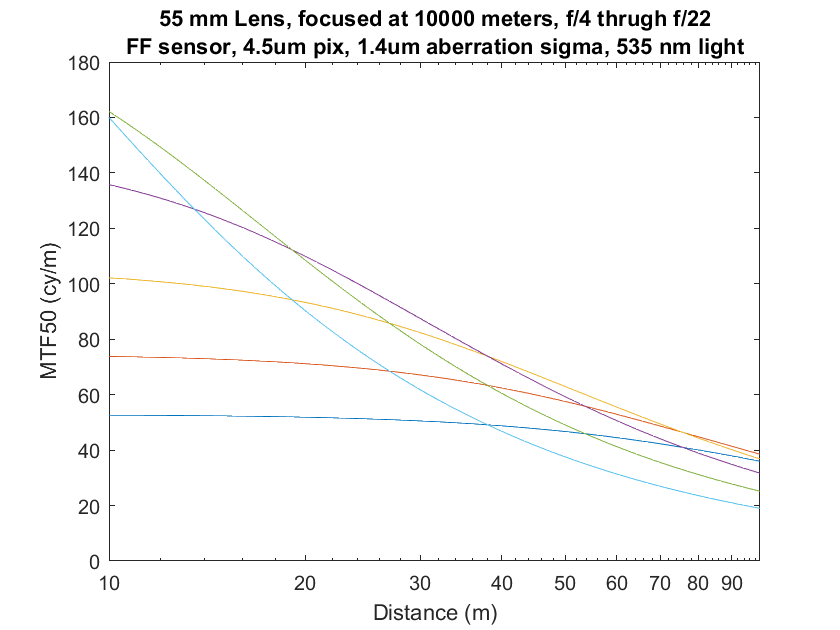
With our simulated top quality 55 mm lens focused to infinity and mounted on a simulated Sony a7RII, we get image plane MTF50s versus object distance curves like these:

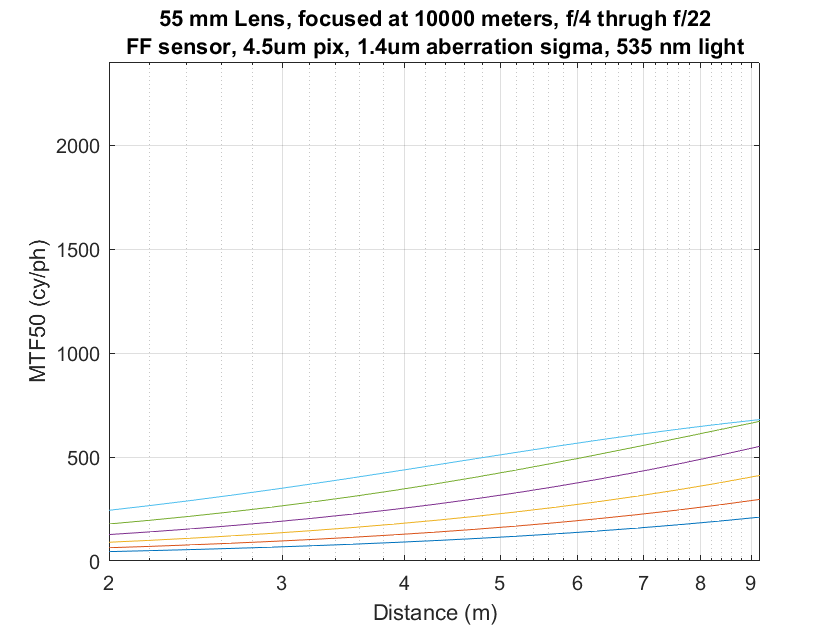
Let’s blow this up to the distances between 1 and 10 meters:

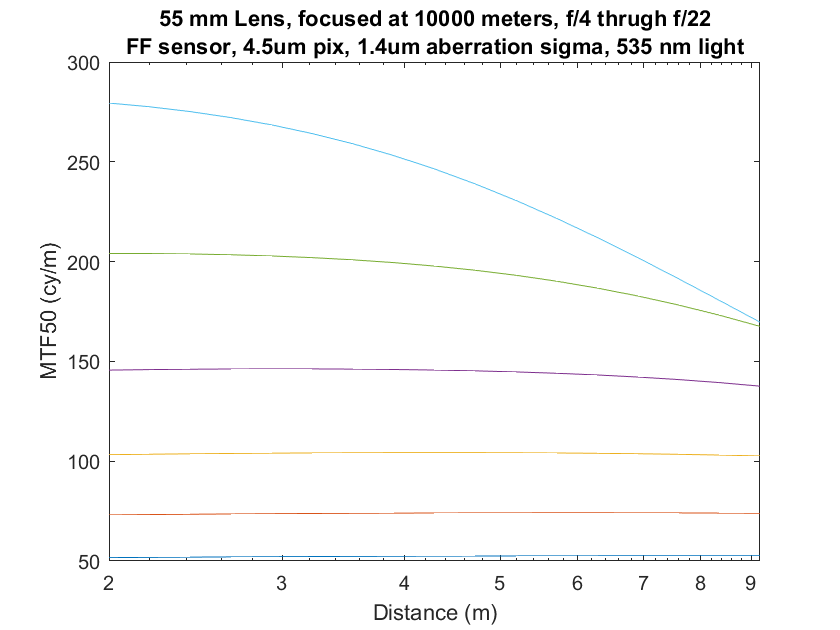
Now let’s look at that in the object field:

You can see that, although the curves for the narrower f-stops are flat as predicted, the one for f/4 is falling rapidly by the time we get to the right side of the graph. And look at the image plane MTF50s we’re getting there: only a little over 500 cy/ph for f/4. The relationship is breaking down well before the image plane resolution approaches what most of us would call sharp.

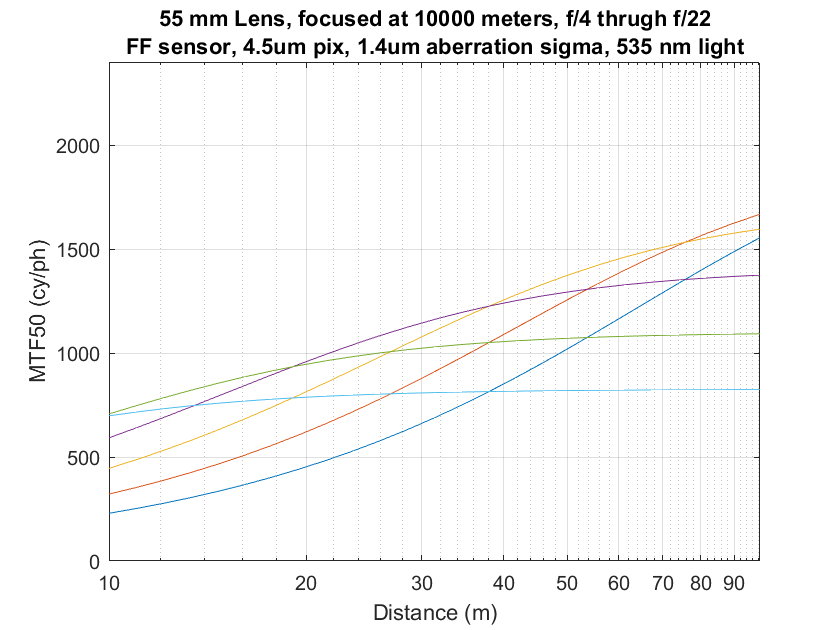
If we look at the object distances between 10 and 100 meters, first in the image plane:

You can see that it is in this region where we begin to get photographic sharpness.

Now in the object plane:

Only f/22 and f/16 are remotely flat.

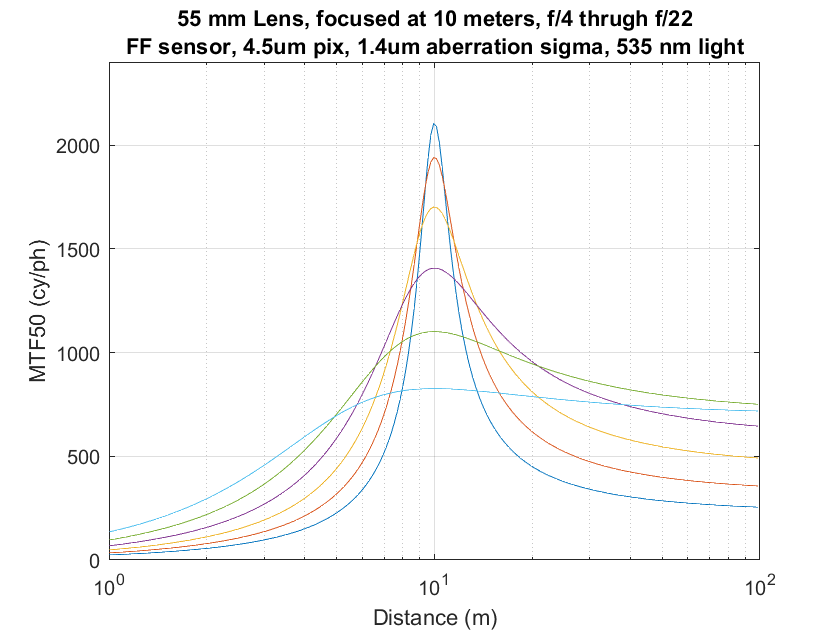
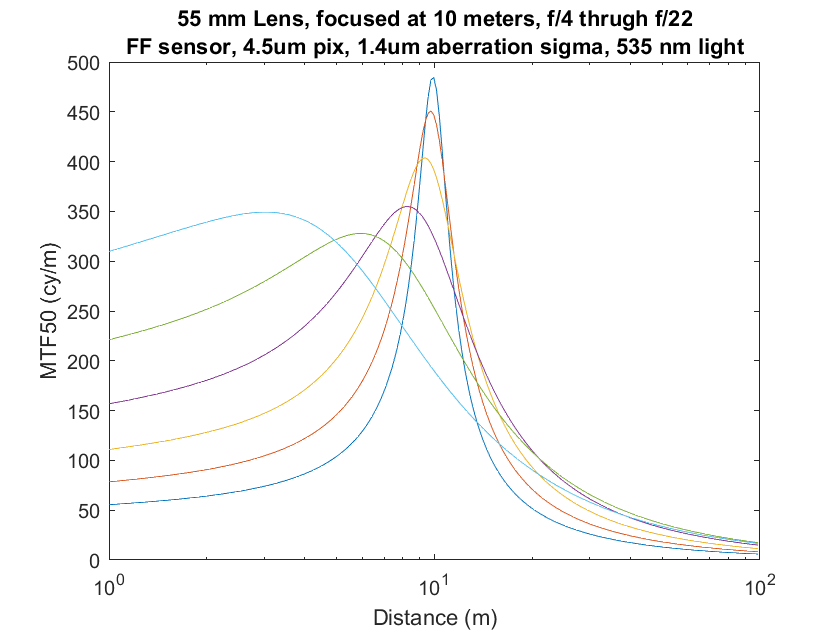
Now let’s look at image plane and object field curves when we focus the lens to 10 meters.

Image plane first:

And now the object field:

You can see that the object field resolution is biased towards the distances nearer to what was focused on, to the point where the f/16 and f/22 curves peak substantially nearer than the focus point. I had to think about that before it made sense.

After two weeks of thinking about object field methods, I still can’t figure out a the best way to use the above set of curves in my photography. I’m still working on it, though. One thing that’s clear: im object-field terms, the defocusing/blurring behavior of a lens is much more complicated than in the image plane. Consider the huge nearside-of-focus-distance sharpness variations from f/22 to f/11, ofr example.