[Note. The bilinear and bicubic interpolation algorithms referred to in this article are the Matlab implementations. They are different from the Photoshop algorithms of the same or similar names. The Photoshop versions are reported on a few posts further on. Therefore, this post is primarily of academic interest.]
In yesterday’s post I reported on the effects on photon noise when downsampling monochromatic images in a linear space. However, in Photoshop (Ps) at least, we hardly even downsample in a linear space. sRGB and Adobe RGB have gammas of 2.2, and ProPhoto RGB has a gamma of 1.8.
Changing the gamma to 2.2 has almost no effect on the rms noise. That’s nice.
However, changing gamma to 2.2 does affect the histogram of the noise. I set out to measure that.
In statistics there are two central moments immediately beyond the variance, the square root of which is the standard deviation. They are called skewness and kurtosis. Skewness measures asymmetry in the histogram, and kurtosis measures peakiness.
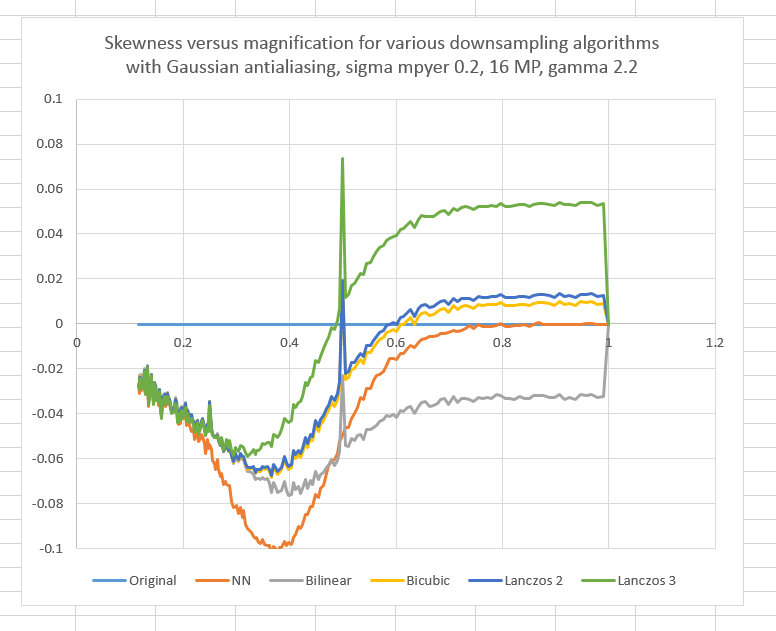
Here’s the skewness we get when downsampling images using a pre-scaling Gaussian AA filter:
It’s clear that all the resampling algorithms, including nearest neighbor, tilt the histogram. It looks like the effect begins to go away by the time the magnification is below 1/8. It’s also clear the magnification of 1/2 is special.
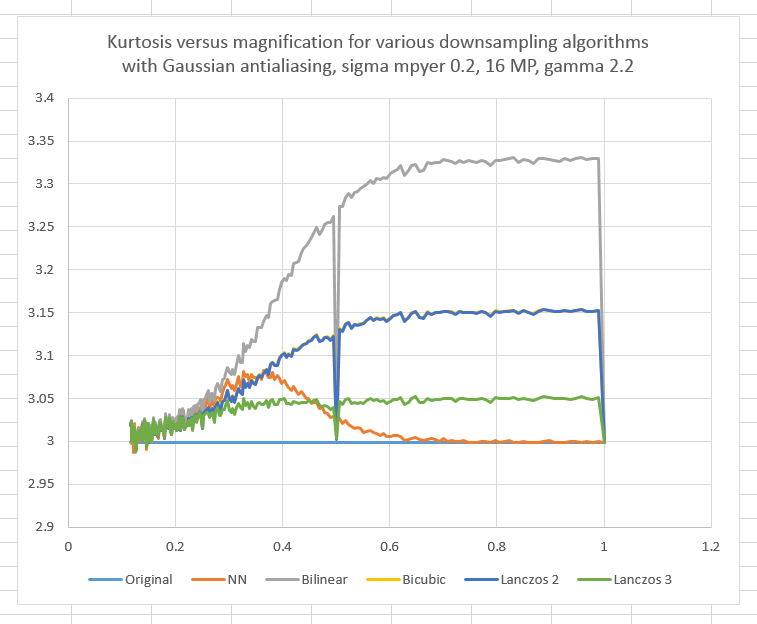
When we look at kurtosis, we see this:
Three is the kurtosis of a Normal distribution. All the resampling algorithms have to a greater or lessor extent, the ability to make the output histogram peakier than that of a Gaussian. Magnificatio of 1/2 is again, special.
Do these things affect the way that noise is perceived? I frankly don’t know, at this point.
Leave a Reply