Photoshop Gaussian noise spectrum

In the two previous posts, I identified some anomalies with Matlab’s implementation of bilinear interpolation downsampling at reduction ratios that are integral powers of two. I also observed smaller, but similar, anomalies with bicubic, Lanczos 2, and Lanczos 3 downsampling.

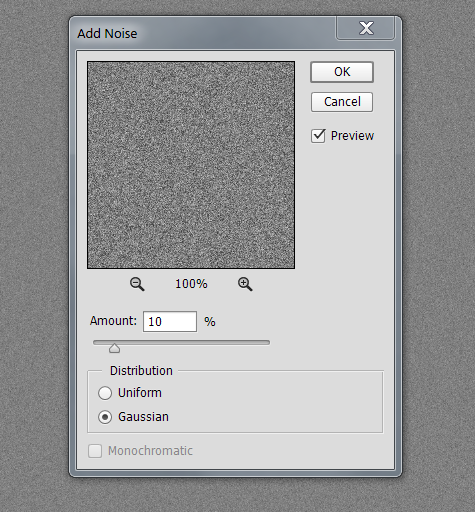
Today I set out to find out if the Photoshop implementations of bilinear interpolation evinced the same effects. I created a new 4000×4000 16-bit gray gamma 2.2 image, filled it with 50% gray, and used the “Add Noise” filter to add 10 % Gaussian noise.

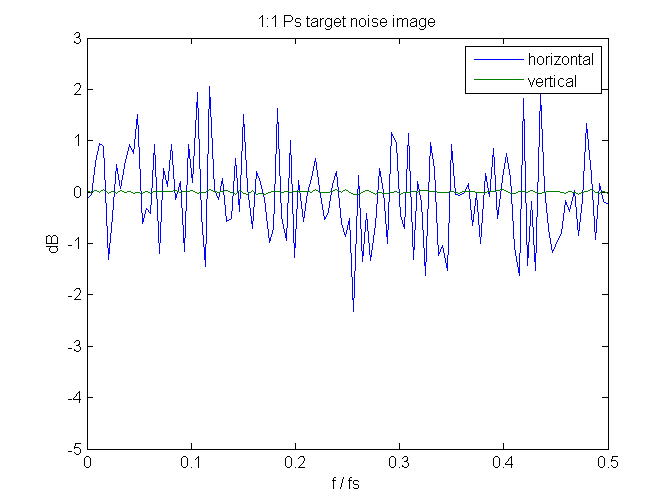
I downsized the image several different ways, and, as a check, looked at their spectra in Matlab. The spectra were jagged in one direction. I looked at the spectrum of the image that I’d created in Photoshop before downsizing:

The above is the spectrum of the image after conversion to linear representation.

That’s strange. The vertical spectrum looks fine, but the horizontal spectrum is jagged.

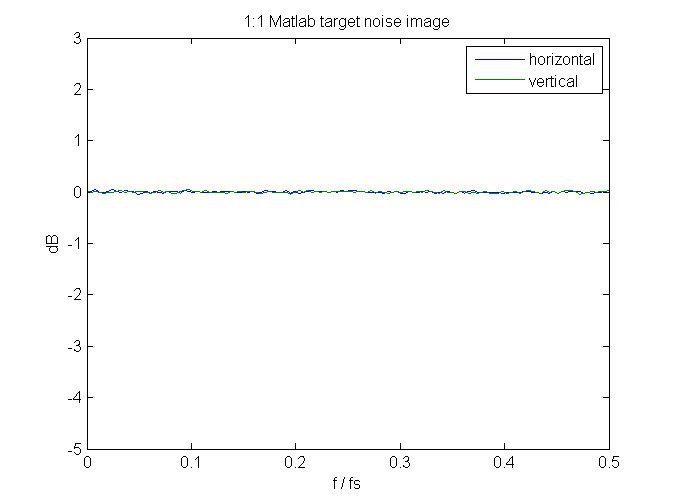
I created a similar image in Matlab, being sure to set the gamma to 2.2, and computed its spectrum in linear space:

All is well.

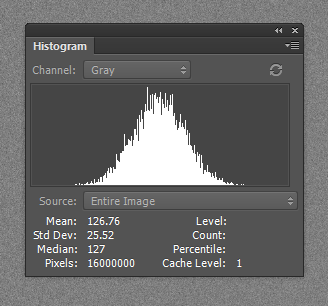
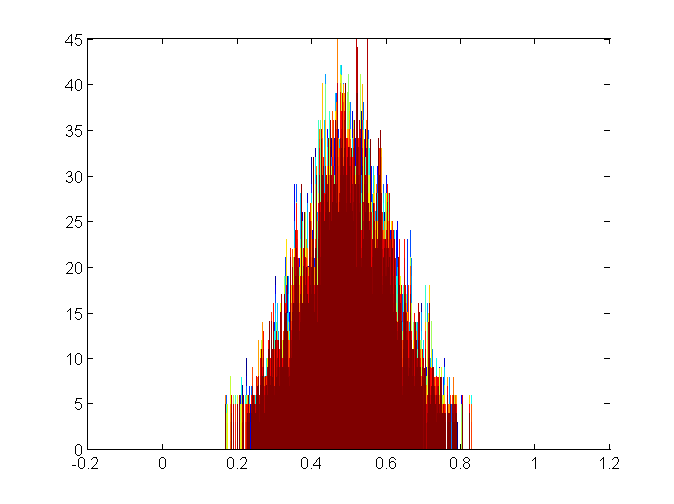
I looked at the histogram of the Ps-generated image in Ps:

and in Matlab at gamma = 2.2:

The Ps-generated shape seems wrong as measured in Matlab. The skirts don’t extend far enough, although the Ps histogram looks OK.

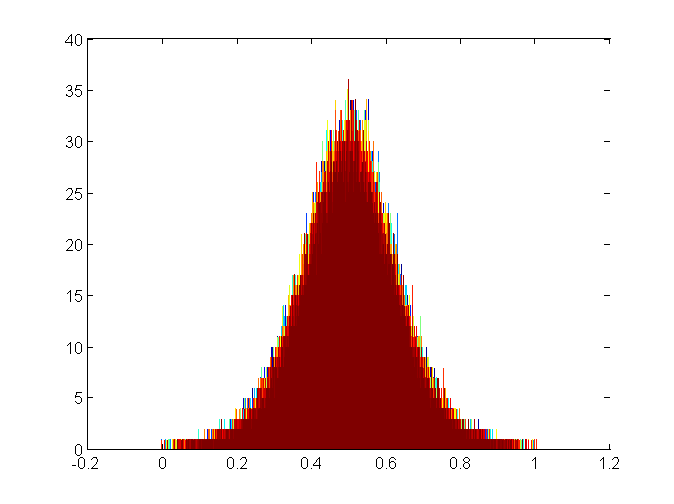
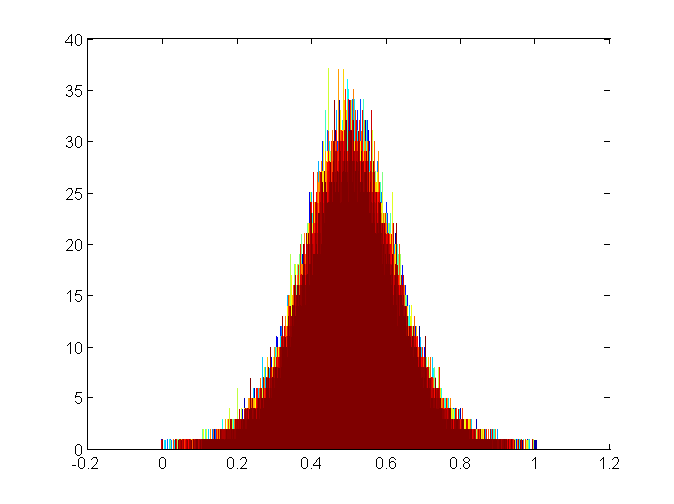
Here’s the histogram of the Matlab-generated image in Matlab at gamma = 2.2:

.

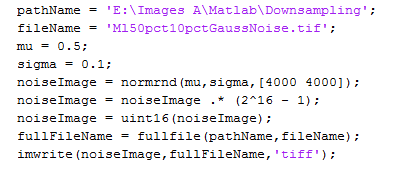
Then I generated the image in Matlab and wrote it to a file with this code:

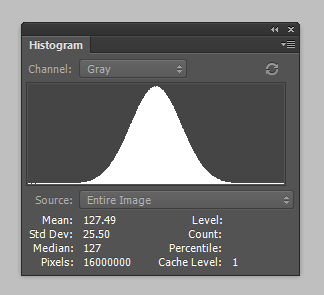
Here’s what the histogram looks like in Ps:

Compare that to the ragged histogram of the image generated in Ps:

Note that the mean in the Matlab-genetated image is 127.49. Perfection would be 127.5. The mean in the Photoshop-generated image, 126.76, is too low. The standard deviations in both images look OK as measured in Ps.

The problem is not in the way that Ps writes TIFFs or the way that Matlab reads them. Here’s a Matlab histogram of a Matlab-generated noise image after a round trip through Photoshop:

It looks fine.

I won’t be able to use Photoshop to generate the target images for my downsampling testing, or any other testing involving noise. I don’t trust it any more.

I don’t think these departures from Gaussian perfection should disqualify th Ps Add Noise… filter for normal photographic use, but I think they take it out of the running for measurements.