How focus-bracketing systems work

I’ve done a lot of testing of the focus bracketing (Fujifilm’s name for it), and focus-shift shooting (Nikon’s) on the GFX 50S, the GFX 100, the Z7 and the D850. I expected that the users of these systems would  be people who did focus bracketing or focus-shift stacking manually, and they wanted some way to automate the operation. Since those people would have to quantitatively understand depth of field/depth of focus/circles of confusion and be capable of moving back and forth between image and object space, I didn’t go into detail about how to use the features, and I used math that put some people off. By the way, if you want to bone up on geometrical optics as it relates to defocus image blur, read Chapter 3 of this paper.

I now realize that my original assumption about my audience was wrong. The availability of the focus shift features has given many folks whose knowledge of geometrical optics is weak the opportunity to try things that were previously only the province of experts, and those people are having a hard time putting my previous posts on the subject to work. This post is intended to explain how the systems work and how to use them with the following constraints:

• Assume nothing about the reader’s knowledge of the geometrical optics behind depth of field calculations
• Assume familiarity with the concept of depth of field
• Use minimal math
• Try not to introduce inaccuracies associated with simplifying complex concepts

Here goes:

The Nikon and Fuji systems all work about the same way, though the details vary. I suspect — but do not know for sure – that the focus shifting systems on other cameras are much the same.

Depth of field

First, let’s look at the problem these systems are intended to solve.

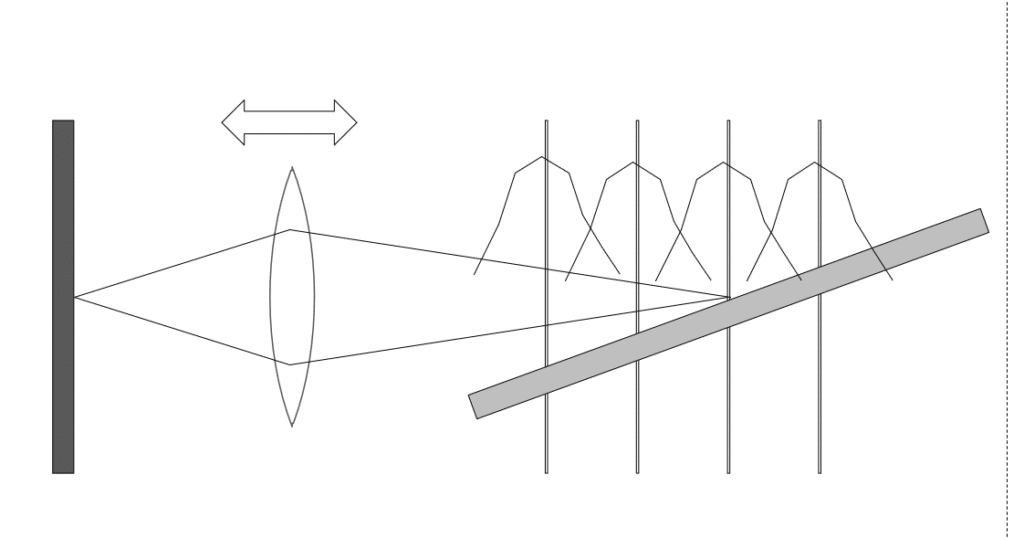
On the left, we have the camera. It is represented schematically by the sensor and the lens. The subject is on the right side of the sketch, and is a ramp rising as it becomes more distant. Focus bracketing or focus shifting (I will use the terms interchangeably) make successive exposures, moving the plane of focus between in each one. Nikon and Fuji both move the plane of sharp focus progressively further from the camera; others offer more possibilities. I’ve marked possible focal planes at four places with vertical lines, and I’ve sketched in how the sharpness might vary with distance at each location. Don’t put much stock in the precise shapes of those “haystacks”, but do understand that, for every focus metric that I’ve looked at, sharpness near the focal plane at first falls off gradually, then rapidly, then gradually again, as you move further away from the focal plane. That generality is correctly represented in the haystacks.

The extent of the haystacks is determined by the f-stop of the lens, and some other things that you won’t have to worry about (I’ll explain that later).

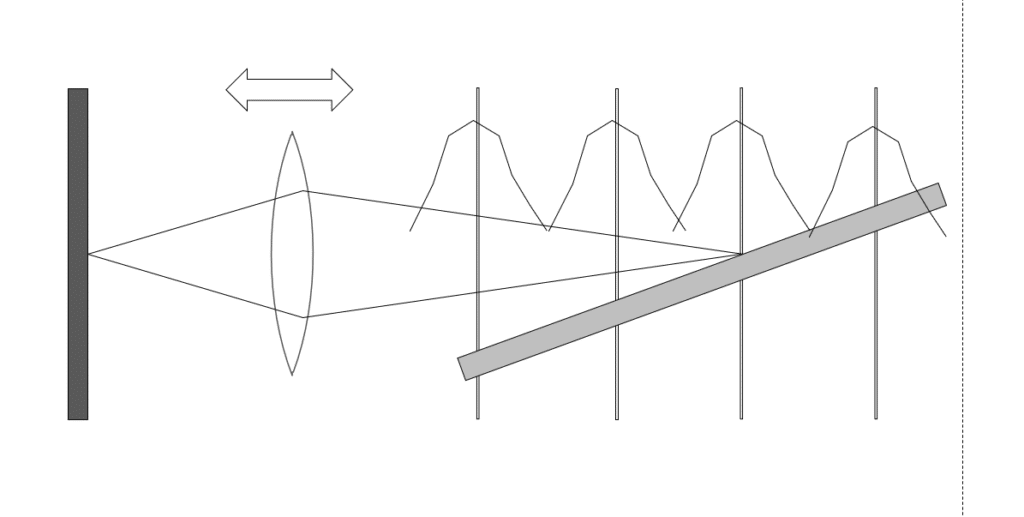
As the step sizes get bigger, the planes of focus become more separated, but the haystacks remain the same, with the result that there is progressively less overlap:

 

Note the places where the haystacks cross. The amount of sharpness at those points is the worst sharpness available in the completed set of captures.

Here’s the first rule of focus bracketing. All calculations of how big the step sizes should stem from deciding what the minimum acceptable sharpness is, and picking step sizes that are small enough to give you the sharpness you desire, and not so small that you waste a lot of exposures getting the job done.

Depth of focus

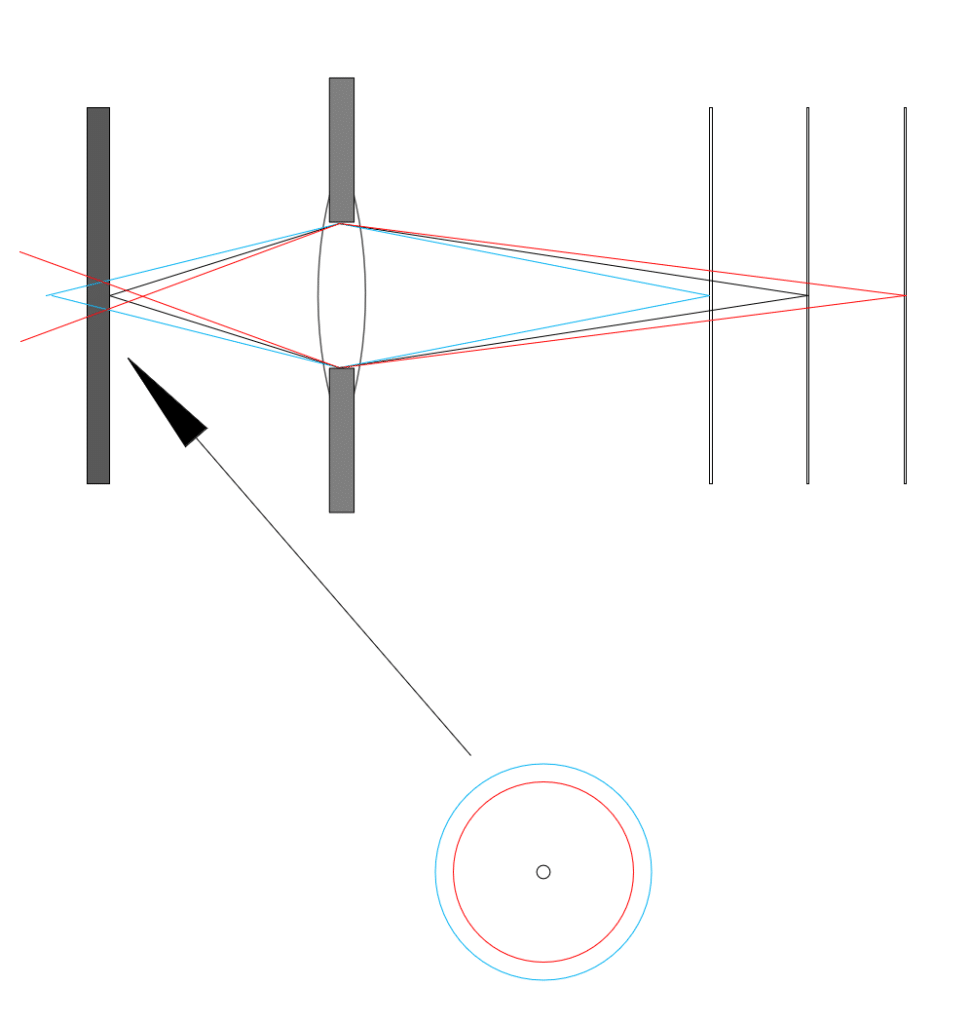
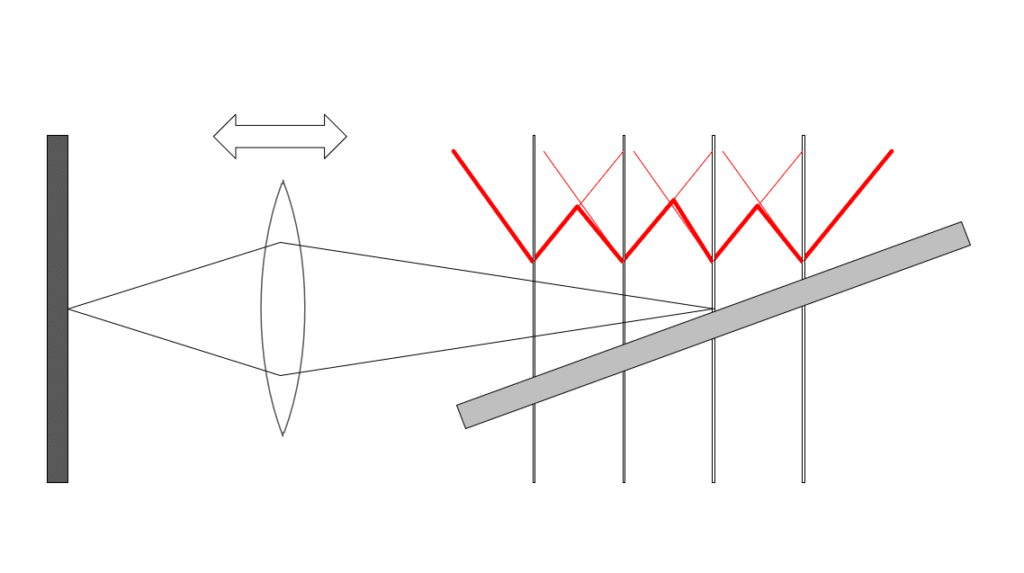
Now let’s leave the lens focusing alone, move the target, and consider what happens when the image on the sensor is out of focus:

 

The diaphragm is represented schematically by the two dark rectangles. The focal plane can fall ahead of, or behind, the sensor. When that occurs, we say that the lens is misfocused, or defocused (with respect to the subject). When the focal point is ahead of the sensor (the red lines), we say the subject is back-focused. When the focal point is behind the sensor (the blue lines), we say the subject is front-focused. When the image side focal plane falls directly on the sensor, we say the subject is in focus.

Image space and object space

There are two ways of looking at focus depth and defocus blur, as illustrated by the above. If we consider the effect on the object or subject side of the lens, we talk about object space and depth of field. Occasionally, people talk about subject space. Confusing the grammarians, it is the same as object space. If we concern ourselves with what happens on the sensor, or image side of the lens, we talk about image space and depth of focus.

Here is the second rule of focus bracketing systems like Nikon’s and Fuji’s: they work entirely in the image space. They don’t pay any attention to the focal length of the lens or the subject distance, although they do pay attention to the f-stop. And the surprising and wonderful thing is that, from the point of view of print sharpness, that’s all they need to do*.

Well away from the point of focus and near the lens axis, the blur circle of a normal (not apodized, not Petzval) photographic lens can be reasonably-well modeled by an image of the diaphragm opening. For most of today’s lenses, that means we’re talking about filled-in circles called circles of confusion (CoC). The thing that determines how much blur we’ll see in the image is the diameter of that circle. The size of the CoCs, which are illustrated in the lower part of the above figure. Note that no matter whether the image on the sensor is front-focused or back focused, the size of the CoC is determined by the amount of misfocusing on the sensor side of the lens (in image space).

Picking an acceptable CoC

In the film era, the CoC diameter was usually measured in millimeters. For 35 mm work, the diameter for the CoC that was used to construct depth of field tables was on the order of 0.03 mm. For critical work with today’s high-resolution digital cameras, that’s way too big. One way to get a handle on the size of a 0.03 mm CoC is to figure out how many such circles it would take to fill the height of a 35 mm landscape orientation frame. The answer is 720 circles. The vertical resolution of a high-res full frame camera is about 6000 pixels. You can see that you’re giving up a lot of sharpness if you use a 0.03 mm CoC to compute depth of field. These days CoC is usually measured in micrometers, or um. There are 1000 um to a mm. So, the traditional CoC diameter is 30 um. Sensor pitches for high-res cameras run around 4 um. For roughly equal contribution of sensor pixel aperture blur and defocus blur, you’d set the CoC for depth of field computations to about 4 um. That produces depths of fields that are much smaller (not paper-thin for normal circumstances, but going in that direction) than we’re used to seeing.

With a modern high-resolution camera, 30 um CoCs produce images that look pretty blurry. Depending on your subject matter, the size of your intended prints, and the esthetics of the scene, I recommend using 15 um as a default, and 7.5 um for the parts of the image that you want to look reasonably sharp.  If you want the most out of your camera, the right worst-case CoC for stacking and focus bracketing is on the order of the pixel pitch of the camera, or about 4 um for high-res cameras. If you want the ultimate precision, you could go as low as half that with modest improvement. For non-critical work, twice that will be just fine. 

CoCs in focus bracketed images

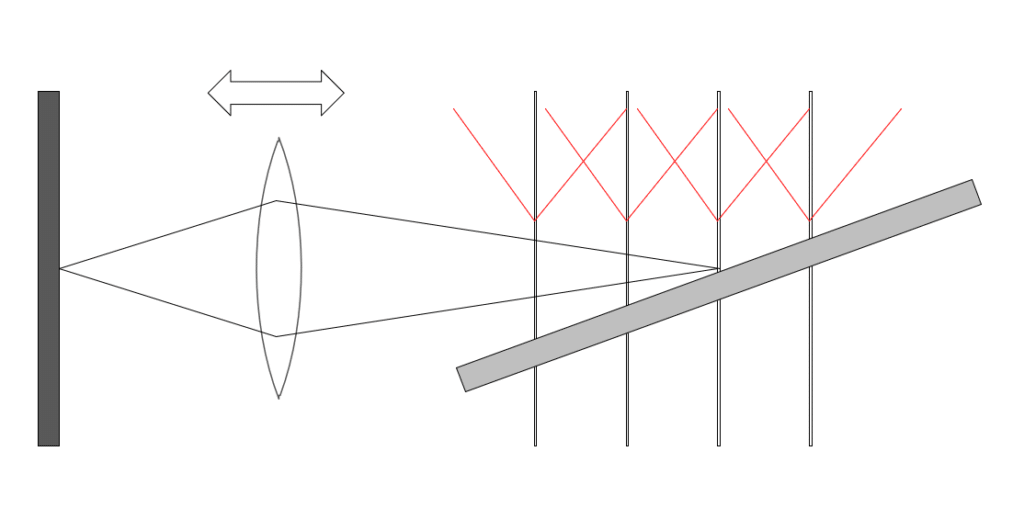
How do the CoCs affect the sharpness of our ramp? Let’s take a look:

I’ve drawn in red the way the CoCs for each of the four focused positions vary as you move away from those positions. Perhaps confusingly, I’ve drawn them on the object side of the lens, even though they exist on the image side. When I tried it the other way around, it was even more confusing. If you prefer, you can think of the red plots in the above image as the projection of the CoCs back into the object space, where they are called disks of confusion. In the each of the focused planes, the CoCs are zero (there will still be other sources of blur, such as diffraction and lens aberrations). As you move away from those planes, the CoC diameters increase approximately linearly (they do increase linearly in image space, but we’re looking at object space here).

The thick red line below shows the smallest CoCs that stacking software will see as it looks down the ramp:

Imagine you are the stacking software. Starting from nearer to the camera than the nearest focal plane, the CoC decreases as you move towards that plane, then widens again. When you get halfway to the second focal plane, it becomes sharper, and you can switch over to that image, and use it until you are halfway between the second and third planes, whereupon you can switch over to the image from the third plane, and so on until you reach the end of the captured images.

Similarly, if you as a human are going to select the image in which some object along the ramp is the sharpest, the biggest CoC you’ll see is half of the CoC seen in one plane when focused on the adjacent plane.

So, now you know how to pick a worst-case CoC for bracketing and stacking, and you know how the CoCs in your captures will affect the CoCs in your stacked image or in the image(s) that you manually select from your captures.

How the step size affects the CoC

The final piece of the puzzle is: when using focus bracketing, how do the shot-to-shot CoCs change with camera settings?

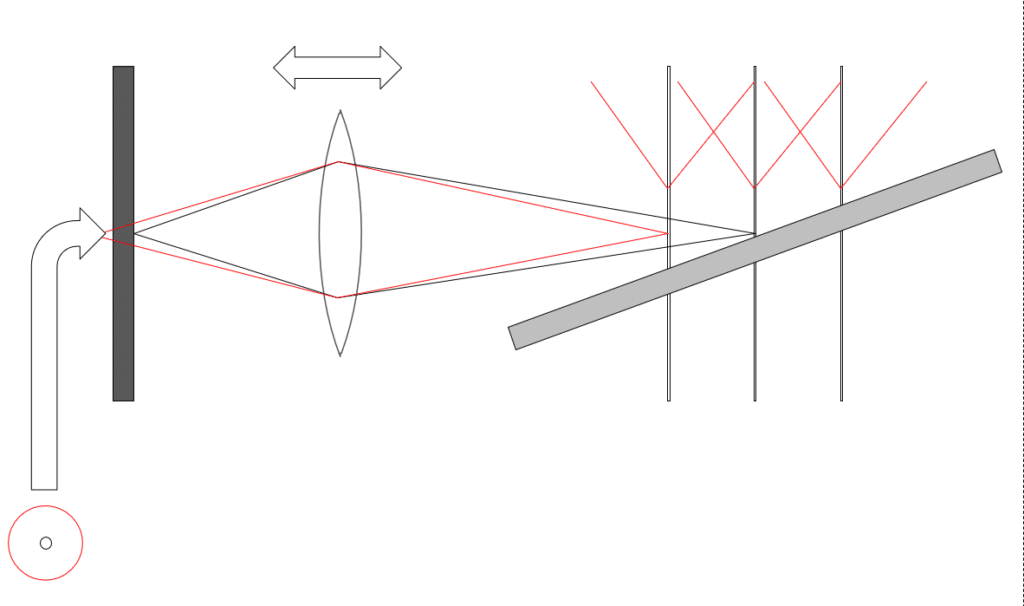
To deal with that question simply, we’re going to have to leave object space, and think like the camera does, in image space. The next diagram shows what happens when you focus on the middle plane, but examine the blur in the nearer plane.

The red circle indicates the blur circle in the sensor plane for an object in the near plane when the camera is focused on the middle plane. Let’s call that the single-step-CoC.  When you use focus bracketing, what controls its diameter?

The surprising answer is: just the step size. That’s right. Not the focal length of the lens. Not the distance from the camera to the subject. Not even the f-stop. The camera takes care of all that.

You don’t need to understand how the camera manages that feat to successfully use focus bracketing, but for those who are interested, I’ll explain now. The diameter of the blur circle is the shift in the image space focal plane from the sensor divided by the f-stop. The subject distance doesn’t enter into the calculations, since we’re working in image space. The focal length of the lens doesn’t matter, either, since it it handled by considering the f-stop. So all the camera has to do is look at the f-stop and the step size, and move the image side-focal plane so that the blur circle doesn’t change when you change the f-stop.

The beauty of this is that you can think of the step size strictly in terms of the blur circle that you are willing to have.

With the GFX 50 and GFX 100, it’s really simple: the single-step CoC in um is twice the step size, which means that the size of the largest blur circle you’re going to see in a stack from a set of captures (the worst-case CoC) is the step size in um. Step size = 1 means you’ll not need to use an image with CoC of over 1 um, which is ridiculously small for a 3.72 um camera. Step size of 4 means that the largest blur circle you’ll have to take is 4 um, which is about the pixel pitch, and not a bad place to start. With a step size of 10, you’ll have to use blur circles as large as two and a half times the pixel pitch, which is starting to get a bit sloppy. If you want to see the experimental results for the GFX 100, look here. Here are the GFX 50 experiments.

With the Nikon Z7, the minimum single-step  CoC is about 22 um (so the worst case CoC is half that), and step size 9 gets you about 200 um. There are some glitches that mean that sometimes, especially at  the lower step sizes, you won’t get the even step sizes that you should. Some experimentation will be required, but step size 1 will mean that the largest blur circle you’ll have to deal with is 11 um. Things get pretty coarse at the upper end: step size = 9 means you’ll have to be ready for blur circles as large as 100 um, which is pretty sloppy.

Putting focus shifting to work for stacking

With both the Nikon and the Fuji systems, the first step is to pick the step size based on your tolerance for blur in the stacked result. Then pick the near focal distance. Experiment to see how many shots will be necessary to get to the desired far focal distance, varying the f-stop if you wish (a narrower f-stop will require fewer steps; f/11 will require half as many steps as f/5.6.).** Once you’ve done this a few times, you’ll have a pretty good idea how many steps it will take. If the lens is longer or the subject is closer, it will take more steps. When you get really close, it will take a lot of steps, and you may wish to allow more blur by making the step size larger. At 1:1, image space is a mirror of object space, and the step size in the image field will be the step size in the object field; that means steps in the object field of a few micrometers.

An example

So let’s walk through how you’d plan for a shoot, assuming you have a GFX 100. Let’s say you are stacking images, using a program like Helicon Focus (my current favorite). Let’s further say that it’s a macro subject. Your first decision is the largest blur circle you’ll want Helicon Focus to have to deal with. You decide that you’ll be fine if it’s 6 um (which is a nice place to start if you have no idea), so you set the step size to 6. You focus a bit nearer than the closest thing that you want to be sharp, set the number of steps to a couple of hundred, and tell the camera to start making exposures while you watch the focal plane move in the LCD finder on the back of the camera (don’t use the EVF or you might jostle the camera). When the focal plane gets far enough away, note the number of exposures and stop the camera. Do you have too more exposures than you want to deal with? Stop the lens down a bit and try again. When you are getting about the right number of exposures, delete all your test images and start making real ones.

*One detail that is not reflected in the top drawing is that, in object space, the haystacks get broader as you get further from the camera, but the camera compensates for that by making the steps equal in image space, which means they get further apart as you get further away from the camera in object space.

**There are ways to calculate the number of steps required, but that requires a knowledge of geometric optics.