This is the 18th post in a series about the Leica Q2 Monochrom. You can see all the other posts in the series by looking in the Category List drop-down menu on the right side of the page.
I was asked to calculate the focal length of the lens in the Q2. I don’t have a Q2, but I do have a Q2M, and I’m going to assume that its lens has the same focal length.
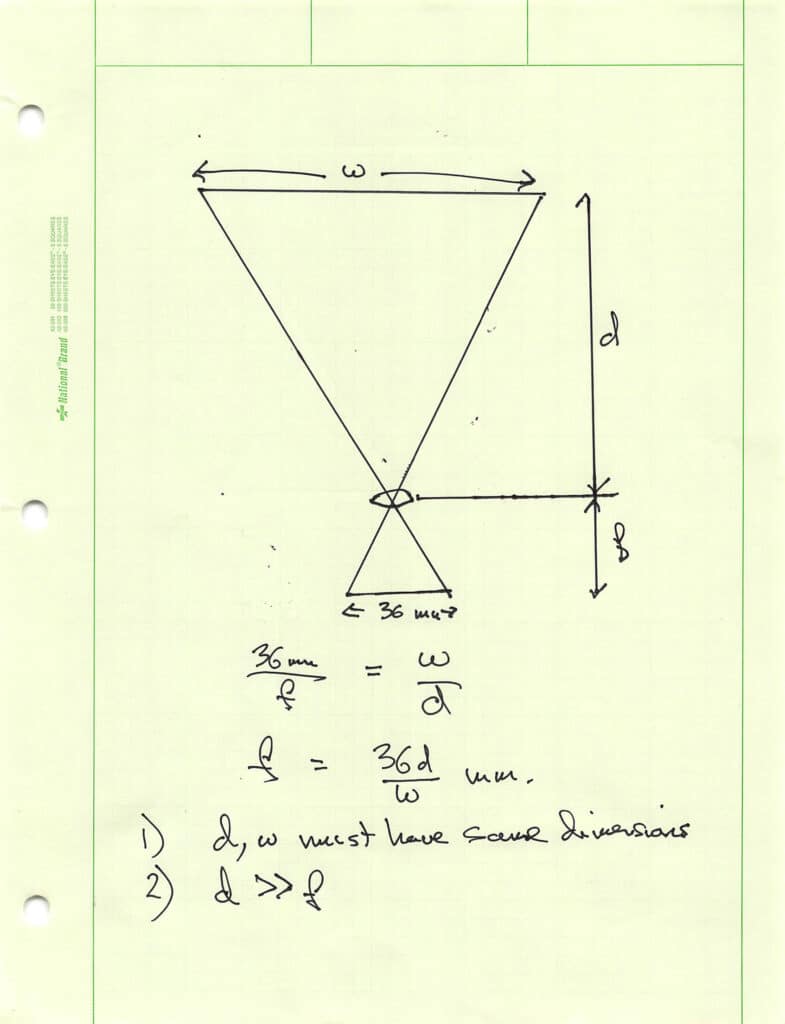
I came up with this method for calculating the focal length:
The method is based upon similar triangles on the object side and the image side of the lens. It depends on the lens being symmetrical, which is not true for the Q2 lens, but the differences should be small in this case if the target is far enough away.
Then I realized that, if the lens has significant distortion — which it does — I’d get an average focal length across the image field, but what I wanted was the focal length in the center of the field. So I decided to shoot a target that covered about a third of the horizontal width of the sensor. The rules of thirds grid in the camera made getting the target size in the frame about right. As you’ll see by the calculation to come, it doesn’t have to be exactly right.
I lined the camera square on to a garage door that’s 9 feet wide. I moved the camera back and forth until the garage door covered the central third of the image width in the finder. I captured a raw file. I measured the distance from the film plane to the garage door. It was 19 feet, 9 inches. I subtracted the putative focal length of the lens, and that gave me 19 feet 8 inches, or 19.67 feet.
I brought the captured image into RawDigger, and exported it as a TIFF, thus doing an end run around the software distortion correction built into Lightroom. I measured the extent of the door in the TIFF file with the Ps ruler: 2789 pixels. I measured the width of the image: 8376 pixels. Figuring that 8376 pixels is 36 mm, I calculated the width of the garage door on the sensor as 11.99 mm, which is pretty close to the 12 mm I was shooting for.
Then I performed the calculation above, replacing the 36mm constant with 11.99 mm. I got a focal length of 26.2 mm.
So, there’s your answer: 26.2 mm. After software distortion correction, the lens won’t appear to as wide and before, but it turns out that, with Adobe Lightroom and the default distortion correction, the effective focal length of the corrected lens is about the same as the uncorrected lens in the middle of the field: about 26 mm..
Hi Jim,
your method is good if we know the putative focal length of the lens,
but if we have no idea of its focal length we may transform the equation to get:
f = (36 x D)/(36 + W)
where D is the distance from the sensor plane to the target (d+f on your drawing)
and W is the width of the target.
By replacing 36 with w (sensor width) we get equation for all film formats
f = (w x D)/(w + W)
To simplify calculations all dimensions should be in mm
Making the putative focal length of the lens 0 only changes the results by 0.4% using my method, so it’s not a very important part of the calculation.
If you take a picture of the night sky and then send the file to https://nova.astrometry.net/upload
It will do fancy calculations and tell you the number of arc seconds per pixel which will give you another way to calculate the FOV. It will be in the log that is shown after solving but before you go to the solution.