This is the twelfth in a series of posts about the Nikon 70-200 mm f/2.8 S lens for Nikon Z cameras. The series starts here.
Yesterday, I told you about the quantitative differences that Imatest and I found between the Nikon 70-200 mm f/2.8 S and E lenses using a slanted edge and a Siemens Star target. Now I’m going to show you two more sets of results, one fairly conventional and one that I’ve never seen before.
The fairly conventional one is a contour plot of MTF contrast levels in polar coordinates by slice angle. Here’s what Imatest has to say about that plot:
The plot… shows MTF70 through MTF10 displayed in polar coordinates. Spatial frequency (cycles per pixel in this case) increases with radius. (This is the opposite of the image itself, where spatial frequency is inversely proportional to radius.)
This plot is most similar to the spider plot shown in Image Engineering digital camera tests and Digital Camera Resolution Measurement Using Sinusoidal Siemens Stars (Fig. 15), by C. Loebich, D. Wueller, B. Klingen, and A. Jaeger, IS&T, SPIE Electronic Imaging Conference 2007.
Here it is for the two lenses in the center:
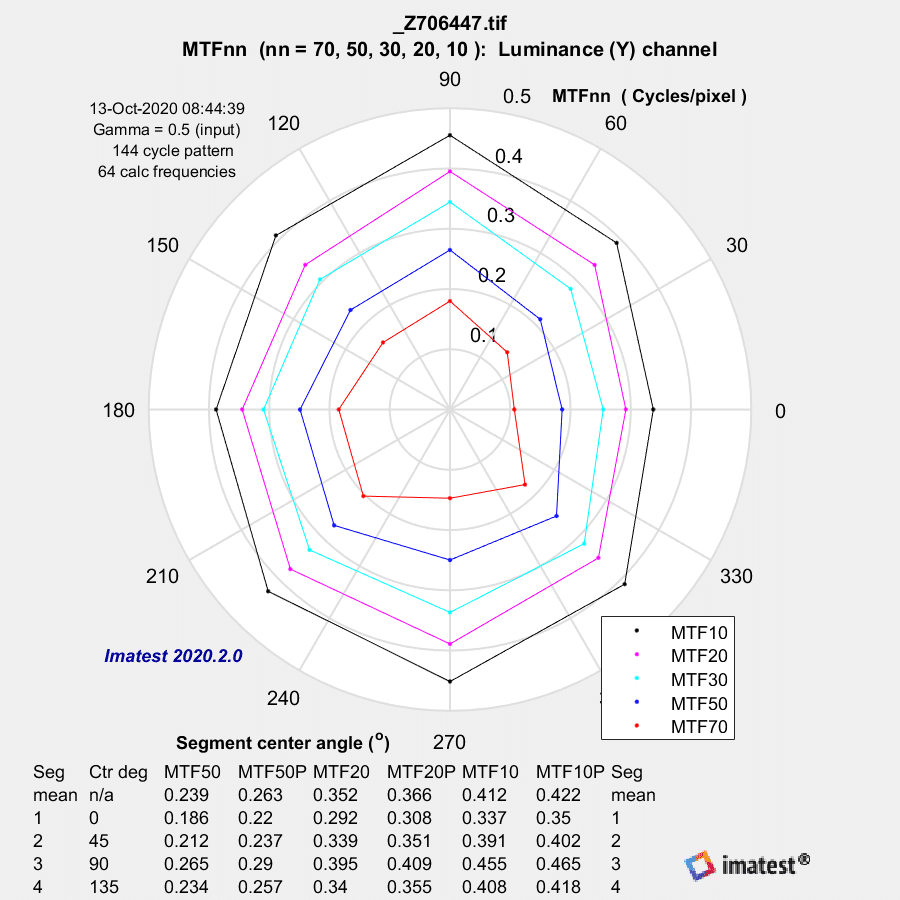

Those look similar.
In the corner:
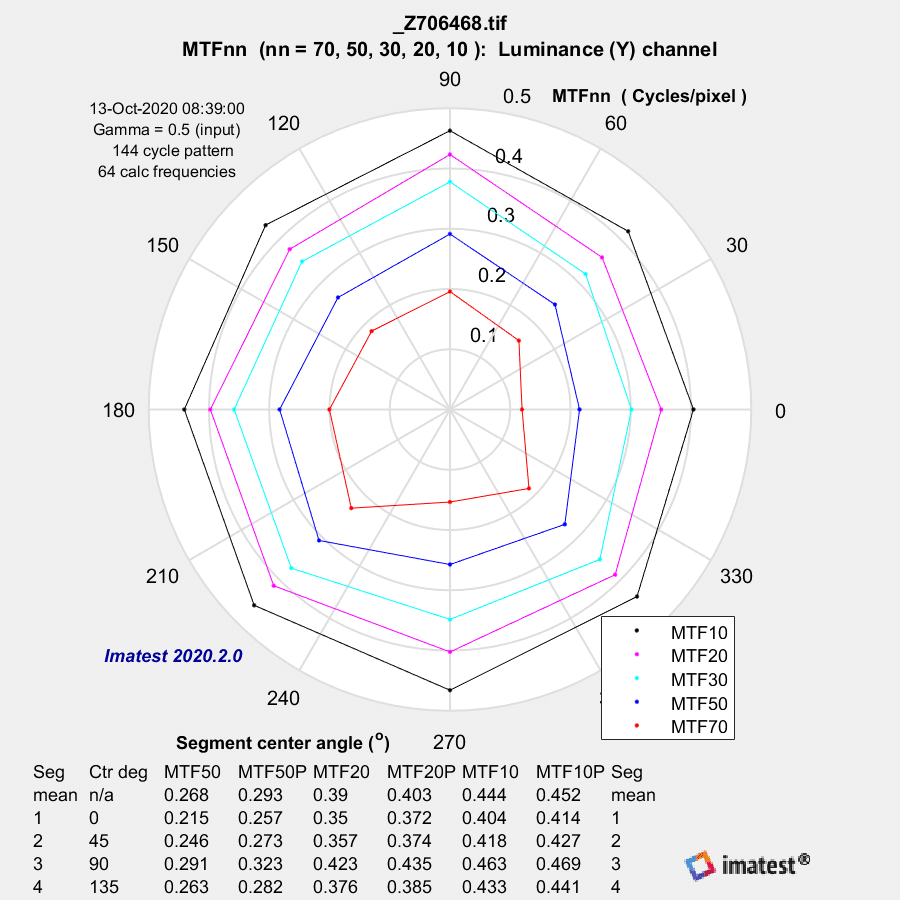
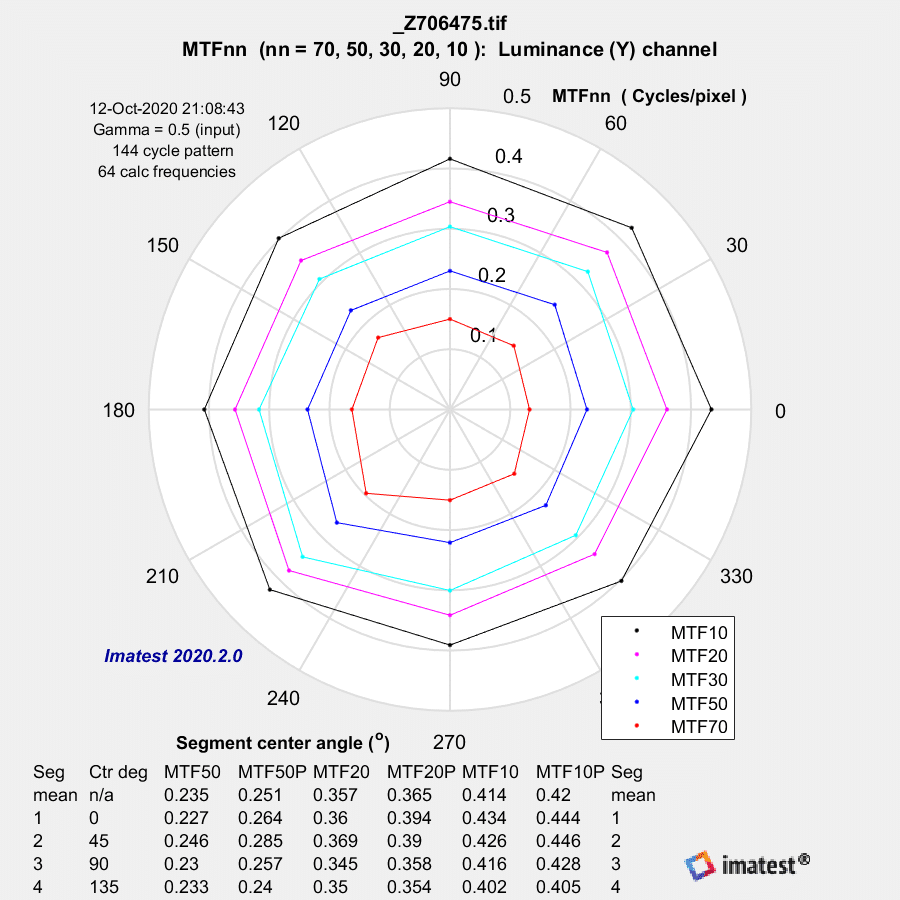
The differences are again not striking, with the E lens more symmetric.
Now for the novel approach. In this year’s version of their analysis program, Imatest has introduced a metric to gladden the heart of any computer scientist: the Shannon capacity. Here’s one of the plots associated with that metric.
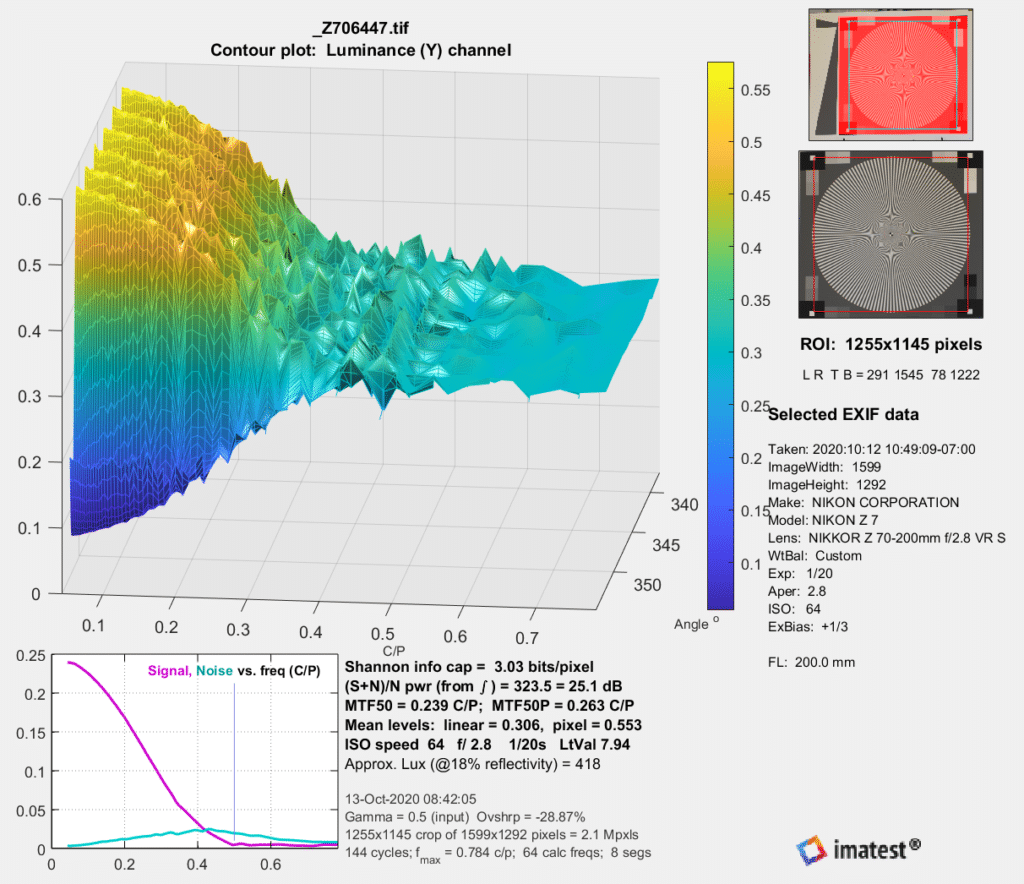
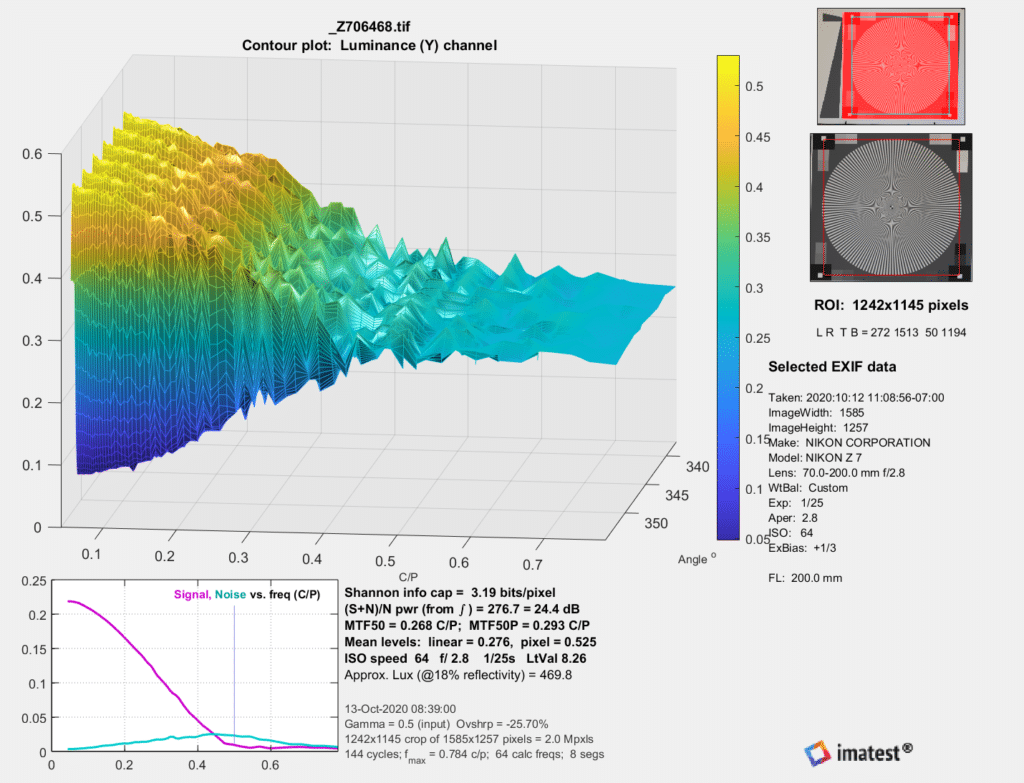
The information capacity of the S image is 3.03 bits/pixel, and that of the E image is slightly higher at 3.10 bits/pixel.
In the corner:
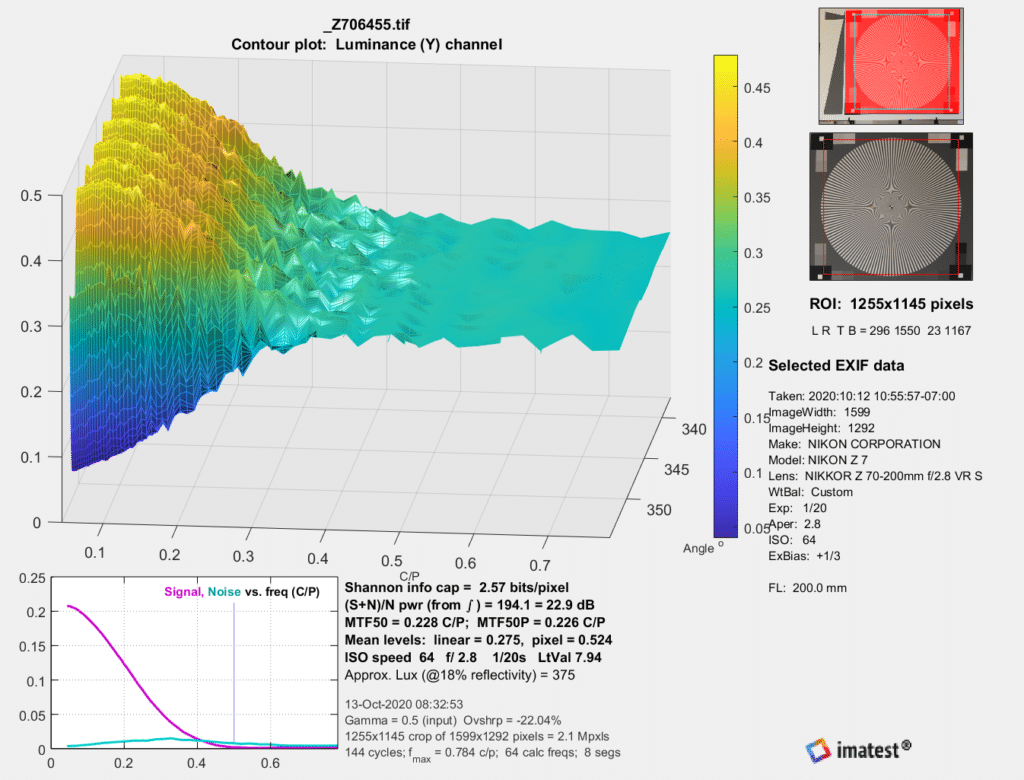
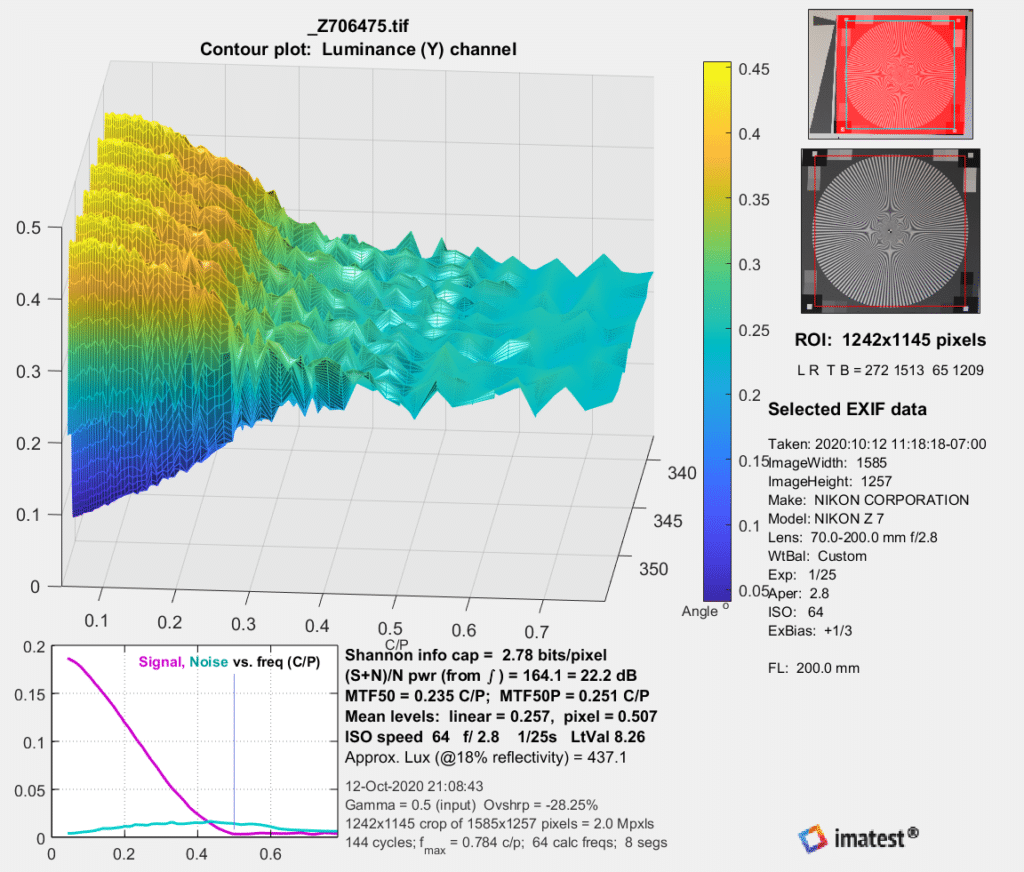
The information capacity of the S image is 2.57 bits/pixel, and that of the E image is slightly higher at 2.78 bits/pixel. Both are lower than the center images, which agrees with my visual impression.
It’s going to take some time to see how the Shannon capacity squares with image sharpness in general, but it is an interesting new metric.
A lot of thanks (again!) for your posts. A couple of comments for the Shannon part:
• I analyzed how Imatest converts ITS raw data (for dynamic range reports) to what it reports to the user. Their math is COMPLETELY wrong! (It seems that the code was written a decade ago, — and it has a good chance to work with 10-years old cameras! However, the assumptions they built in are majorly broken with the technology of today.) So one should be kinda careful with what they claim. (Of course, the situation may have improved, and their new code may be better.)
• It seems that the Shannon metric is not normalized for exposure. (This is correct — formally.) And your exposure is very different. Moreover, T-numbers may be quite different. So it may be that the reported Shannon metric is not reporting what you think it is reporting… (Cannot understand their notations, so cannot comment more.)
I’ve never used Imatests DR reports. Their slanted edge numbers are pretty close to MFT Mapper and my results using the Burns algorithm. I just started using the Siemens Star, and it more or less agrees with the slanted edge testing. Nice catch on the lack of normalization in the Shannon metric. Given the amount of light falloff, I guess that would invalidate center/corner comparisons, huh?
1st: I wrote “your exposure is very different” when I meant “your exposure is very different BETWEEN LENSES”. Sorry!
2nd: I did not even notice that you have center/corner comparisons! And: if you ARE interested in Shannon capacity at center/corner, then these comparisons WOULD make sense ;-] — but I doubt anyone would be so crazy. If you are not interested EXACTLY in this metric — then it seems pretty useless in any OTHER situation. (Kind of black/white without any gray scale in between…)
3rd: if you know what Imatest does with the slanted edges: what are red/green/blue curves on their graphs? Color channels vs. Y-channel?
4th: when I wrote my own slanted-edge evaluator, I saw A LOT of forks which would RADICALLY change the results. Are you processing RAW or de-Bayered picture? Is a pixel going to be represented as a δ-function, or a square? (Or, with monitors, as a 1×3 rectangle; or, with paper print, upscaled with an arbitrarily curve…) (This is what I remember how…)
So I cannot take your “numbers are pretty close” without a certain grain of salt…
Demosaiced by Lr.
Pixels are not little squares: http://alvyray.com/Memos/CG/Microsoft/6_pixel.pdf