There was a great thread on the dpreview forum started by Jack Hogan (who has also posted in this blog), about anisotropy in anti-aliasing filters. In the generally erudite and productive discussion that followed, someone (I’d give him credit, but I don’t know his real name) made these comments about demosacing:
From a reconstruction perspective, the numerical reliability of the interpolation of a Bayer scheme is dependent on how big the information holes are. If a point in the image plane has a very low numerical analysis accuracy probability, it is a “hole”. An unknown vector.
The size of the “hole” in the green map is the pixel width, plus the dead gap between pixels, minus the point spread function.
He then went on to say that the reason for the relative unreliability of the blue and red pixels was that their “holes” were bigger. I thought this was an interesting way to look at demosaicing, and incidentally, it’s what got me started thinking about the 2×2 (aka superpixel) demosaicing algorithm that I explored in the last three posts.
You can read the whole thing here: http://www.dpreview.com/forums/post/53492844
The poster then made the following off-hand comment:
Bayer makes the (correct) assumption that chroma data in a normal image has lower energy at high frequencies than luma data, so in most “image-average” cases this is a good tradeoff of interpolation accuracy. Lose a little bit of green channel (luma) HF and gain a bit of chroma HF stability.
That was news to me. I’d always thought that the emphasis that the Bayer array placed on green as a proxy for luminance was because human eyes are more sensitive to high-spatial frequency variations in luminance than they are to high-spatial frequency variations in chromaticity:
I posted my contention that the Bayer array’s oversampling of green was based on the way the eye worked, and the poster asked rhetorically how the eye got to be that way, implying that it was because the world was that way.
Well, you know me. I can’t let an assertion that seems counterintuitive go untested. I took the scene from the last post:
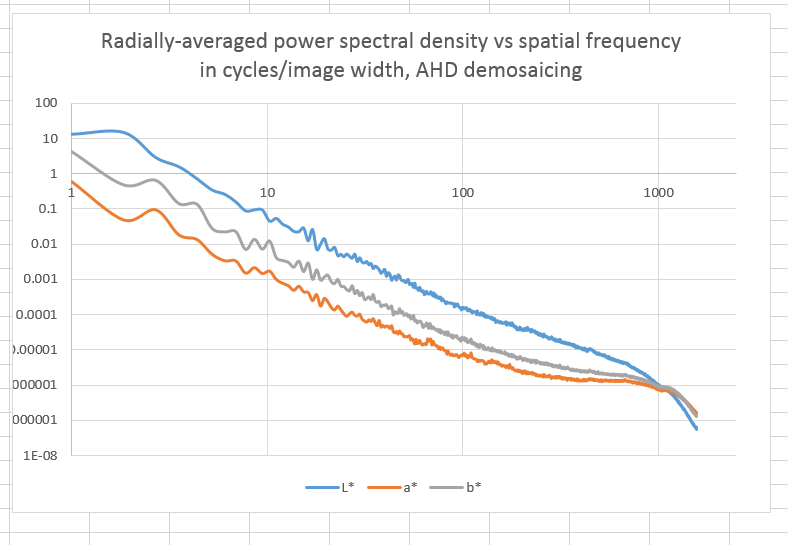
I demosaiced it with AHD in DCRAW, downsampled it to 50% with bicubic sharper, converted it to CIELab, took the 2D Fast Fourier Transform (FFT) of each plane, threw away the phase information by taking the absolute value, squared the result and normalized it by dividing by the product of the number of pixels in each direction. Then I computed a radial average to get a one-dimensional plot with the average of all possible directional power spectra in the image, and plotted that:
It doesn’t look like the chromaticity is rolling off any faster than the luminance at the highest spatial frequencies. In fact, if anything it’s rolling off a little slower.
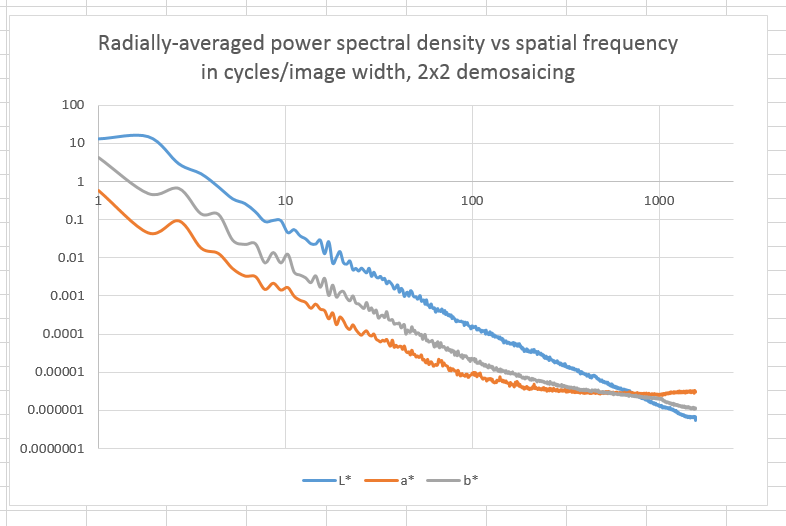
I also demosaiced the same raw file with the 2×2 method, and performed the same analysis:
There is even more high-spatial-frequency chromaticity energy now. However, I don’t think that’s real; I think it’s because the 2×2 technique creates more very small chromaticity errors.
That’s only one image. In order to gain some confidence, I’ll have to analyze a few more.


Leave a Reply