This is a continuation of a report on new ways to look at depth of field. The series starts here:
I’m going to leave the object-field approach for a bit, and continue on with refinements to the more traditional image plane methods, although I freely admit that I’m taking those methods to places their originators probably never intended.
A while back, I came up with a measure that I called the hyper-hyperfocal distance, which was a distance to set your lens to to allow for a degradation in sharpness at infinity equal to 10% of the MTF50 that you’d get if you actually focused at infinity. In other words, the hyper-hyperfocal distance allow retention of 90% of the sharpness available at infinity, in return for greater sharpness at distances closer than the hyper-hyperfocal distance.
Retaining 90% of the resolution is a pretty high bar, and the hyper-hyperfocal distances that I calculated were depressingly long.
Today, I’m going to generalize the concept, and drop the prefixing “hyper”, and talk about hyperfocal distances that are not based on the desired circle of confusion (CoC), but on the ratio of the MTF50 reduction at infinity to that obtained when focused at infinity.
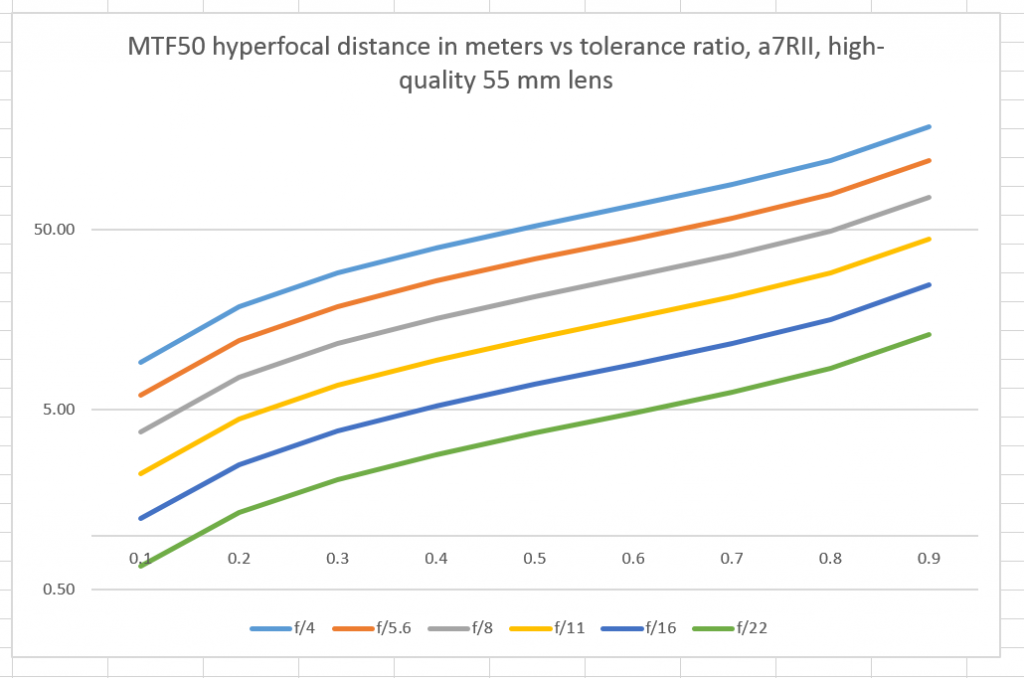
Without further ado, here is a set of curves for our top-notch simulated 55 mm lens on a Sony a7RII:
The way to use those curves in the field would be to decide on how much degradation at infinity you can tolerate, and find that ratio on the horizontal axis. Then run your finger upwards, and you’ll dee the hyperfocal distance for each f-stop.
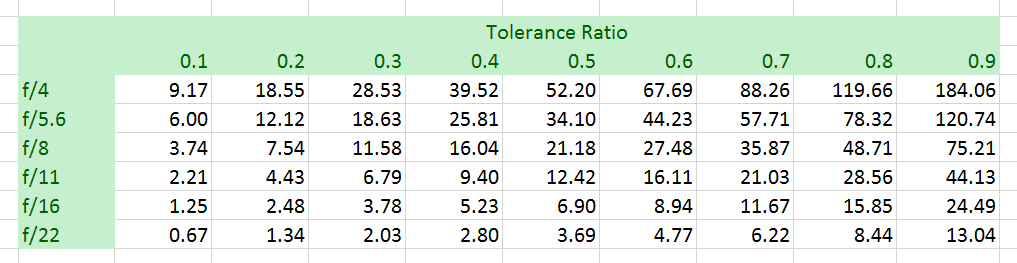
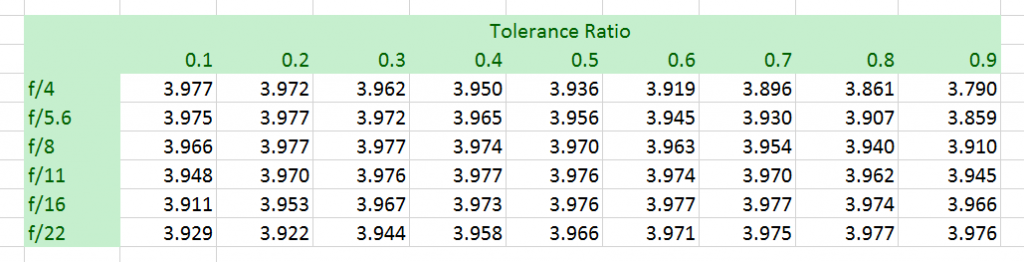
If you prefer tables, here is the data in that form:
Usage is similar: find the column corresponding to how much loss you can tolerate at infinity, and read the hyperfocal distances in meters for each aperture.
After a little prompting and some spot checking, I’ve been working under the assumption that, like CoC-based hyperfocal distances, these scale with the focal length squared. This provides an opportunity for more checking.
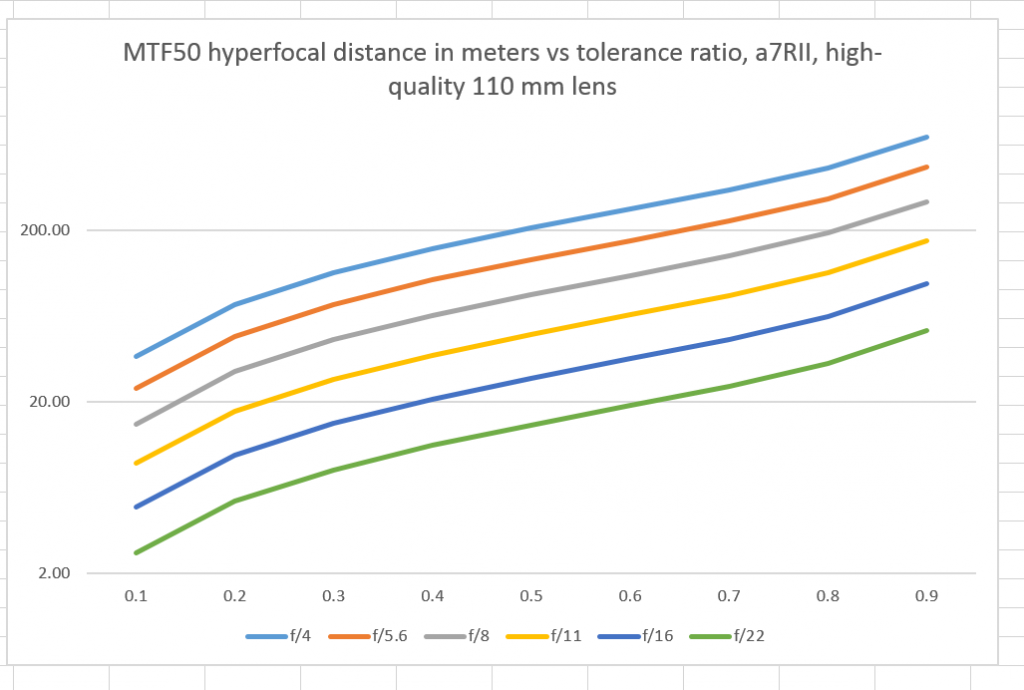
Running the modeling program with a 110 mm lens:
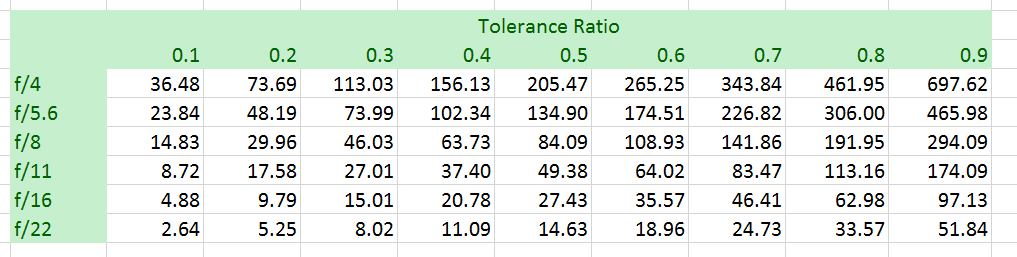
We see the distances are approximately four times the 55 mm case, as expected. But, if we calculate the ratios of the two tables, there’s a minor surprise:
Instead of the expected distribution on both sides of 4, there is a bias towards a lower number. I don’t know why that is, but I’m not going to worry about it for a while, if ever, since it’s so small.
When I was running these curves, I came up with a way to look at DOF that may be even more useful. Rather than bury it down her, I’m going to write a new post just about it.
The reason you do not get exactly 4 for the hyperfocal distance ratio for doubling the focal length has to do with short distance correction in the DOF calculations. In the standard formulas the far distance for DOF reaches infinity when f^2 = Nc(Do – f), where f is focal length, N is the f-number, c circle of confusion, Do object (or focus) distance. That extra f being subtracted from the object distance is what messes up the perfect square ratio.
I hear what you’re saying, Wally, but I don’t think that’s all of it, because the ratio varies with f-stop and threshold.
Jim