Yesterday, I presented material on how people’s ability to perceive small – and not so small – luminance changes varies with spatial frequency. Today, I’ll talk about how our ability to perceive changes in chromaticity (color without luminance) varies as spatial frequencies are manipulated. Yesterday, I started with the graphs and followed up with the visual demonstrations. Today, I’m going to reverse the order.
Exhibit A is an image that modulates between two CIELab values, 50,-35,0 and 50,35,0. Thus, L* and b* are held constant, and a* changes with a sinusoid that increases frequency exponentially (thus linear on log paper) from left to right, and reduces exponentially (thus linear on log paper) from bottom to top. If you back up a few feet and look at the places on the image where you can no longer make out the variations in color, you will get an idea of how your sensitivity to chromaticity changes along the a* axis varies with spatial frequency.
Exhibit B is the same idea, but a* is 0 throughout, and b* is varied:
In Exhibit C we go from one corner of the a*b* plane to the other:
Exhibit D is the other diagonal:
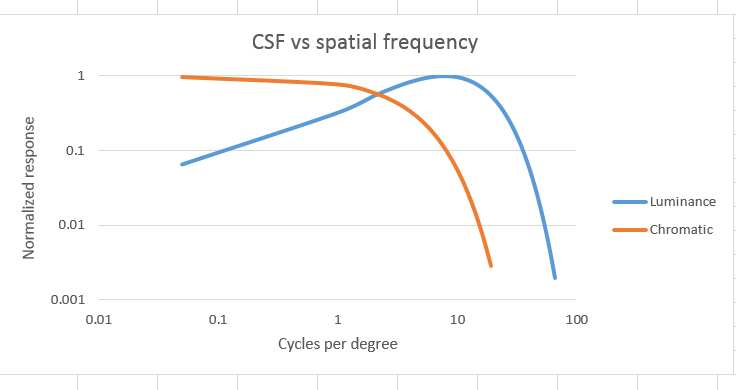
The sensitivity functions are not band-pass, as was the case yesterday with luminance. They are all low-pass, with the greatest sensitivity to change occurring at the lowest frequency. Not only that, but sensitivity falls more rapidly with increasing frequency than was the case with luminance changes.
In graphical form, with the luminance CSF curve for comparison, the chromatic CSF looks like this:
You can see that there’s no falloff in sensitivity for low spatial frequencies. You can also see that the lowpass falloff begins well before the luminance CSF peaks, and by the time that peak is over and the luminance CSF is starting to fall off with increasing spatial frequency, the chromatic CSF is way down there.
What’s that mean for photographers? We’ll look at that next time.


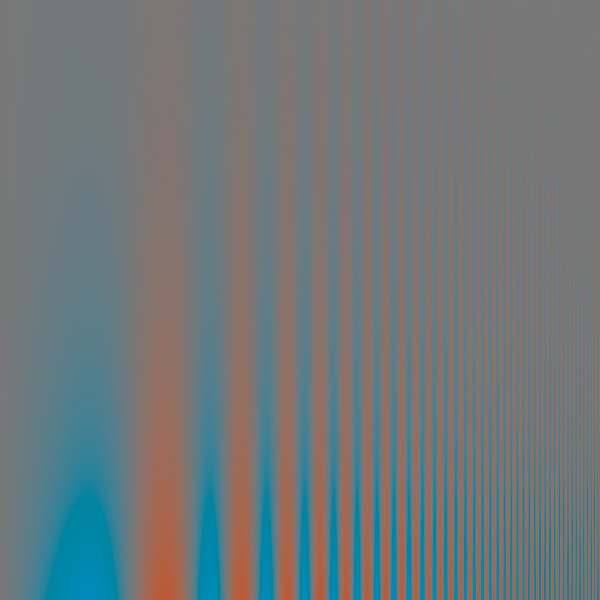

Leave a Reply