This is a continuation of a report on new ways to look at depth of field. The series starts here:
I’ve heard photographers say that sharper lenses — and cameras, for that matter — have less depth of field (DOF) than lesser ones. Is that true?
Like so many things, it all depends on the details of the question.
Let’s say you focus a lens at infinity, and measure the sharpness there as MTF50 measured in cycles per picture height (cy/ph). Call that MTF50Inf. Then you pick an acceptable MTF50 as a certain percentage (call that the tolerance ratio) of MTF50Inf, say 80%, call that MTF50Tol, and ask what distance you should focus to have the MTF50 for an object at infinity to equal MTF50Tol. That would give you a new kind of hyperfocal distance, similar in concept to the old, reliable, circle-of-confusion (CoC) based hyperfocal distance, but one that takes into consideration diffraction and lens aberrations.
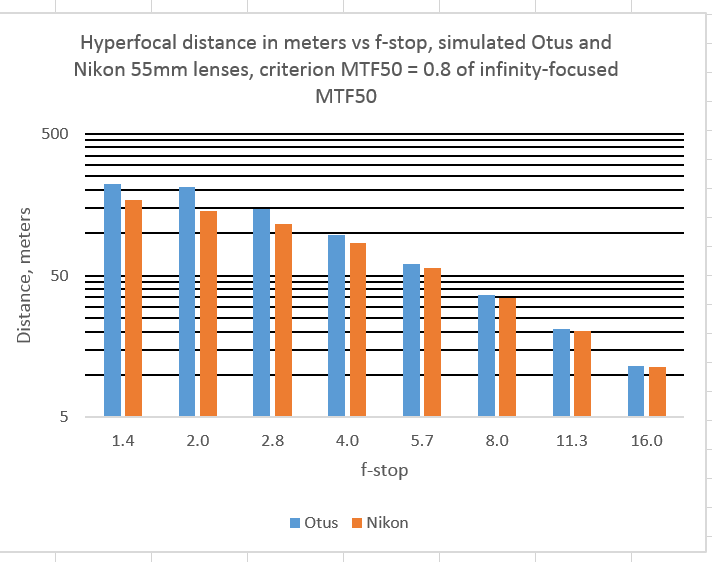
With our simulated Otus and Nikkor lenses, what would these hyperfocal distances look like? Here’s a set at a tolerance ration of 80%:
You can see that the hyperfocal distance using MTF50 ratios decreases as you stop down the lens, just like CoC hyperfocal distance. You can see that, from f/8 through f/16, it doesn’t make any difference which lens you use; that’s because in that range of apertures, in-focus sharpness is limited by diffraction, not lens aberrations.
You can also see that, at the wider apertures where aberrations play a bigger role than diffraction, that, yes indeedy, the sharper Otus does have less DOF, as indicated by the longer hyperfocal distances.
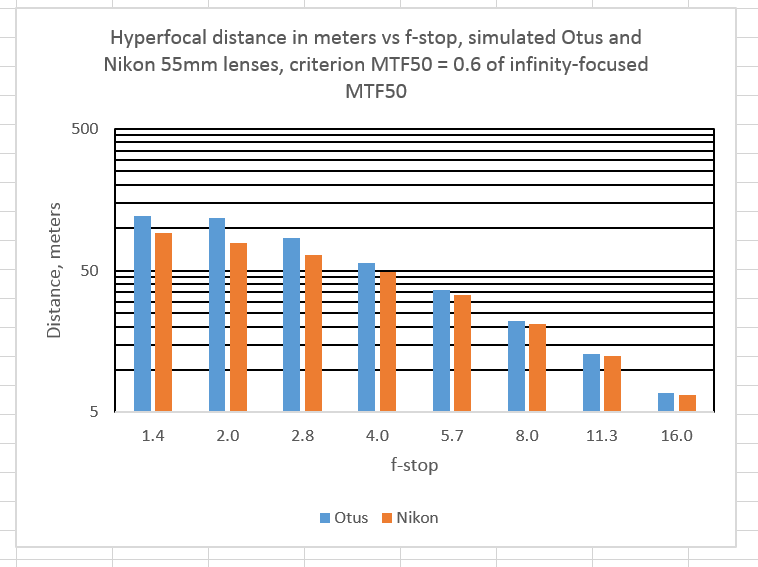
At a tolerance ration of 60%:
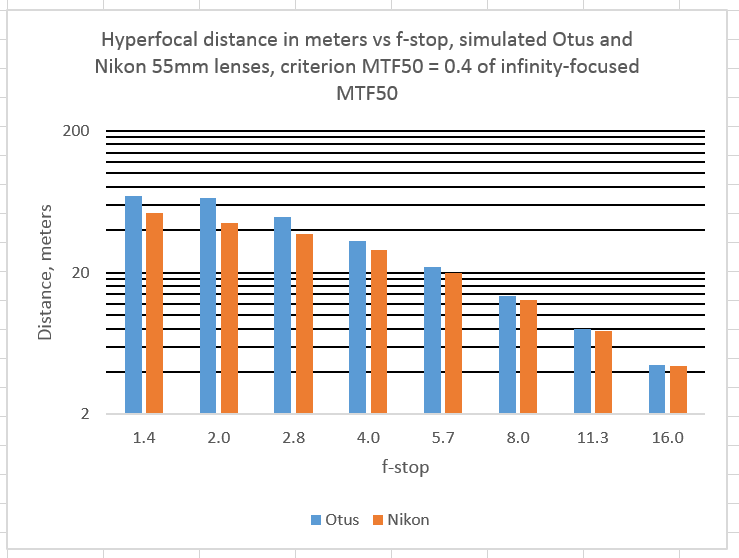
40%:
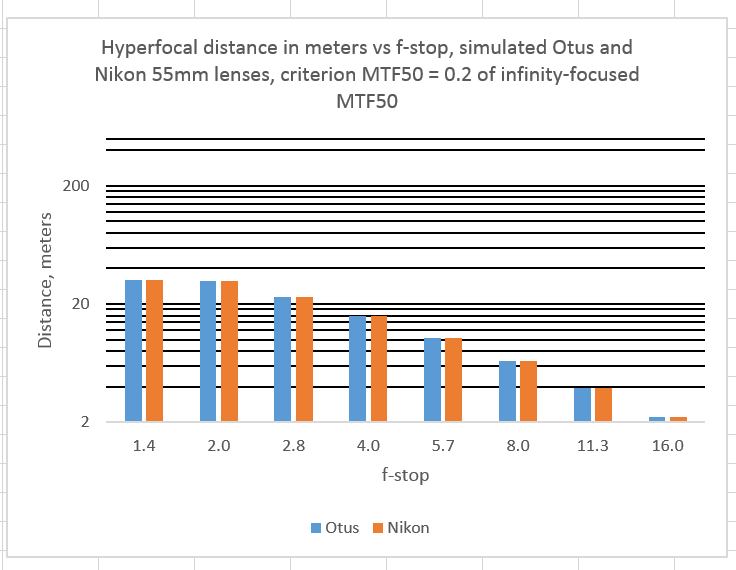
And finally, 20%, which is getting downright fuzzy:
At 20% tolerance ratio, the quality of the lens doesn’t make much difference a any f-stop, but at 40% and up it does.
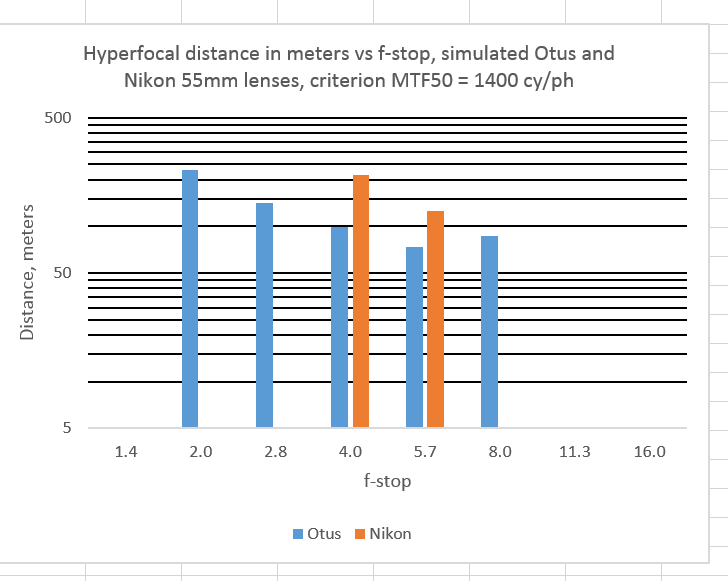
Now let’s say that the boundaries of our acceptable DOF are determined by an absolute MTF50, say 1400 cy/ph.
Then we get:
By that measure, the Otus has more DOF than the Nikon, which doesn’t even get to the bar at any distance at three f-stops. BTW, neither lens gets there at f/11 and f/16, because of diffraction.
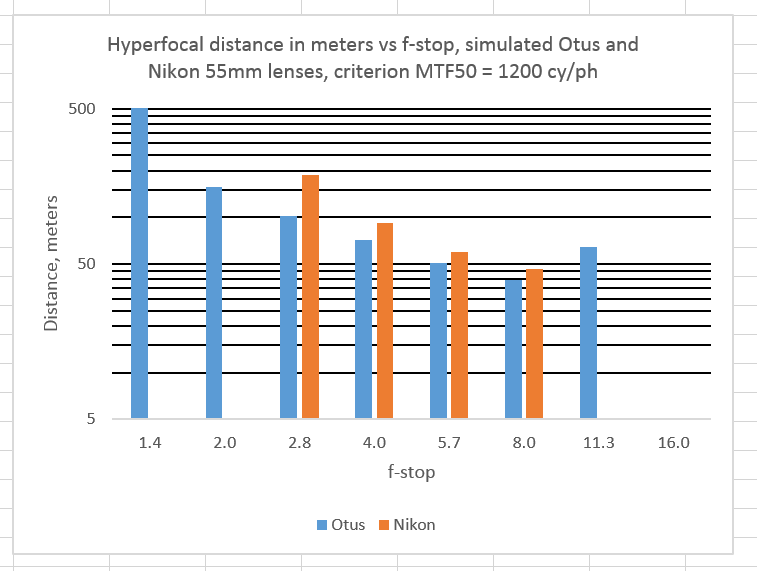
If we lower the bar to 1200 cy/ph:
Yup, the sharper lens has more DOF by that measure.
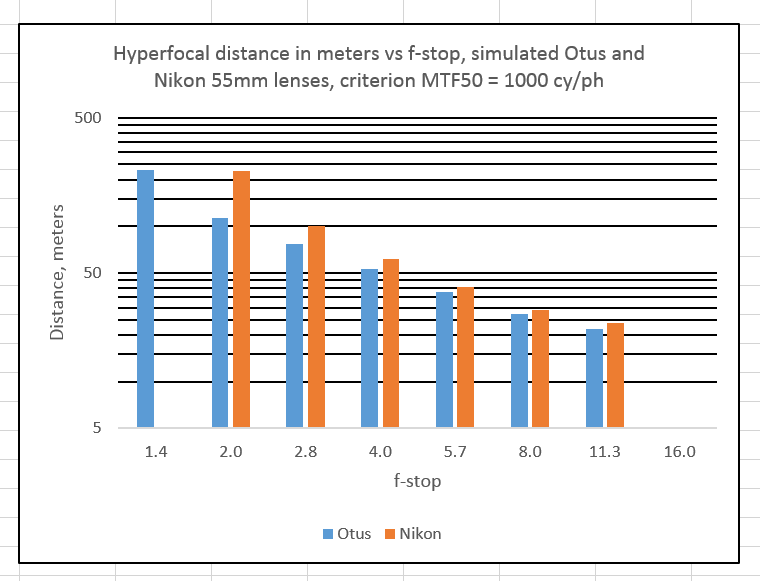
At 1000 cy/ph:
And finally at 800 cy/ph, where we finally get all f-stops represented:
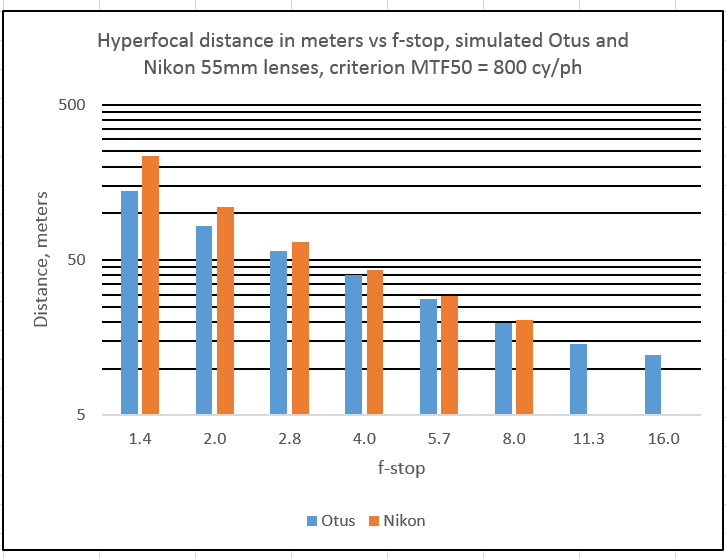
That was pretty much what I expected.
The question is now to conduct a double-blind study of images taken of various scenes, set to the optimal aperture and focus distance determined various hyperfocal distance criteria, with various display methods (different screen resolutions, different print sizes) and ask a collection of people whether they’d consider something to have deep enough depth of field or not.
When you’re finished with that, I’d like to have a look.