In the last post I showed MTF results from a simulation of a Bayer-CFA camera with a diffraction-limited lens. The camera had a 4.77 micrometer (um) pixel pitch. I had previously done an MTF analysis of the Zeiss Otus 55mm f/1.4 lens on a Sony alpha 7R, a camera with that pixel pitch.
I thought I’d try to model the MTF vs aperture of the real lens. I used double application of a pillbox (circular) kernel, with radius equal to:
R = k1 + (k2 / fstop)
Where the constants k1 and k2 were selected for the closest match between the model and the real lens.
I changed the simulation to compute MTF based on luminance, assuming 650 nm light for the red plane, 550 nm light for the red plane, and 450 nm light for the red plane. Since I’m modeling and Adobe RGB sensor, luminance is 0.31111 * R + 0.62527 * G + 0.06322 * B.
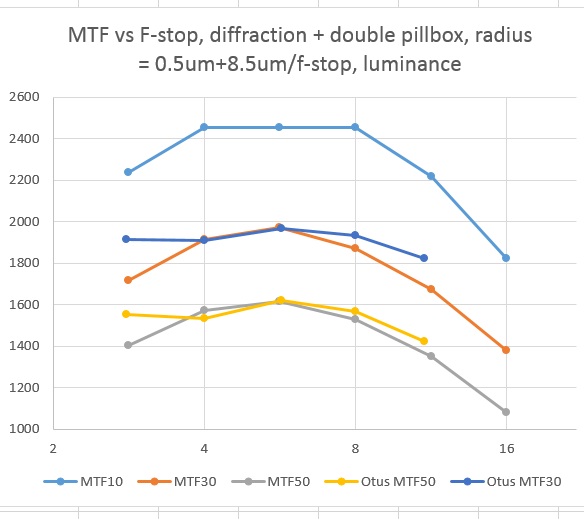
I plotted MTF50, MTF30, MTF10 for the simulated camera and lens, and the first two for the real camera and lens. The match is fair:
The reason why the MTF10 line flattens at the middle f-stops is that I didn’t allow the MTFs to exceed the Nyquist frequency, figuring that any energy above that frequency is useless at best. You will notice that the real lens does better than the model. There are differences in the way that the MTF curves for the real and simulated setups the real images were demosaiced by Lightroom, using their “secret sauce” and the simulated images were demosaiced using the less-sharp bilinear interpolation.
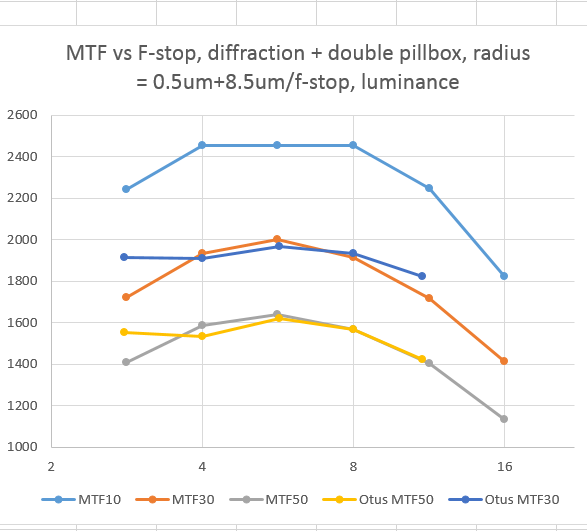
By the way, the above were calculated with a kernel for diffraction simulation three times the diameter of the first Airy zero. I tried to save some computer time as use a kernel twice the diameter of the first Airy zero and got this, which is visibly not as accurate (that is to say, different) from f/8 on up:
Leave a Reply