[Note. The bilinear and bicubic interpolation algorithms referred to in this article are the Matlab implementations. They are different from the Photoshop algorithms of the same or similar names. The Photoshop versions are reported on a few posts further on. Therefore, this post is primarily of academic interest.]
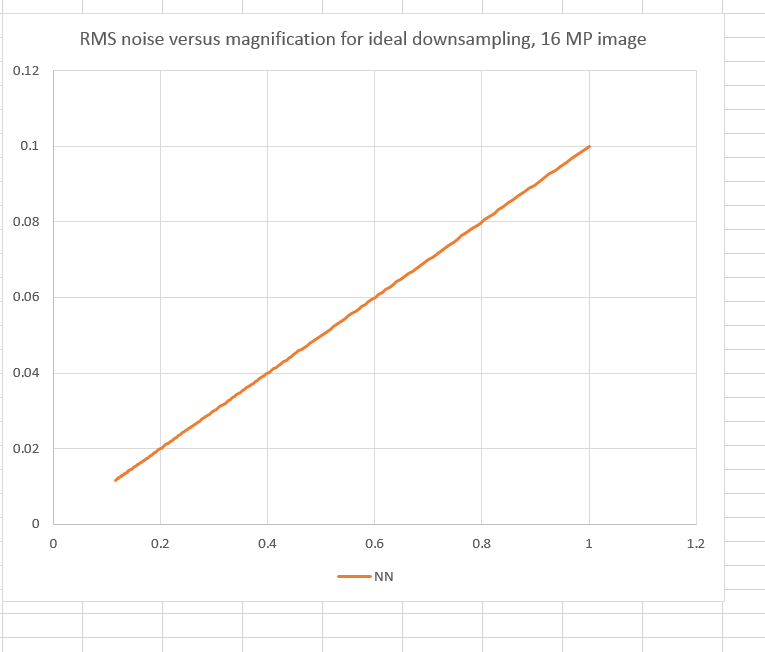
It is axiomatic in photography that photon noise decreases upon downsampling in direct proportion to the magnification ratio — the width (or height) of the output image over that of the input image.
Downsampling by a factor of two should cut the noise in half. That’s what would happen if you averaged four input image pixels for every pixel in the output.
This reasoning is one of the bases for photographic equivalence. It’s at the root of the way that DxOMark compares cameras of unequal pixel count. It’s accepted without much thought. I qualify my statement, because there are some who don’t buy the notion.
It’s clear to me that binning pixels — averaging the values of adjacent captured pixels before or after conversion to digital form — will reduce photon noise as stated above, although the two operations have different effects on read noise. What’s not clear is how good the standard ways that photographers use to reduce image size are at reducing noise.
I set out to do some testing. I wrote a Matlab program that I’ll be posting later that created a 4000×4000 monochromatic floating point image, and filled it with Gaussian noise with a mean of 0.5 and standard deviation of 0.1. I then downsampled it using various common algorithms: bilinear interpolation, bicubic interpolation, Lanczos 2 and Lanczos 3. at 200 different output image sizes, ranging from the same size as the input image to less that 1/8 that size in each dimension.
Then I measured the standard deviation of the result. That’s the same as the rms value of the noise. If downsampling operates on noise the way that photographic equivalence says it does, then we should get curves that look like this:
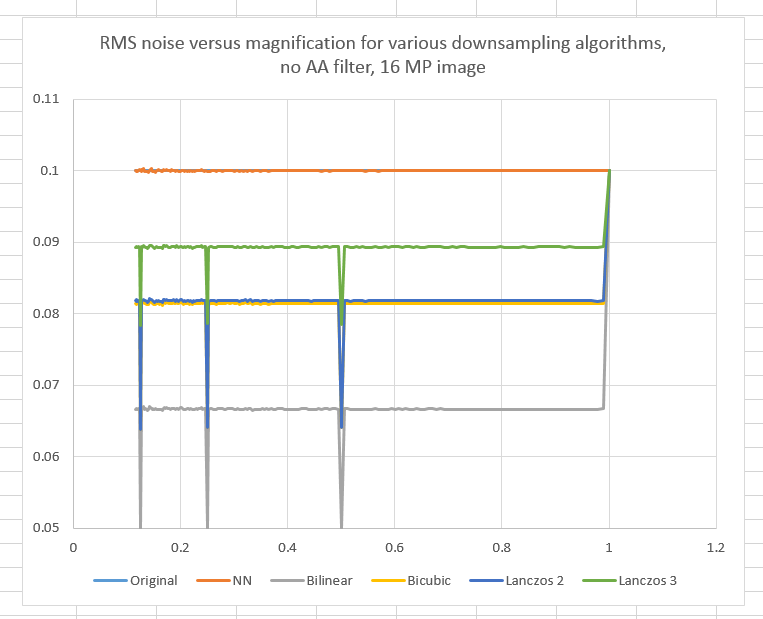
But that’s not what happens. Instead, our curves look like this:
Whoa! Except for some “magic magnifications” — 1/2, 1/4, and 1/8 — the noise reductions are all the same for each algorithm. Bilinear interpolation is the best; it hits the ideal number at a magnification of 1/2, and the sharper downsampling algorithms are all worse. None of the algorithms do to the noise what we’d like them to do.
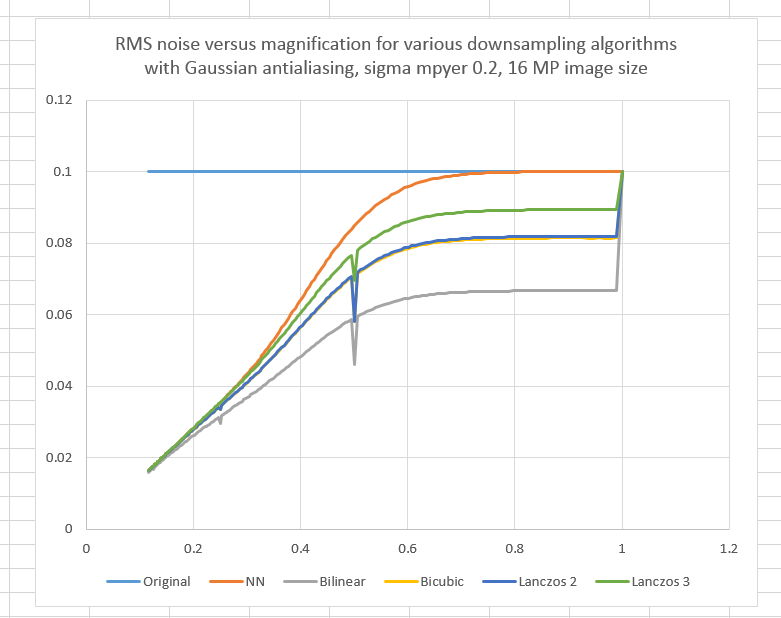
Bart van der Wolf is a smart guy who has looked extensively at resizing algorithms. One of the things he recommends is subjecting the image to be downsampled to an Gaussian anti-aliasing (AA) filter whose sigma in pixels is 0.2 or 0.3 over the magnification.
Here’s what you get with a AA sigma of 0.2/magnification:
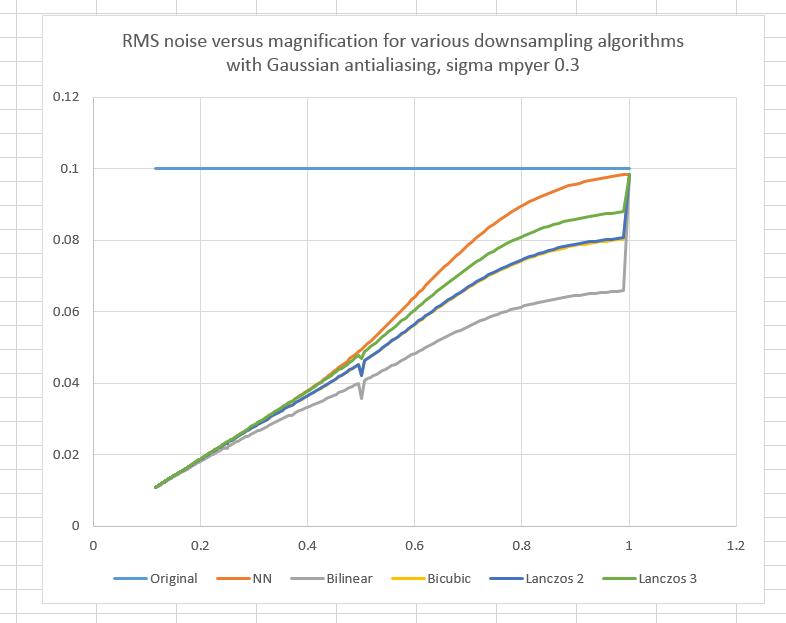
And here are the curves with sigma equal to 0.3 / magnification:
Well that’s better. With 0.3 / magnification, by the time we get to 1/4 size, we’re pretty much on the ideal curve.
But what does the AA filter do to image detail? Are the downsampled noise images still Gaussian? What would happen if we downsampled in a gamma-corrected color space? What about the demosaicing process? What do these algorithms have to do with the ones built into Photoshop and Lightroom?
Stay tuned.
It’s unfortunate that Eolf’s site is gone and with it all that was published.
That’s true. I have removed the now-broken link. Thanks.
The previous broken link appears to have already been to the Wayback machine but just the wrong date to capture Bart’s page before it disappeared.
This Wayback link is referenced to about when the blog post was originally written and Bart’s page was still active and archived then:
http://web.archive.org/web/20141027051036/http://bvdwolf.home.xs4all.nl/main/foto/down_sample/down_sample.htm
Nice article, can you share the 4k image please?
I no longer have the originals. It’s been seven years.