This is a continuation in a discussion of spatial frequency response (SFR) and modulation transfer function (MTF) testing reproduciblity. The series starts here:
This post is a continuation of the last one in this series:
The thrust of that post was that moving the target rather than the camera had the potential of making practical off-axis LoCA and focus shift testing by changing object distance.
A problem that I ran into in trying to turn theory into practice was that small alignment errors made the razor blade’s position in the frame not constant throughout the series. One way to deal with that is to black out the perforations in the razor blade with tape so that the region of interest (ROI) can be larger and MTF Mapper won’t get confused by edges other than the one I want it to look at. I will do that in future tests, but I didn’t for the work reported here, figuring that If I could programmatically deal with a moving razor blade with holes in it, blacking out the holes would only make things simpler.
The way I dealt with the target’s motion in the frame has a long tradition in engineering: even if you know something is nonlinear, assume it is linear and see how far you can get.
I set up the program so that it knows how many images there are in one series, a series being defined as a sequence of images in which only the target position changes. It presents the first image and the last image in the series to the user (moi), and asks him to pick the location of the ROI. Then it runs the whole series, linearly interpolating the location of the ROI between the two end points.
Why did it take me several days to make a change like that? While I was at it, I took the opportunity to reorganize the program, to report its progress in a way that I don’t waste a lot of time getting an incorrect result, and make it more tolerant of cases where MTF Mapper can’t make sense of a particular image. I consider that time well spent, since it will make future modifications to the program easier. In this context, let me express my thanks one more time to Jack Hogan, who wrote the Matlab code that I started with.
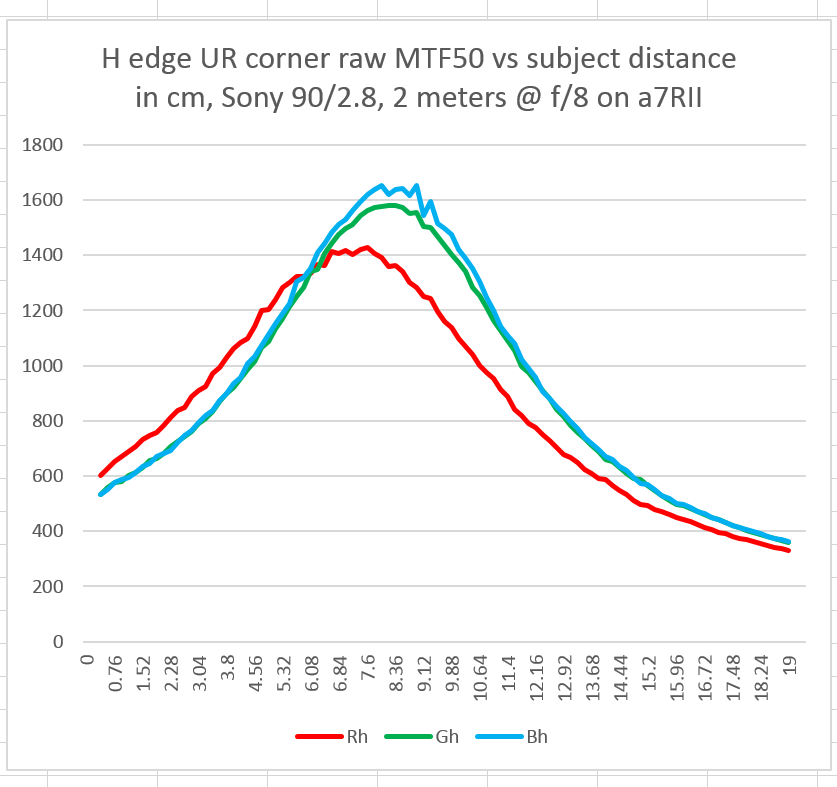
Let’s look at the longitudinal chromatic aberration (LoCA) in the upper right corner of the frame, with the Sony 90mm f/2.8 FE macro lens at f/2.8 with the target nominal (center of the horizontal axis of the graph) at approximately 2 meters:
Distance is the horizontal axis, with the left hand size having the subject farther from the camera than the right hand side (The camera moves closer to the subject by 1.9 mm after each exposure). There were 101 exposures in the series, and thus the total travel was 190mm. The vertical axis is MTF50, measured in cycles per picture height, assuming the entire sensor is used.
Now the other whole stops through f/11:
This is pretty spectacular performance, and compares favorably to the results on-axis.
Let’s look at focus shift in each raw plane:
Especially in the green plane, there is enough focus shift that you’ll want to focus at taking aperture. There is slightly more focus shift than in the on-axis graphs, indicating that field curvature changes very slightly with aperture setting. I don’t measure field curvature directly in these tests; in fact, I do all I can to calibrate it out.
For completeness, here are the focus shift graphs for a white balanced image:
Compare those to the corresponding on-axis graph:
The bottom curve has 51 samples per aperture, and the top one 101 samples. The bottom one also has f/16 and f/22 data.
There’s not much loss in sharpness at the corner. Good job, Sony!









Leave a Reply