Object-field methods for DOF management

This is a continuation of a report on new ways to look at depth of field. The series starts here:

A new way to look at depth of field

I will have more to say about the hyper-hyperfocal distance that I talked about yesterday, but I want to get started on something that I promised I’d get to back when I first started this series, object-field thinking, and its place (if any; you’ll have to be the judge of that) depth of field (DOF) management.

Before we get started, let me supply a little motivation. If you’ve been looking at the numbers in this series’ posts, I hope you’re getting the idea that, for critical work, under many field conditions, there isn’t as much DOF available as you’d like at diffraction levels that you’re happy with. If you’re in that predicament, it’s important to have a plan for what to make sharp and what to make not-so-sharp.

Object field thinking advertises itself as an approach that can bring clarity to the process.

So far, all our discussion of DOF and image sharpness has been in terms of what’s happening on the sensor and in the captured image as it wends its way through your chosen workflow. We haven’t had to have a name for that way of thinking, just like a fish doesn’t need a name for water; that’s all there was. But now we’ve got to call our old way of thinking something so that we can distinguish it from another approach. So we’ll call what we have been doing image-plane thinking.

Let’s imagine that we have a camera with a lens attached pointed at something that we wish to capture. The sensor is planar. The lens focuses (or not) light on the sensor from the world. The things in the world that comprise the photographic subject matter we’ll call objects, and they exist in three-dimensions, unlike the captured image. As a nod to the three dimensionality of our subject and the objects contained therein, we’ll call the part of the world that the camera can see the object field.

Object-field DOF thinking concerns itself with image sharpness and resolution of objects relative to their physical dimensions rather than relative to the size of the captured image. There’s a simple thought experiment that you can do to relate a known image plane sharpness metric to the corresponding object field one. Just imagine that the captured image at the sensor is instead projected upon the world with a perfect (no diffraction, no distortion) lens of the same focal length as the lens that’s taking the picture, and imagine how any softness in the image will be rendered as softness in the projection.

The way that object-field folk think of softness is in terms of circles of confusion (CoCs). I prefer MTF50. However, there’s nothing about the object-field method that ties it to any particular measure of sharpness or blurriness. I measure MTF50 in cycles per picture height (cy/ph) at the sensor plane, and in cycles per meter (cy/m) in the object field.

The thing that relates the MTF50s (or the CoCs, for that matter) in the image plane and the object field is the magnification of the camera’s lens, which, for objects sufficiently far away, is simply the focal length divided by the object distance (be sure to measure those two distances in the same units).

Examples; with a 55 mm lens, an object 55 meters away is magnified at the sensor plane by 1/000, or 0.001. If the resolution on the sensor measured in terms of MTF50 is 10 cycles/mm, then the resolution in the object field is 10 cycles/meter.  With a 400 mm lens and a subject 400 m away, the magnification and the MTF50’s would be the same.

If you know the resolution in the object field as an MTF50 number, you can invert that to get the size of the smallest detail that will be rendered with a 50% reduction in contrast. If the MTF50 is 10 cy/m, then one cycle would be 10 cm, so one dark line 5 cm wide and one light line of the same width would lose half its contrast.

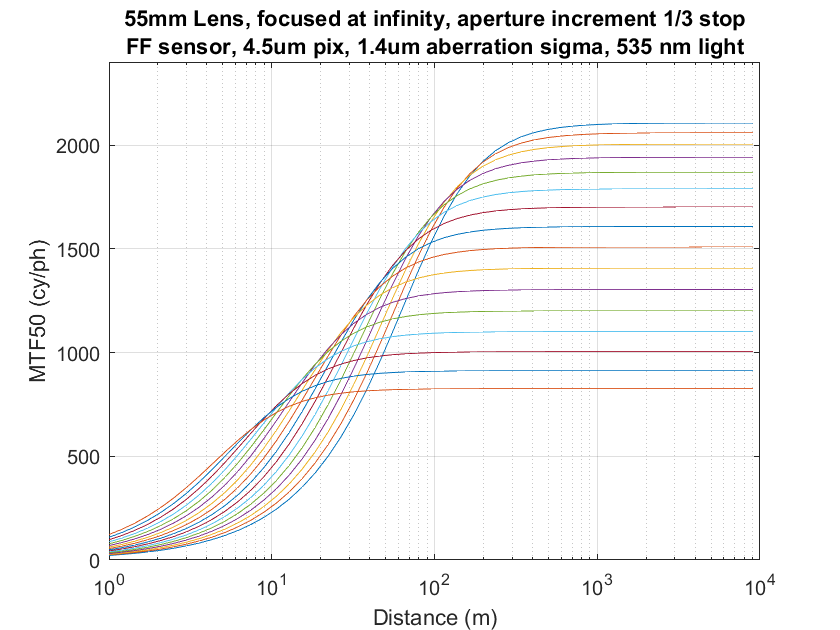
Remember this sensor plane set of curves from yesterday?

The vertical axis is the MTF50 in cycles per picture height you get when the lens is focused at infinity and the object is a a distance measured along the horizontal axis.

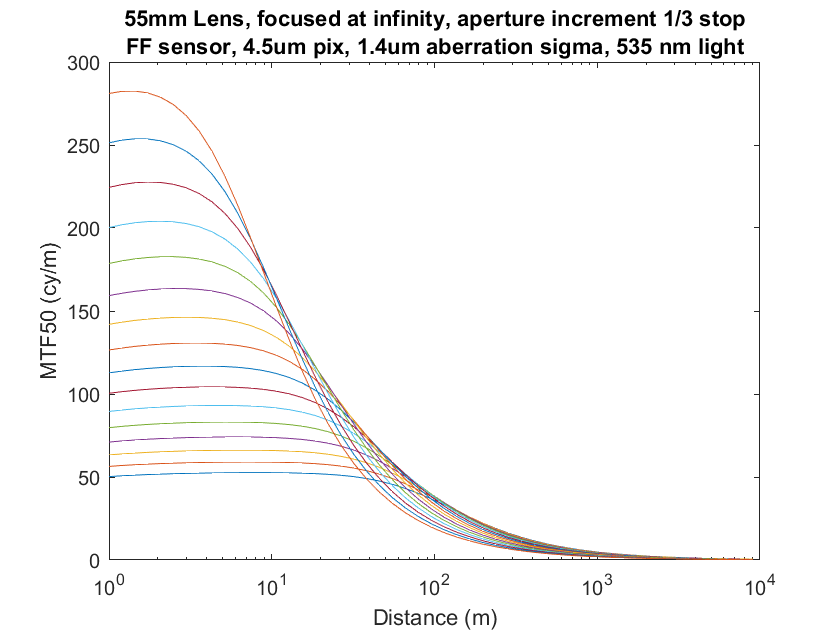
If we look at the MTF50 in the object field, it looks a little different:

The top curves are the narrower f-stops. You can see that, as the objects get farther and farther from the camera, they are less well resolved. No surprise there. What may surprise you, and what the object-fielders tout, is that the curves start out flat at the left side of the graph, meaning that the resolution measured at the object, doesn’t change with object distance if the lens is focused at infinity. However, this is not particularly useful for critical work, since the curves start falling before the best sharpness available at that f-stop is reached.

We can see what’s going on at great distances better if we make the vertical axis a log scale:

At great distances, diffraction is what differentiates the object-field resolution, just as it does in the image plane.

For a deep dive into object field methods  though,  with CoC rather than MTF50 as a measure of sharpness, have a  look here.