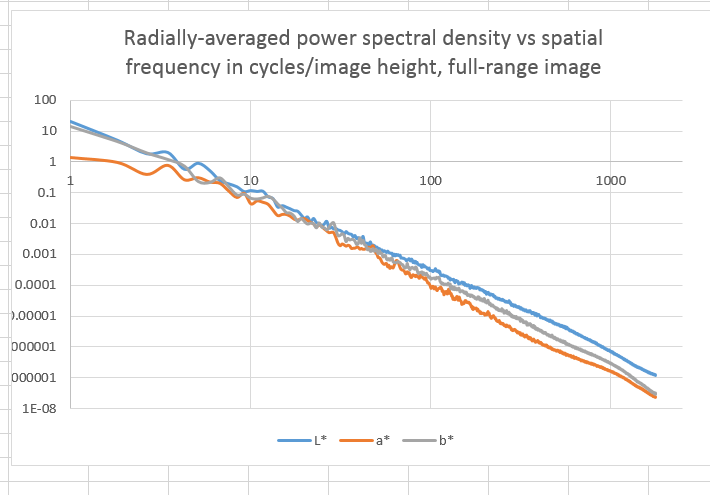
I ran the FFT analysis of yesterday’s post on a couple of more images. First, this old chestnut (thank you, Fuji):
Here’s what I got:
For the last three octaves of spatial frequency, the two chromaticity components are about the same distance below the luminance component.
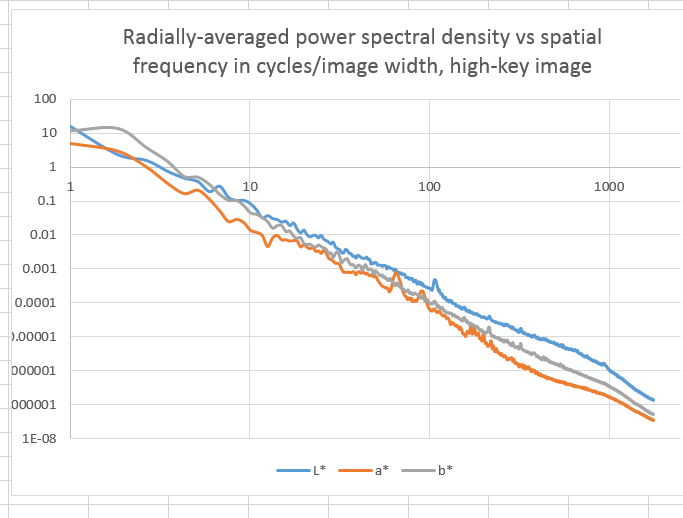
Then there’s this image (thank you again, Fuji):
Here’s the power spectral density analysis:
About the same as the so-called full-range image, with respect to the relationships between the luminance and the two chromaticity components over the upper three or four octaves.
I could do this for a whole bunch of images, but I’ve pretty much proven the point to myself. There’s nothing that makes the spectrum of the chromaticity components of a a real world want to fall off a cliff just before the luminance resolution limits of the image are reached.
And why should there be? If, say, the world had this property at normal photographic scales, we would take a picture from 40 feet away, and see small chromaticity changes at high spatial frequencies. Then, if we moved in to 20 feet, we’d see these same changes at half the spatial frequencies.
Now I admit that photographs of the world are not self-similar at all scales. If you back off, say, four or five light years and make a snap of the earth with an angle of view of 20 degrees, you’re going to see mostly black. If you get close, and I mean really close, so that your total image field is a few nanometers, you’re not going to see any color at all. In fact, you won’t be able to form an image with visible light.
But at normal photographic distances and angles of view, there’s no reason that I know of to think that, for a given angle of view, there’s some distance where the power spectral density at normal sensor resolutions drops precipitously.
Then why can we get away with sampling chromaticity components at lower rates than luminance? Stay tuned.


I had always thought that color television works not because of the nature of light but the nature of our rods and cones.
Ed, if you’re talking about the different bandwidths allocated to Y and the chromaticity components, UV or IQ, that’s not so much about he cones (the rods don’t come into play at the illumination levels common to TV viewing), but about the neural processing that follows, where a luminance and two color difference components are generated, and they differ in resolution. However, that processing stems from the different densities of rho, gamma, and beta cones, so in that sense, you’re right; it does go to the cones.
Jim
Jim,
Thanks for the explanation.
Doesn’t that imply that the A and B in LAB do not need to fall off faster than the L for us to be able get away with sampling A and B at lower rates than L (as in NTSC color TV)?
It certainly does, Ed.