This is the 17th post in a series of Nikon D850 tests. The series starts here.
Horshack has made an argument that if there’s bias to a PDAF system (as far as I know, CDAF systems don’t have biases), that can make the focus variations look larger when compared to a system where the average of many PDAF attempts is correct.
Here’s my version of his reasoning. All credit to him, and if there are errors, they are mine.
Consider a PDAF system with no bias:
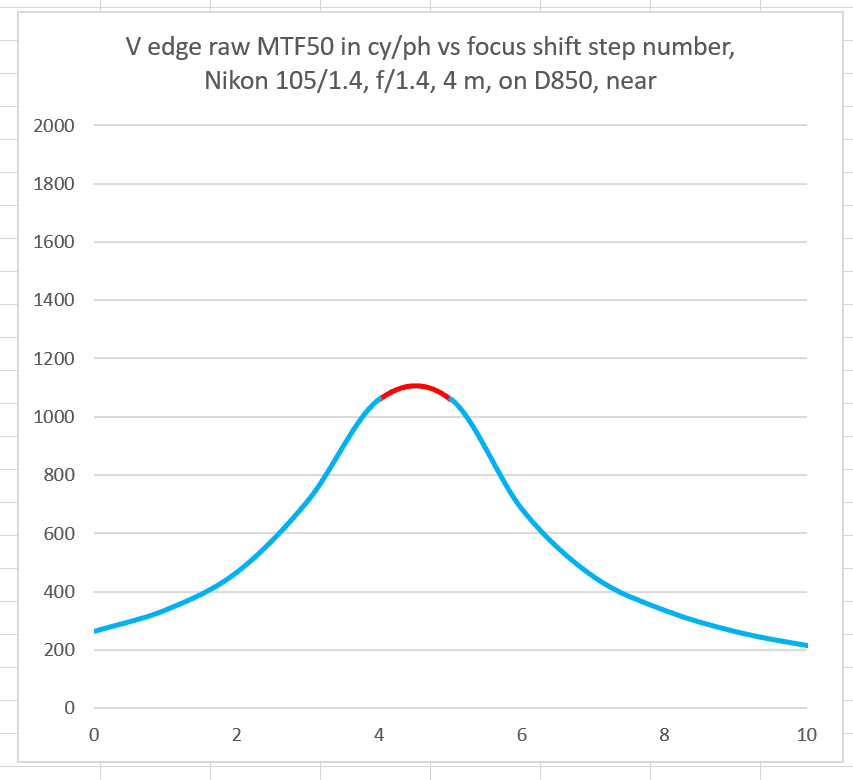
This is an actual raw-blue-channel MTF50 curve for the Nikon 58 mm f/1.4 wide open versus step number using the D850 Focus Shift Shooting feature with minimum step size. I’ve colored a part of the curve red. Think of a 1-step variation in focused distance, and see that the effect of the MTF50 numbers is not great.
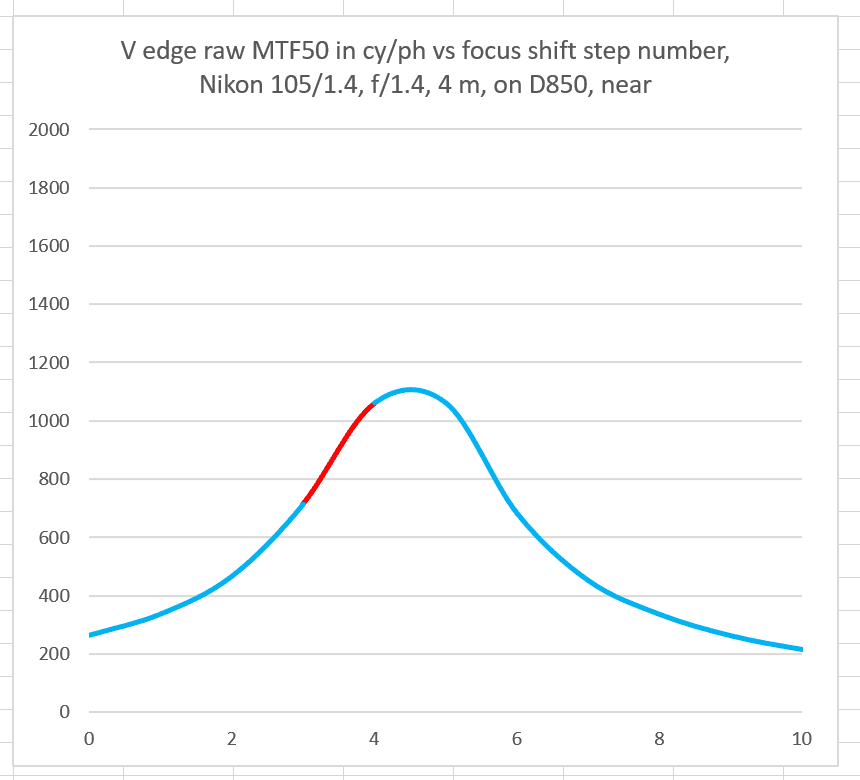
If there is the same one-step variation at a point that is offset from the peak, the variation in MTF50 is much greater.
The theory sounds good, but what about the practice?
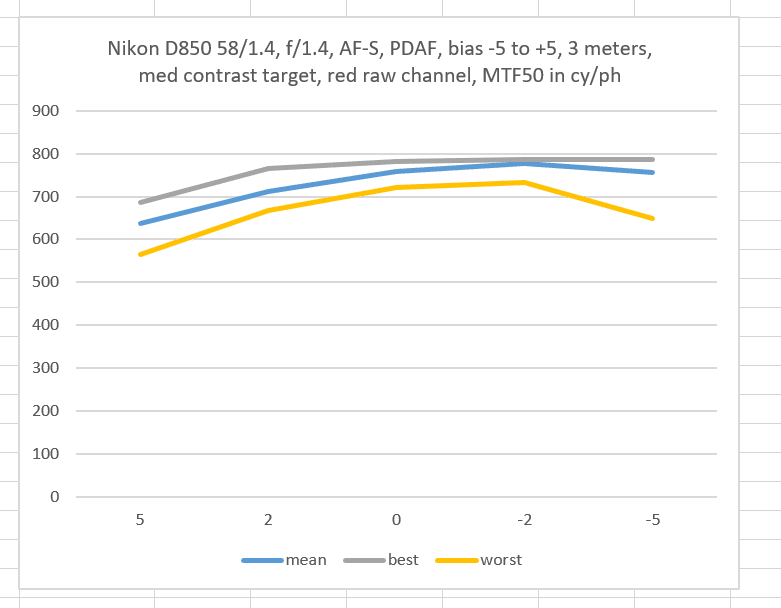
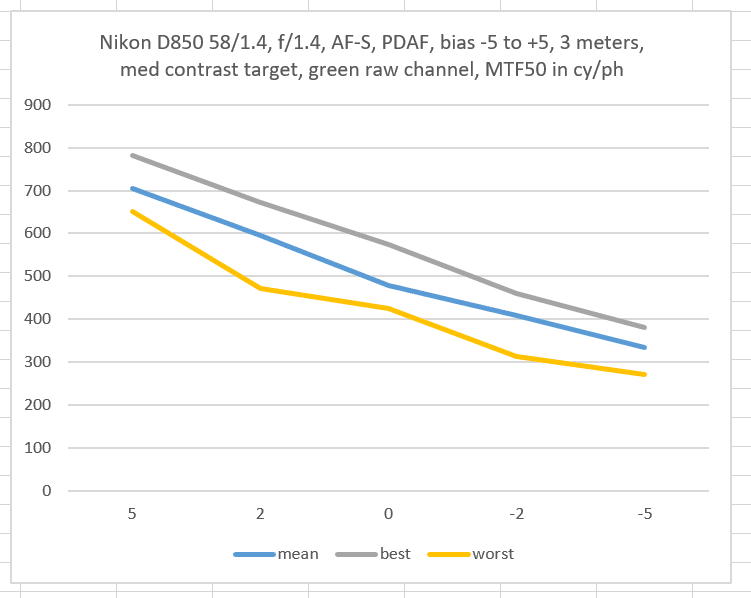
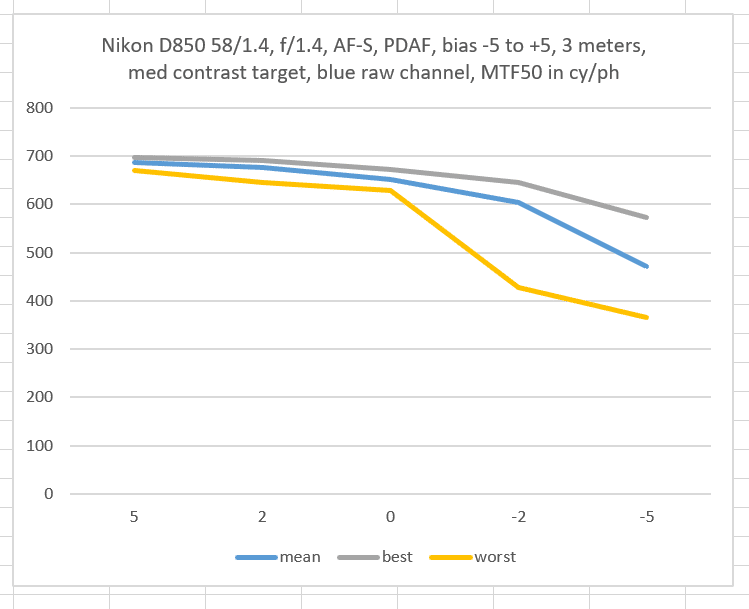
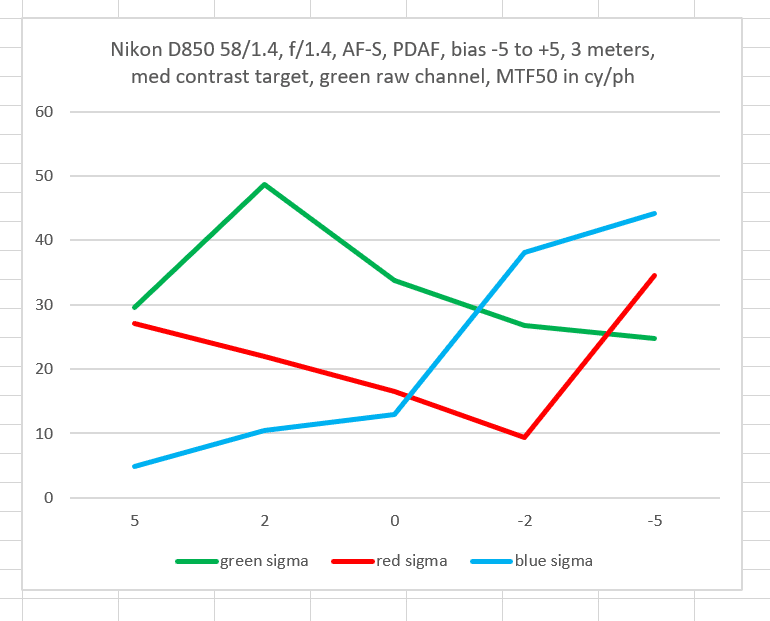
Consider these three plots from the immediately-previous post:
From the looks of the green curves, you’d expect that the standard deviation (sigma) would get larger as you proceeded from left to right.
But you’d be mistaken.
My conclusion is not that the theory is wrong, but that we need a lot more samples to prove it right. And no, I’m not gonna redo the tests with 1000 exposures at each bias. I also suspect that there are uncontrolled systematic biases in the tests I’m doing, probably related to how far defocused the lens is between each capture. I don’t know of a good way to control this that doesn’t involve a lot of work.
How about measuring the frequency with which the PDAF system chooses a particular focus distance?
Here is my thinking:
1. You have the MTF50 vs distance curve for your lens (obtained using the focusing rail).
2. You can take a measured MTF50 value, and use the inverse of the MTF50-vs-distance function to convert a measured MTF50 value into an approximate focus distance. The trouble is that the inverse is not a function, so you have to “rectify” the distance by using only the left half (relative to the peak) of the MTF50-vs-distance function’s inverse.
3. Now take a bunch of images using the standard PDAF procedure (i.e., reset lens to close/far focus in alternating steps), and use the inverse function from step 2 to produce a histogram of distances (rectified) that the camera settled on. (we can leave the AF-bracketing out of this for now)
This should directly reveal any bias in the PDAF system.
Anyhow, I think I can see Horshack’s line of reasoning with regards to the bias, but in practice we have to take into account that the sensitivity of the PDAF system will be greater on the slopes (vs. the peak) of the MTF50-vs-distance function, so I would not expect a closed-loop PDAF system to “settle” on the slope.
Part of this is likely the failure of MTF-50. Consider tracking the MTF at, say, half nyquist (~60lp/mm for the D850?) vs focus instead. The results will probably be a lot more predictable.
The SD of MTF-50 is not particularly meaningful either; the measurand changes between tests.
Thanks for doing this test Jim. I noticed the std. dev. increased markedly in the green channel between -5 and -2, owing to the “worst” sample, whereas the mean trend was constant through all the AFMA values. I’d be interested in seeing the underlying samples for the data. Could you post or email me the raw data for those? I’d love to see the 32 green-channel samples for each of the 5 AFMA values (-5, -2, 0, +2, +5), to get a better idea of the distribution.
Check your e-mail. I just sent you the whole spreadsheet. Hope that’s not TMI.