This is one in a series of posts on the Fujifilm GFX 100S. You should be able to find all the posts about that camera in the Category List on the right sidebar, below the Articles widget. There’s a drop-down menu there that you can use to get to all the posts in this series; just look for “GFX 100S”.
After I published this post, I got a bit of pushback from a reader. His contention was that DOF is defined by low-contrast portions of the image, and by measuring MTF50, I was looking at high-contrast areas. I don’t buy the premise, but I thought it worthwhile to take a look at the ability of MTF50 to predict the behavior of lower-contrast MTFxx’s, like MTF20 or MTF10.
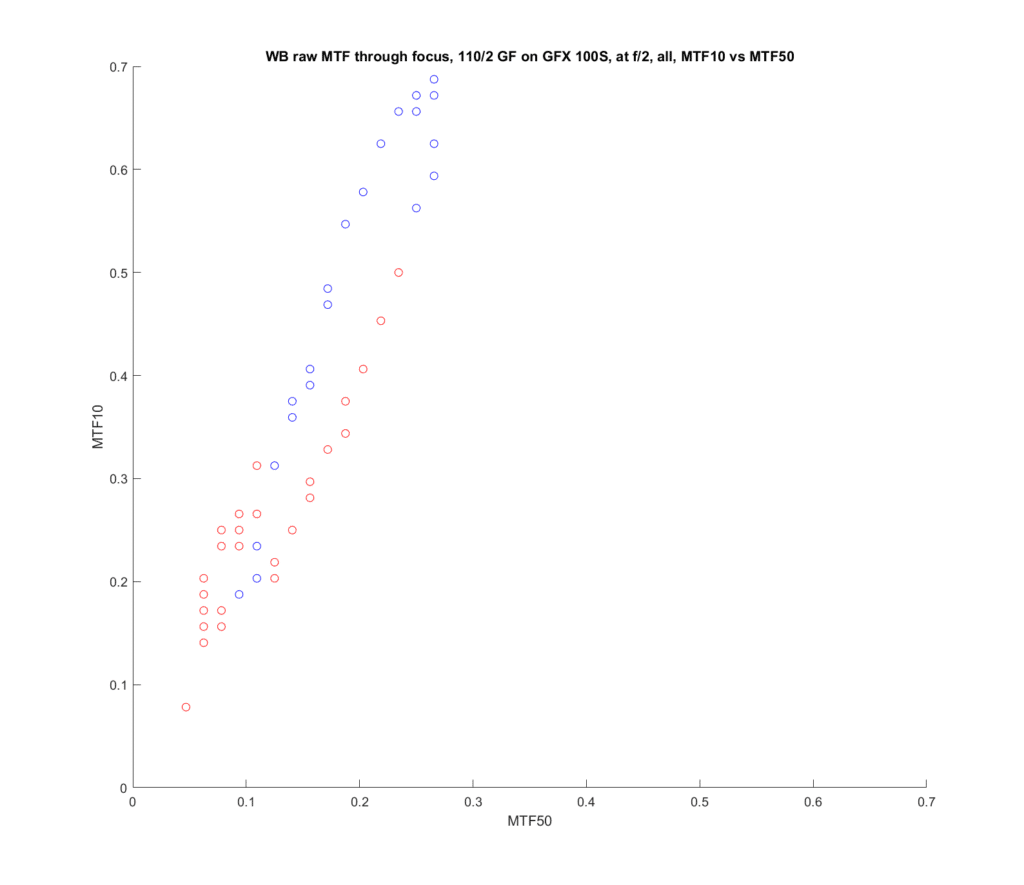
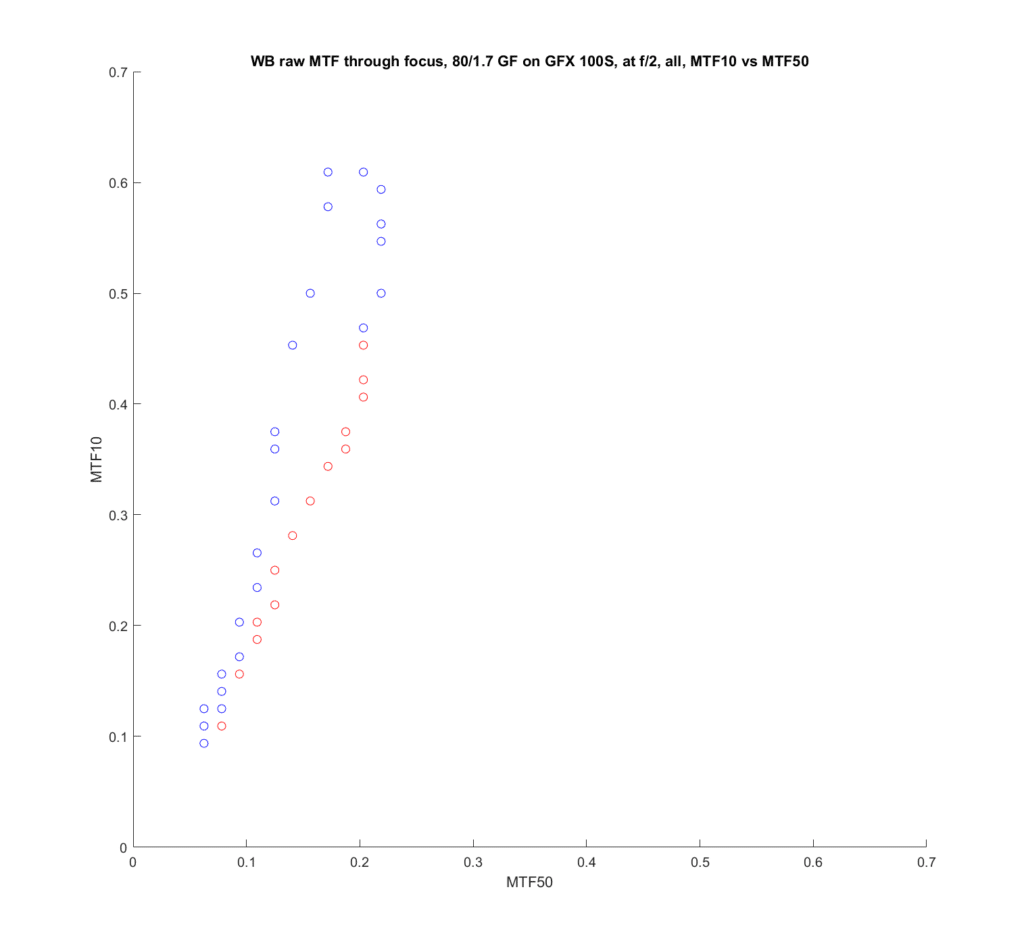
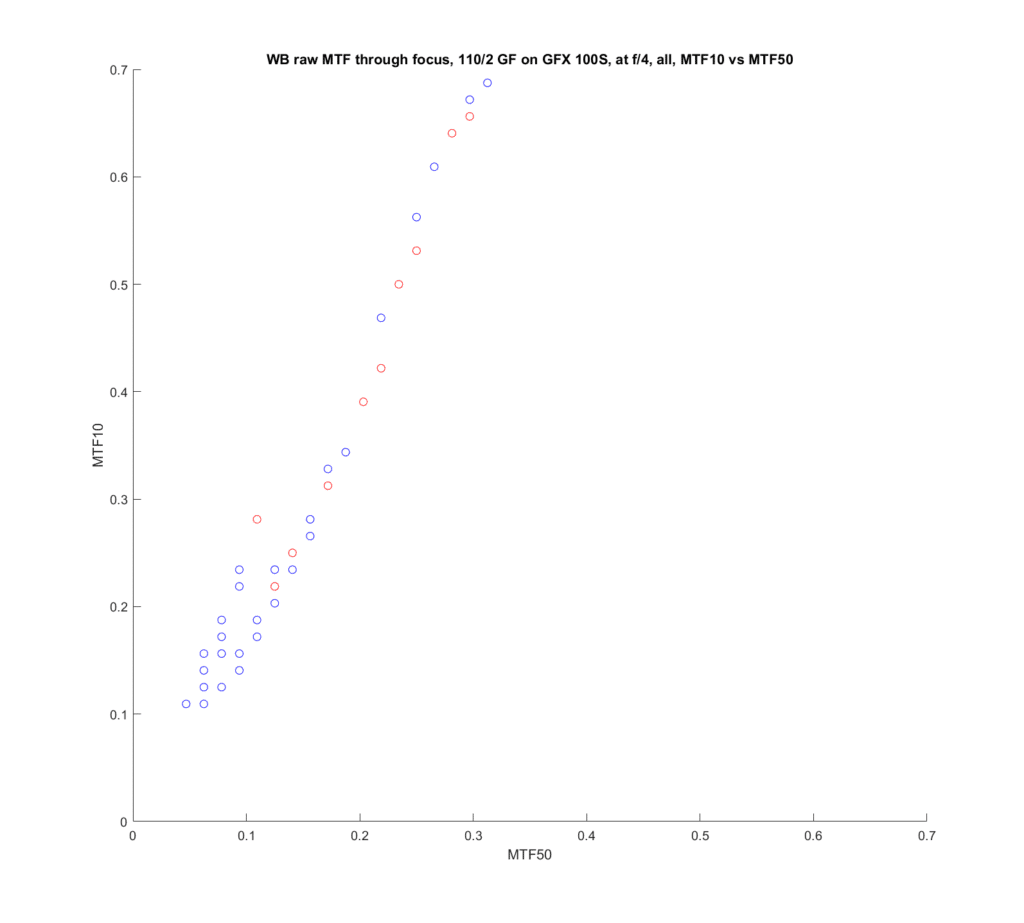
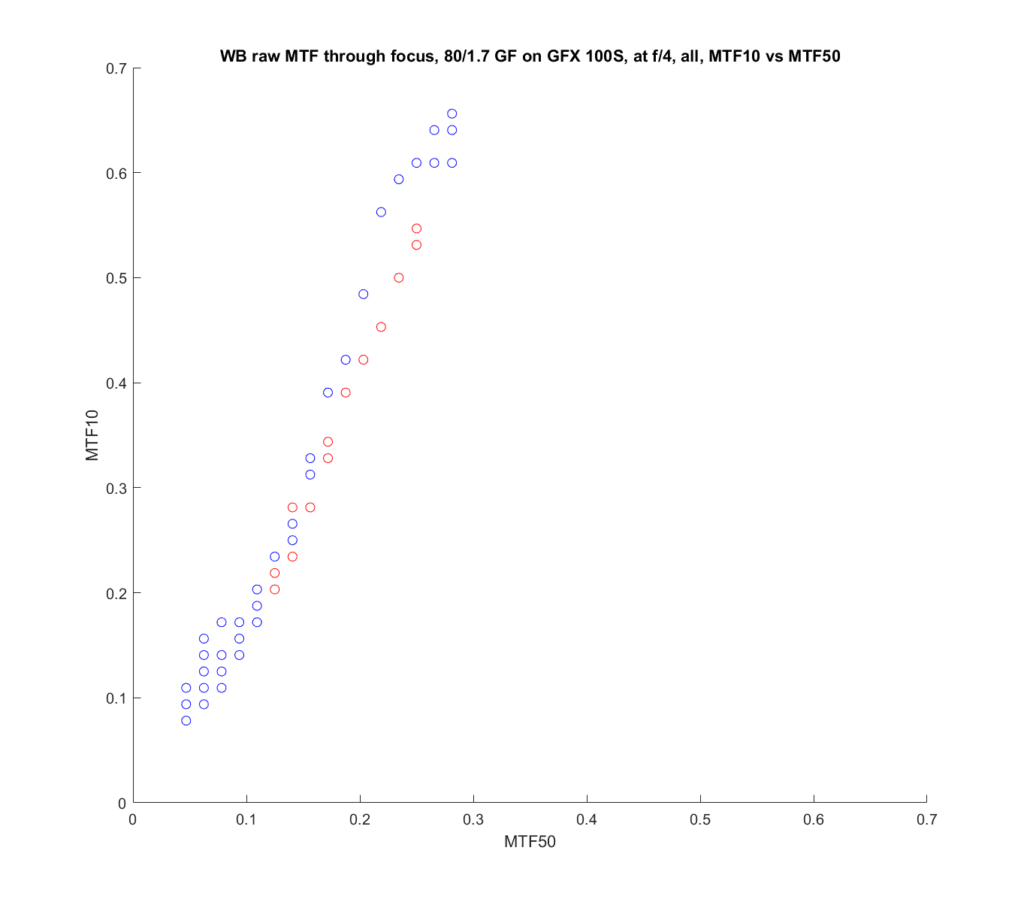
I took the through-focus tests that I did of the Fujifilm 80 mm f/1.7 GF and the 110 mm f/2 GF lenses on the GFX 100S and created scatter plots of MTF10 versus MTF50 for all the images. I didn’t do any fancy curve-fitting, so the data jumps around due to the vicissitudes of the GFX focus bracketing system, but it’s enough to get the idea. There is also no interpolation, so both sets of data are rather coarsely quantized. At wide apertures, the 110 and the 80 both have different MTF curves when they are front-focused and when they are back-focused. In order to make that easier to sort out, I colored the front-focused points red and the back-focused points blue. The coloring isn’t perfect, but, again, it’s good enough to get the idea.
Without further ado, here are the plots, first at f/2:
MTF50, in cycles per pixel, is plotted on the x axis, and MTF10, also in cycles per pixel, is on the y axis.
There is strong correlation of MTF10 to MTF 50, but, for the saem MTF50 values, the MTF10 values are higher when the lens is back-focused than when it is front-focused. This means that there is relatively more low-contrast detail when the lens is back-focused. Even though the 110/2 and the 80/1.7 are quite different designs, with the 110 being better corrected, the effect appears for both lenses. The effect occurs most strongly at high MTF50. When the MTF 50 is down around 0.15 cycles per pixel, it hardly exists at all.
You should take the MTF10 numbers above 0.5 with a whole box of salt. Half a cycle per pixel is the Nyquist frequency, and any information captured above that frequency will be improperly reconstructed in the photograph.
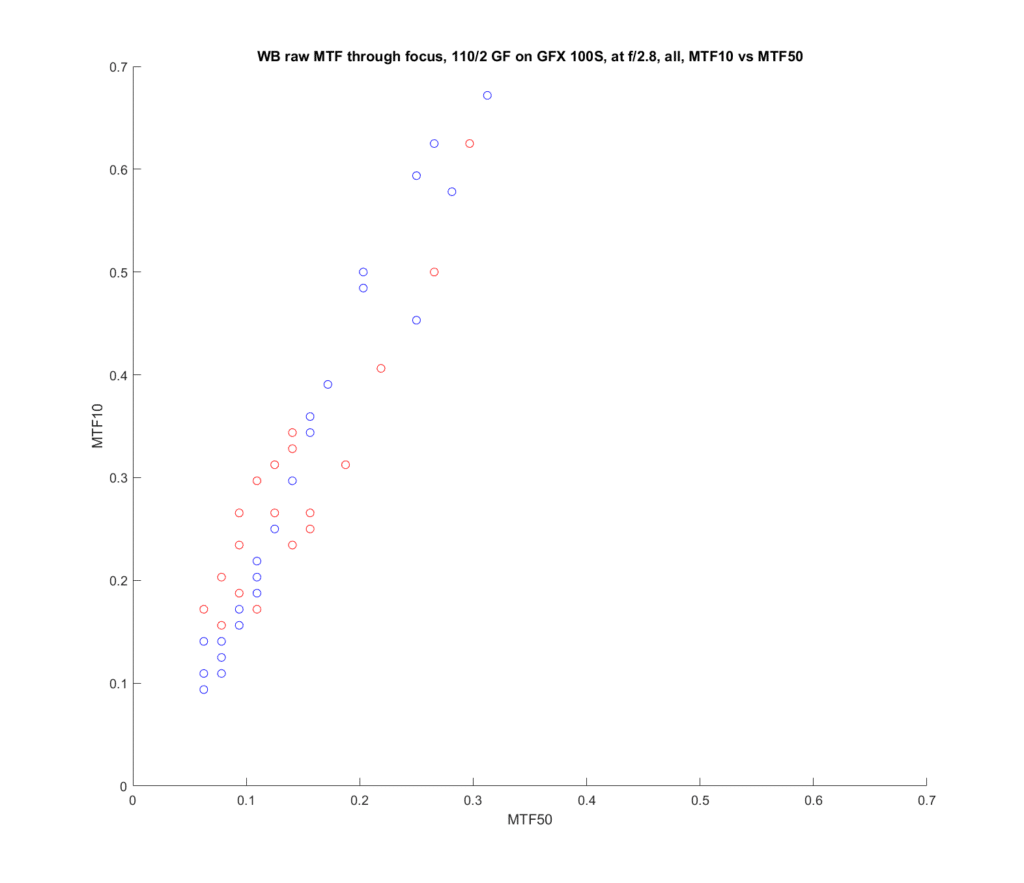
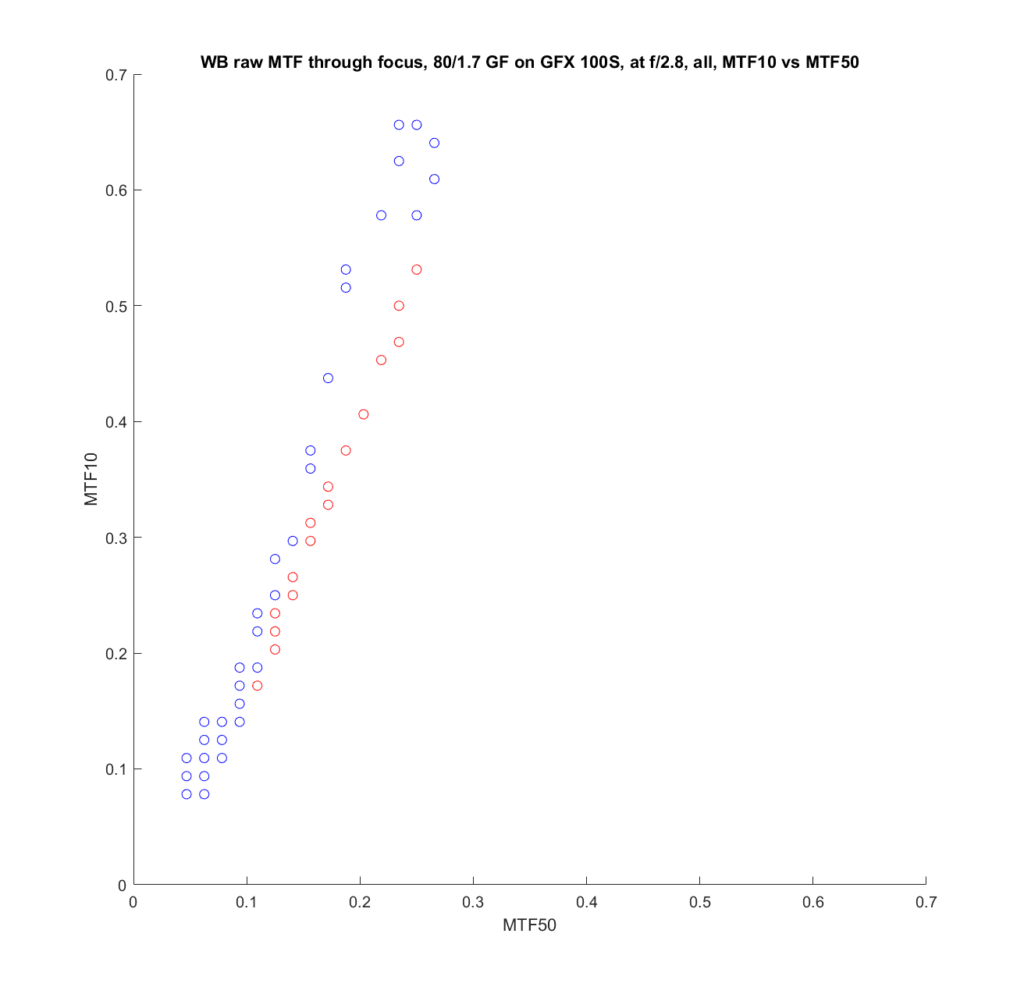
Stopping down to f/2.8:
In both cases, the effect is reduced, and hardly exists at MTF50s below 0.2 cycles per pixel.
At f/4:
The effect is almost gone.
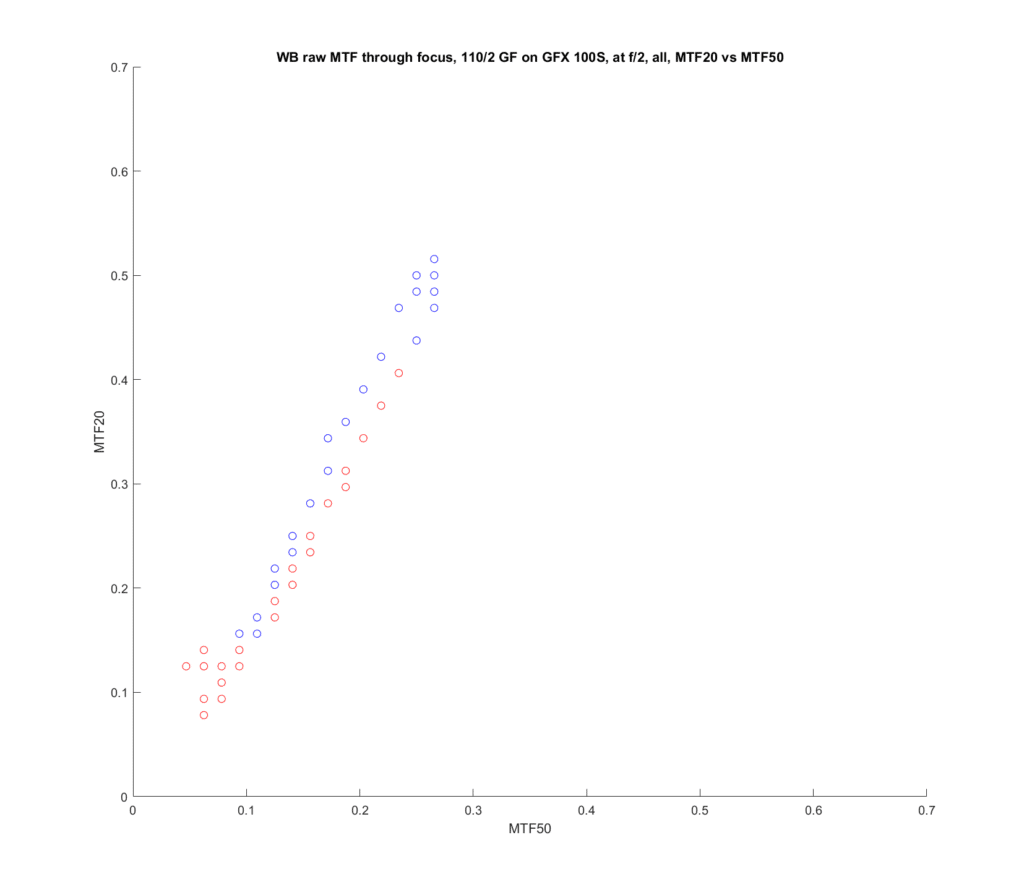
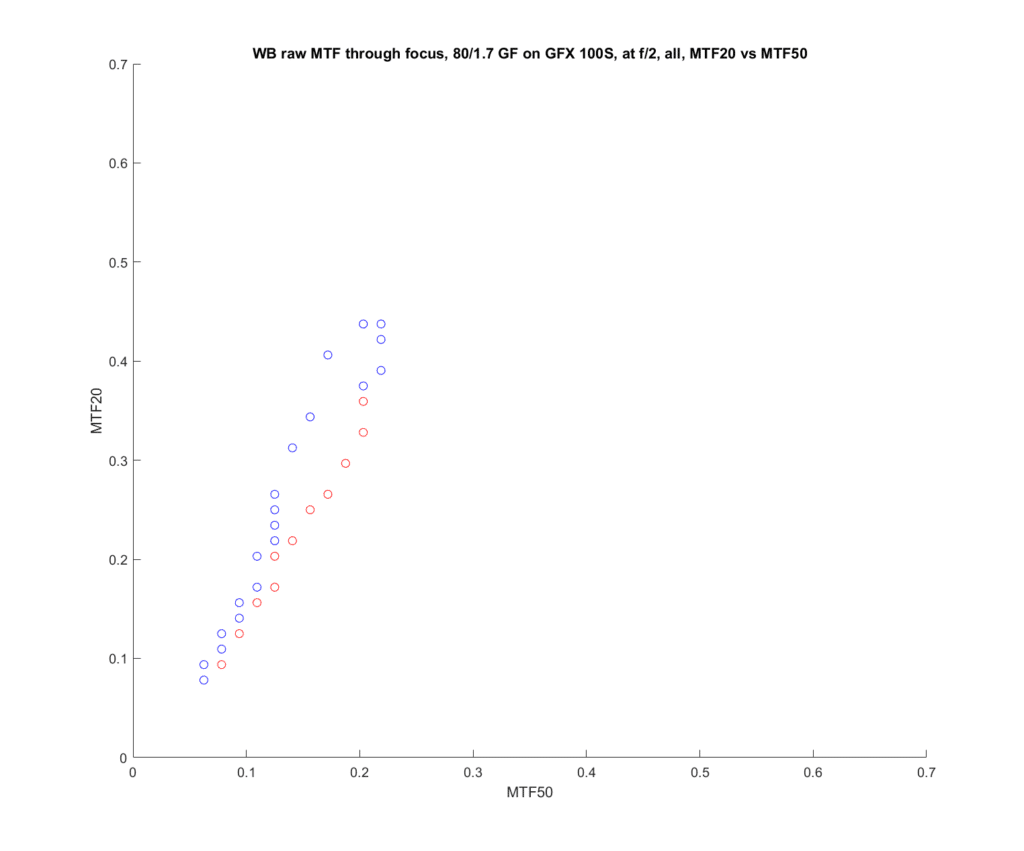
I plotted similar curves for MTF20 vs MTF 50, and they looked roughly the same, but the asymmetry around the correct focus was smaller, especially with the 110/2.
Here are the f/2 plots:
I think I’ll continue to use MTF50 for these tests. However, I’m working on ways to present the entire MTF curve for these through focus tests.
Here’s a teaser:
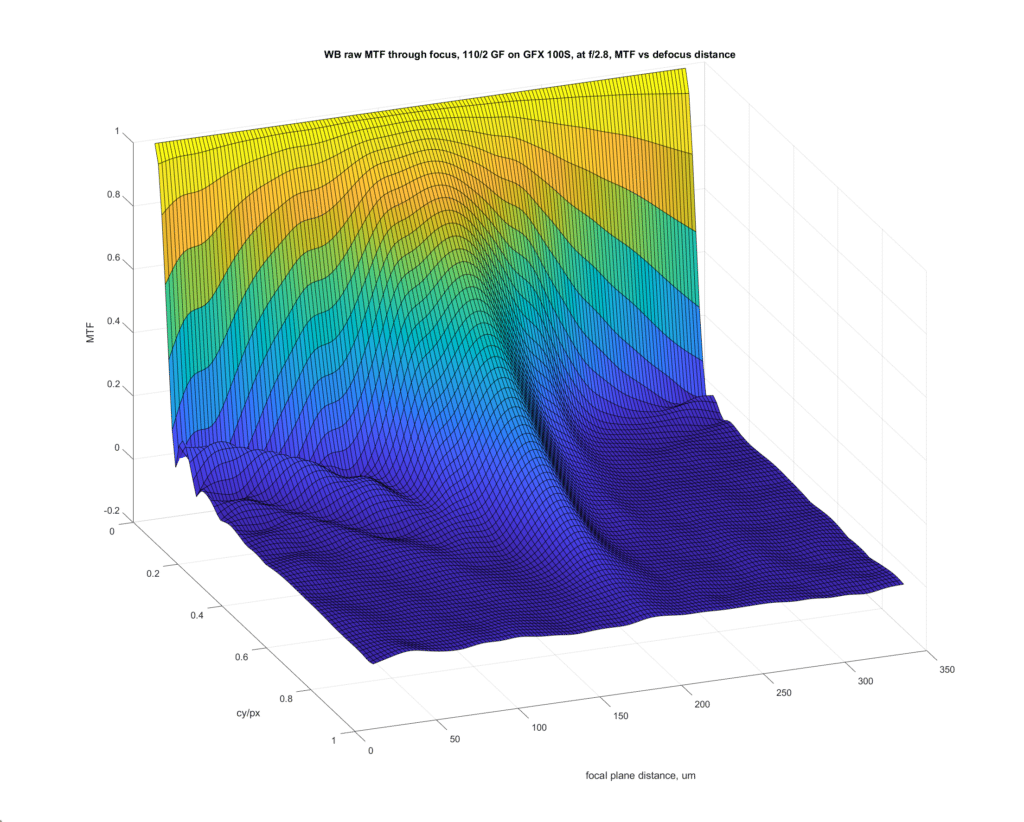
I seriously doubt anyone could tell the difference between the DOF characteristics of the real image and one approximated using a linear fit between the MTF10 and MTF50 shown above, assuming LOCA and everything else were kept the same. I suspect that the relationship to higher contrast levels would be even better. For defocus at least, I am convinced that MTF50 provides a good scalar metric for most of the MTF.
It would be fun to see the full MTF curve vs defocus. Time to pull out a 3D plot? Color scale a 2D image of the data?
Working on it. It looks pretty ugly with the raw data. I’ll see if I can apply the same smoothing algorithm I used before.
It would be good for you to replicate figure 34 from my thesis, and fig 37 if you try to do any model fitting. https://www.retrorefractions.com/pdf/bdd_ug_thesis_10.pdf
Thanks, Brandon. I was thinking either something like that, a 3D surface, or a contour plot. But I’ve got to smooth the data first.