A couple of days ago, a poster on the DPR MF board made a remarkable claim in response to speculation about a 100 MP X-series Hasselblad.
One word, diffraction. The X1DII and X1D doesn’t have, none or perhaps very little that I’ve noticed anyway.
As you might expect, I challenged that assertion:
Lenses suffer from diffraction. Sensors don’t, at least under normal photographic conditions.
He came back with:
Actually lens diffraction is affected by pixel size, not sensor size. I looked it up :-).
“Diffraction is related to pixel size, not sensor size. The smaller the pixels the sooner diffraction effects will be noticed. Smaller sensors tend to have smaller pixels is all. A 50mp sensor will be effected [sic] at larger apertures than a 10mp camera of the same sensor dimensions.”
There are things that are mixed up in that, and things that are just flat wrong.
The first conflation is the lack of distinction between the effects of diffraction and the visibility of those effects. The size of the Airy disk is not a function of sensor size, pixel pitch, or pixel aperture. The size of the Airy disk on the sensor is a function of wavelength and f-stop. That’s all. The size of the Airy disk on the print is a function of both those, plus the ratio of sensor size to print size.
The second confusion is between the size of the pixel aperture and the number of pixels on the sensor. Unless we’re talking about multishot regimes like pixel-shift, the largest effective pixel aperture we usually see is close to 100% of a square with sides equal to the pixel pitch. But we used to see apertures that were much smaller than that, and in some cameras, notably the Fujifilm GFX 50S and GFX 50 R, we still do.
There is also no clear distinction between the size of the diffraction disk on the sensor, the size of that disk as projected to the final print, and the size of the blur pattern created by the diffraction and the finite pixel aperture.
I’ve done a lot of work on diffraction before, and that work calculated the effects of the diffraction, pixel aperture, and defocus on blur circle size. Sometimes I used fairly rigorous simulations that took into account the phase of the light, and sometimes I used more approximate methods like the ones I’ll be using in this post. I’ll draw upon that work to tackle the issue of how pixel aperture and diffraction interact directly here.
I made some assumptions:
- 555 nanometer incoherent green light
- No lens aberrations
- Pixel aperture is circular, with 100% sensitivity within its diameter
- No Bayer color filter array. The way the effects of that array interact with all of the demosaicing algorithms is too complicated for me to model.
- I’m ignoring phase effects.
- Circular lens aperture
To approximate the size of the combined blur circle I to the square root of the sum of the squares of the pixel aperture and the diameter of a circle that included 70% of the energy of the diffraction disk. The more conventional approach would have been to take as the diameter of the diffraction disk the distance across the disk between the first zeros, but I have found in the past that that overstates the contribution of diffraction.
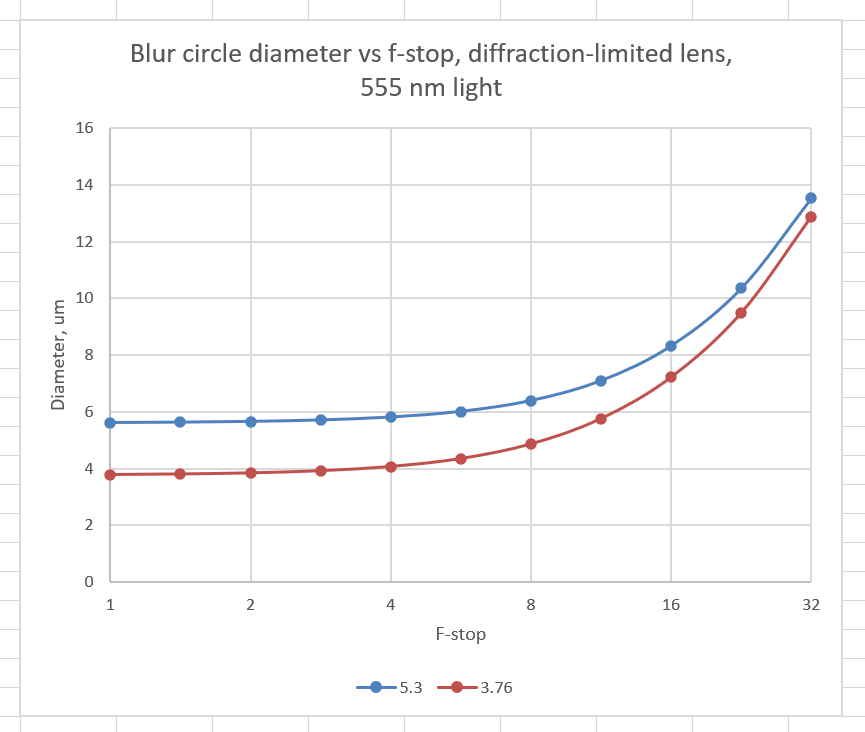
Here’s a plot for two pixel aperture diameters, 5.3 um and 3.76 um.
Excellent lenses often lose significant sharpness to diffraction on axis by f/4 or f/5.6. Most decent lenses are getting to be diffraction-limited by about f/11. On the left hand side of the graph, there is little diffraction and the combined blur circle is determined by the pixel aperture. By the time you get to the far right, the diameter of the combined blur circle is mostly the result of diffraction. I ran the calculations out to f/90, where the curves are almost right on top of each other, but I’m not showing it because the scale required makes it hard to see the differences at apertures that you’d be more likely to use.
- The format of the sensor — MFT, APS-C, full frame, 33×44 mm, or whatever you want — makes no difference.
- The focal length of the lens makes no difference.
- The subject distance makes no difference, except as it affects effective aperture
The pixel pitch makes no difference, either, at least explicitly. It is true that finer pitches usually go along with smaller pixel apertures, so inpractice they are related. However, the pixel apertures on both the Fujifilm GFX 50x and the GFX 100 are both about 3.76 um in diameter, even though the pixel pitch of the GFX 100 is 3.76 um and that of the GFX 50x is about 5.3 um. It is possible that the Hasselblad X1D has more conventional microlenses than the GFX 50x, and so the 5.3 um line might be more appropriate for the X1D.
The question of the visibility of the diffraction has two answers, depending on how you ask the question. If you ask the question “when does the diffraction dominate the sharpness of a well-focused subject”, then the size of the pixel aperture is important (not the pixel pitch: that affects aliasing). When a lens is stopped down to f/11, f/16/ or f/22 and focused accurately, it is likely that the lens aberrations are unimportant compared to the blur induced by the Airy disk. The size of the blur at the sensor is, neglecting phase effects, equal to the size of the convolution of the effective pixel aperture and the projected Airy disk. If the Airy disk is much larger than the pixel aperture, then virtually all the blur you see in the image will be due to the diffraction.
The graph above is a fairly good way to approach the above question. When the curves get close together, diffraction is dominating. When they are far apart, the pixel aperture blur is dominating.
The other way to phrase the question is “when does the diffraction begin to affect the sharpness of a well-focused subject”. If you phrase it that way, that happens when the size of the Airy disk becomes non-negligible compared to other blur sources. There are two main other blur sources to consider: the lens aberrations and the pixel aperture. The point at which the reduction in blur caused by stopping down the lens are reducing its aberrations stops producing sharper images because that same stopping down introduces more diffraction is dependent on the lens, and not on the pixel aperture.
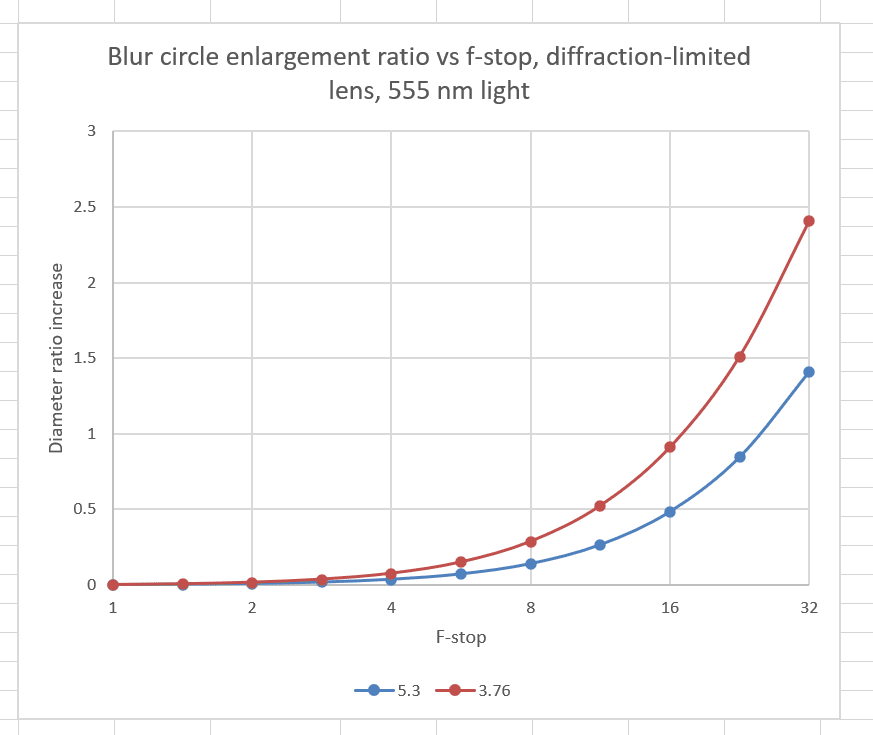
The next graph is an attempt to deal with the second question.
What is plotted is the ratio of the combined blur circle diameter to that of the no-diffraction case less one. The horizontal line that crosses the y-axis at 0.5 means that diffraction has made the blur circle grow by 50%. That point occurs at f/11 for the sensor with pixel aperture diameter of 3.76, and at f/16 for the sensor with 5.3 um pixel aperture. So all else equal the effects of diffraction are more visible on the sensor with the smaller pixel aperture.
If the X1D has a pixel aperture of 5.3 um, you’re going to see pronounced diffraction effects at f/16. I can’t imagine that he X1D has a pixel aperture larger than 5.3 um, so that’s the best case for an assertion that you don’t have to worry about diffraction is your using an X1D. If the X1D pixel aperture is more like the GFX 50S and GFX 50R, then you’ll see the same relative amount of degradation at f/11.
But the bottom line for the X1D diffraction claim that led off this post is that increasing the resolution of the sensor with the same ratio of pitch to pixel aperture won’t make the effects of diffraction any worse in the capture at the same print size. In fact, it will make is better. Look at the top graph above. Consider the two curves as applying to two cameras with 5.3 and 3.76 um pitches, with pixel apertures equal to the pitch. Note that the combined blur circles are always smaller for the finer-pitch sensor, even though the differences are less significant at narrower apertures.
> “Excellent lenses are close to diffraction-limited on axis by f/4 or f/5.6.”
Com’on! Which measure of ”close” do you use here? I would say “comparable” — but IMO “close” is too strong a word.
At f/4, the MTF of diffraction is 86% at 50 lp/mm and 550 nm. Which lens performs close to this?! At ƒ/5.6 indeed, the best lenses get somewhat close (the required MTF is 80%).
> “… the size of the Airy disk …”
My usual gripe with these words: this size was a good measure of diffraction in 19th century, but not now. A SIGNIFICANT part of effects of diffraction can be eliminated by DSP. Therefore in context of digital acquisition, the half-period of the “diffraction cut-off-frequency” is way more relevant as the measure of diffraction. It measures what CANNOT be fixed by postprocessing — and IIRC it is almost 2.5 times smaller!
I changed the wording about f/4 and f/5.6.
WRT to the Airy disk size, I am using the EED70 diameter, which is 0.7/1.22 of the first zero diameter.
http://spider.ipac.caltech.edu/staff/fmasci/home/astro_refs/PSFtheory.pdf
This reference is related to *photometry.* In *photography* (with a decent RAW converter) what is relevant is the metrics related to DSP. Hence they should be based on MTF.
At EED70, MTF is almost 19%, which is still “very good”. In my experience, the practically interesting cut-offs are about 5%. Moreover, the relevant spacial frequency is so close to the “theoretical cut-off” frequency (MTF=0 ) that one can forget about all “arbitrary decisions” and use the “unambiguous” MTF=0 as the representative cut-off.
[But I think I ranted about this many times already, so feel free to ignore this particular diatribe! ;-)]
For example, the 85/1.4 Otus passes the Marechal criteria under photopic light at F/4.
Do not remember seeing this, can you provide the reference? (I remember something from your thesis, but it was some Canon IIRC…)
And cannot find the corresponding MTF⸣s on Roger’s site (although I remember seeing it before). Do you know the corresponding MTF (hmm, anyway it should be easy to calculate…).
I did my calculations, and reconsidered:
• the Marechal criterion essentially describes the MTF at very LOW spacial frequencies.
• While the MTF I discussed above (at the 0.7 of the cut-off frequency) correlates well with the (averaged) phase error in the ring-like zone with radius ∼0.7 of the aperture. This may be quite different from the phase error averaged over the whole aperture.
CONCLUSION: when comparing MTF of diffraction to the MTF of the sensel, Marechal’s criterion is not VERY relevant. (Still, such an achievement is amazing!)
I’m not sure where you’re going… the ask was about how can you claim diffraction limited, or a just noticeable difference to that.
The Maréchal criteria is the most typical way to specify diffraction limited or not. The Otus 85/1.4 passes that test at F/4.
It is related through Strehl to the integral of the MTF division by the diffraction limited MTF. All spatial frequencies are relevant.
The data I derived that from is not public. It was done by performing more classical PSF based phase retrieval, using highly oversampled imagery from the camera in Trioptics’ machine.
There is not a general clean connection between certain spatial frequency ranges and zones of the pupil. Perhaps with only rotationally symmetric wavefront error or some other restricted case, but not in general.
What is the definition of pixel aperture? I did a Google search but did not find a link for this term. Thanks.
The dimensions and sensitivity of the part of the pixel on the sensor that responds to light.
Hi Jim,
thanks for the explanation and for the comprehensive post as usual. Hope everything is ok and to see more blog posts in the future.
Actually I though about this topic when testing Pixel shift on the GFX100 (btw did you try that? Looking forward to seeing a post with your thoughts). I tested the results of pixel shift vs normal image at f/11 and was disappointed with the results: almost no visual improvement at all. Then it came to me that there could be a “diffraction related issue” and I tried again at f/5.6: this time it was much better.
Is this related to the explanations you wrote above? Something like considering pixel shift as reducing the actual pixel pitch/pixel aperture?
By the way, I am not really satisfied with pixel shift results from the GFX100 anyway (my personal empirical feeling is that there is a HW or SW imperfection), and wanted to try with an A7RIV to compare results (shooting the GFX100 in crop mode of course). That’s also why I would be eager to see your test.
Thanks in advance for any input!
Best Regards,
Michele Barana
I tested pixel shift on the Sony cameras, including the a7RIV, which has the same pixel pitch as the GFX 100. I think it would be useful in the studio, especially for fabric and art reproduction, but the artifacts occur too often for me to want to use it outdoors. I’ve never used it for anything other than testing. Because I view the feature as having such limited utility, I never tested it with the GFX 100. It will probably work about as well as it does on the a7RIV.
Thanks Jim, I plan to borrow an A7RIV and will do some comparisons.
In case there are interesting results I will add to this post.
Michele
I find it interesting that you would devote an entire article or study based on my casual comments about diffraction. In one way I’m honored that you would spend so much time on my passing comments yet I’m humbled by your action. My point was and still is that there is more than one side of opinions on diffraction.
I mis-worded a comment or two. “Actually lens diffraction is affected by pixel size, not sensor size. I looked it up :-).” I should have included or written “the effects of diffraction is apparent sooner with smaller pixel sizes”.
I agree with most if not all of what you’ve written below.
“What is plotted is the ratio of the combined blur circle diameter to that of the no-diffraction case less one. The horizontal line that crosses the y-axis at 0.5 means that diffraction has made the blur circle grow by 50%. That point occurs at f/11 for the sensor with pixel aperture diameter of 3.76, and at f/16 for the sensor with 5.3 um pixel aperture. So all else equal the effects of diffraction are more visible on the sensor with the smaller pixel aperture.
If the X1D has a pixel aperture of 5.3 um, you’re going to see pronounced diffraction effects at f/16. I can’t imagine that he X1D has a pixel aperture larger than 5.3 um, so that’s the best case for an assertion that you don’t have to worry about diffraction is your using an X1D. If the X1D pixel aperture is more like the GFX 50S and GFX 50R, then you’ll see the same relative amount of degradation at f/11.
But the bottom line for the X1D diffraction claim that led off this post is that increasing the resolution of the sensor with the same ratio of pitch to pixel aperture won’t make the effects of diffraction any worse in the capture at the same print size. In fact, it will make is better. Look at the top graph above. Consider the two curves as applying to two cameras with 5.3 and 3.76 um pitches, with pixel apertures equal to the pitch. Note that the combined blur circles are always smaller for the finer-pitch sensor, even though the differences are less significant at narrower apertures.”
While as far as I know it is true that better MTF from a lens and a sensor with more MP’s will offset much of this loss from diffraction that actually results with more resolution.
The caveat and questions that I ask are what about the contrast loss and the color shifting caused by diffraction? Color shifting being caused by from what I’ve read are the photons being scattered and sent to different wavelengths which in many cases must change to maintain the constancy of the frequency.
I know, probably a controversial subject depending on who says what. And I’m sure with that my zero engineering and science backgrounds that I got a few things mis-construed or just wrong. I am in the camp that says that there is more than just resolution loss that is experienced with diffraction. Feel free to comment otherwise, I’m all ears.
“what about the contrast loss and the color shifting caused by diffraction?”
Contrast loss is due to diffraction blurring the undiffracted image, the effect of which is what MTF measures quantitatively at various spatial frequencies. In photography diffraction is typically controlled by the f/stop and varying it may result in other image changes like vignetting etc. which may be perceived as a change in contrast.
As for color, shifting is probably the wrong word. Diffraction’s blur function from a circular aperture looks the same at all wavelengths but its scale depends on the effective f-number (N) multiplied by the wavelength (lambda) of the light (e.g. the diameter of the Airy disk is about 2.44*lambda*N). So light of longer wavelengths would be blurred more than light of shorter ones. This, combined with typically stronger effects from lens aberrations like SA and CA can create color artifacts, Jim has some good posts in here about those.
If you want to suss out some of your thoughts further, start a thread on the PST forum at DPR, you’ll get good feedback.
That is only true if qualified so that the baseline is the pixel pitch in each case. It it not true at the same print size. I submit that, if we’re making photographs, same print — or display, to generalize a bit — size is the appropriate approach.
Somehow I’m not getting my point across to you.
And my point, which I made in the DPR thread and which you disagreed with there, is that this is not a matter of opinion. It is a matter of fact. Diffraction is well understood, and has been for a long time. If the propositions are worded precisely and clearly (which I’ve tried to do, but I think you have not), disagreements such as this one can only result if one or both of the parties to the disagreement are wrong.
It was more than casual comments. It was a debate. And I wouldn’t have written a blog post if you were the only person misunderstanding how diffraction and sampling aperture interrelate. But you’re not. There are many others with the same set of misconceptions. Hence the desire to use our discussion as a springboard to a post that may get a wider audience.
Diffraction does not change the photon frequencies. Different wavelengths are by scattered different amounts. The size of the Airy disk changes in proportion to the wavelength. I have no idea what you mean by this:
.
The link is one of many I’ve read, perhaps they’re wrong. I find the last comment interesting as it mentions wavelengths and color shifts.
https://physics.stackexchange.com/questions/321395/diffraction-of-light-and-color-change#:~:text=Diffraction%20occurs%20when%20a%20wave,wave%20are%20changed%20by%20diffraction.&text=Again%2C%20the%20only%20change%20is,colour%20of%20light%20never%20changes.
I appreciate all of the comments and responses, it is certainly a learning process, well worth the read.
The last comment actually corrects the penultimate comment, which talked about wavelength changes. What’s important is the photon energy. In any case, the medium both before and after the lens is air, so that situation doesn’t apply.
Jim
Then there is also a blooming effects in the sensor. New sensors have smaller pixels but the blooming effects are possibly smaller as well thanks to new developments in sensor techniques like deep trenches around the pixels.
http://image-sensors-world.blogspot.com/2021/02/albert-theuwissen-delivers-keynote-at.html
Modify message
I haven’t noticed that blooming is significant in today’s FF and MF cameras. It was different in the CCD era, though.
Hy!
Great post as usual! Just one question: Nikon claims they are using some kind of anti-diffraction algorithms with the z-series. This sounds like a marketing-gag for an sharpening algorithm to me. Do you have any explanation for this, or is it really just a marketing-gag?
Greetings
Martin
It applies deconvolution sharpening to in-camera JPEGs. It does not affect raw file data.
Do not forget! The size of the exposure field generated by the shutter, especially the short exposure times, also favors the occurrence of diffraction.
That has no practical effect in normal cameras. The blades move, averaging out diffraction effects.
One thing I rarely see pointed out is that diffraction alone is not the only contribution to softening at small apertures.
Light actually reflects off the edge of the iris blades, adding further softening that strengthens as the perimeter-to-area ratio increases.
With odd-blade irises you can observe this by noticing that the diffraction pattern isn’t 180° rotationally symmetrical; opposing spikes have different lengths.
> “With odd-blade irises you can observe this by noticing that the diffraction pattern isn’t 180° rotationally symmetrical; opposing spikes have different lengths.”
The length of the spike is determined by the angle between the blades. Since these angles are very close to 180°, any tiny variation would affect the length a lot.
I do not see how this can confirm (or reject) your claim of “the reflections in the blade” contributing anything significant.
What I’m trying to explain is the phenomenon where on odd-blade lenses (5, 7, 9) opposing spikes are long and short, and the long and short alternate as you go around.
This isn’t random variation, it’s a common pattern.
For example, on the latter two images here it’s very noticeable:
https://www.dpreview.com/forums/post/57639730
It’s less visible on the 100/2.8L shot; perhaps that lens has sharper iris blades with less of an edge to reflect off.
Are you perhaps referring to the overlapping of spikes from lenses with even-blade-count diaphragms?
Another unfortunate issue is that precisely viewing sharpness will vary from person to person depending on their eyes. This may seem elementary but you need to have your eyes checked or at least use some type of correction lens to be sure its not your brain making you think you don’t need glasses.
If your vision from 27″ and closer is NOT in need of any diopter alternating lenses your in luck, I have had issues with seeing sharp images on my computer monitor (blaming the camera and myself) thinking I was at fault or the AF was. At a friends suggestion recently I came to find out that when I put on my glasses the images were indeed tack sharp not the fault of the AF in the camera or me. I just need glasses to make the images pop!!!!
Now if you had your glasses made in the USA the glass used to make the lenses is inferior to glass used outside of the USA its thicker for safety reasons.
My lenses made in Hong Kong are far superior in micro contrast and crispy sharpness to those I had made here in USA and they are the ones I use for the computer monitor.
I don’t know where to start to try to clear this up. Let’s just say that I consider much of this comment “not even wrong”. Google it.