Real and approximated blur profiles

This is a continuation of a series of posts about blur management for landscape photography. The series starts here.

So far in this series, I’ve been talking about blur circles as if they were disks of constant intensity (digital filter designers call these pillboxes). When we’re talking about combining the blur from diffraction, defocus, and the pixel aperture in the camera, they are more complicated than that. In this post I’ll discuss the models I’m using for each type of blur, how those three modeled blurs combine, and the approximation that I’ve been using.

If you’re willing to work with me through a fairly complicated graph, I can show you an example of all that in one plot. I’ll walk you through it after I show it to you.

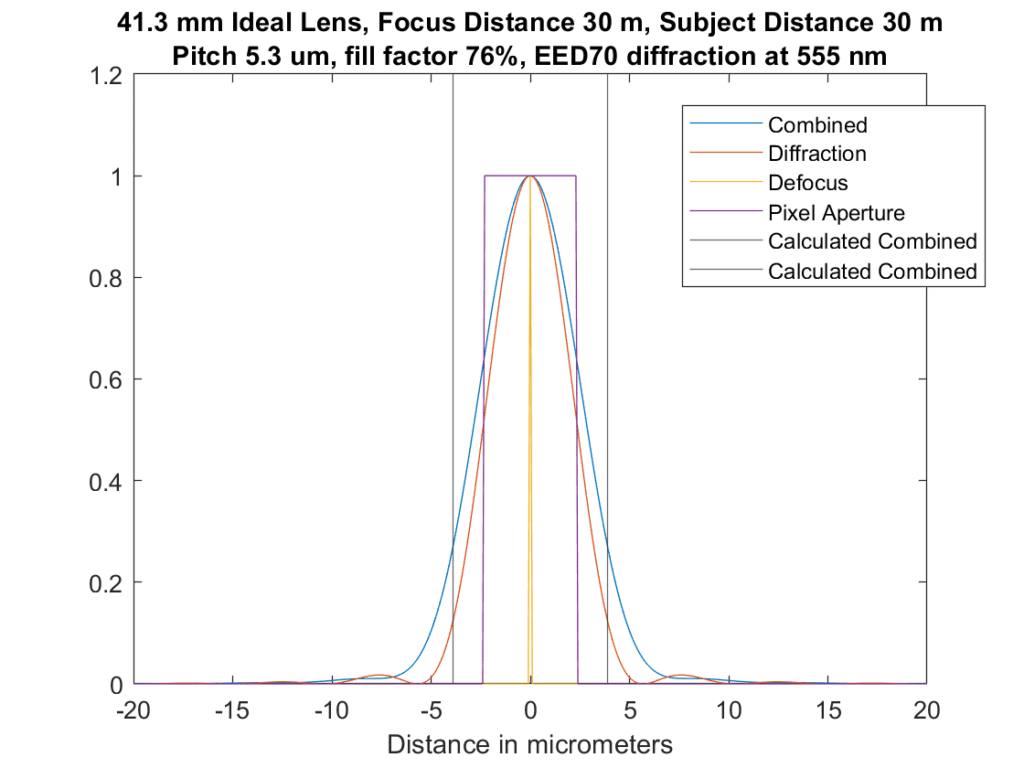
The modeled aperture is f/8. What you’re looking at above is a cross-section of the blurs from each source. The yellow is the defocus blur, and in this case there’s none of that since the subject is perfectly in focus. The magenta box is the blur from the pixel aperture, which is assumed to be a pillbox with a diameter of the pixel pitch times the square root of the fill factor. The red curve is that of the diffraction. I convolved all three to get the blue curve, which is the combined effect of all three modeled blurs. And finally, the two vertical lines represent the limits of the blur circles that I’ve been showing you, using something called EED70 for the Airy disk diameter. The blur circle limits cross the convolved solution at about a quarter of the peak value. There is not much energy outside those lines, but there is some.

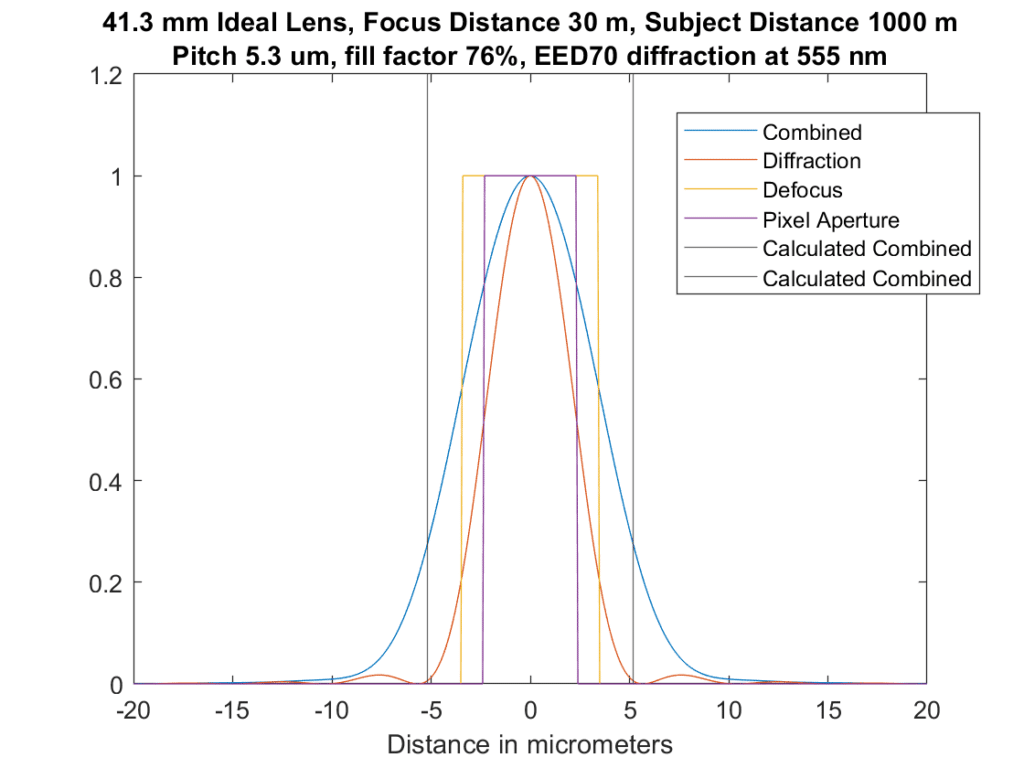
Let’s defocus a bit:

Now we are convolving three things, and the blur is getting worse. The approximation is still crossing the convolved solution at about a quarter of the peak.

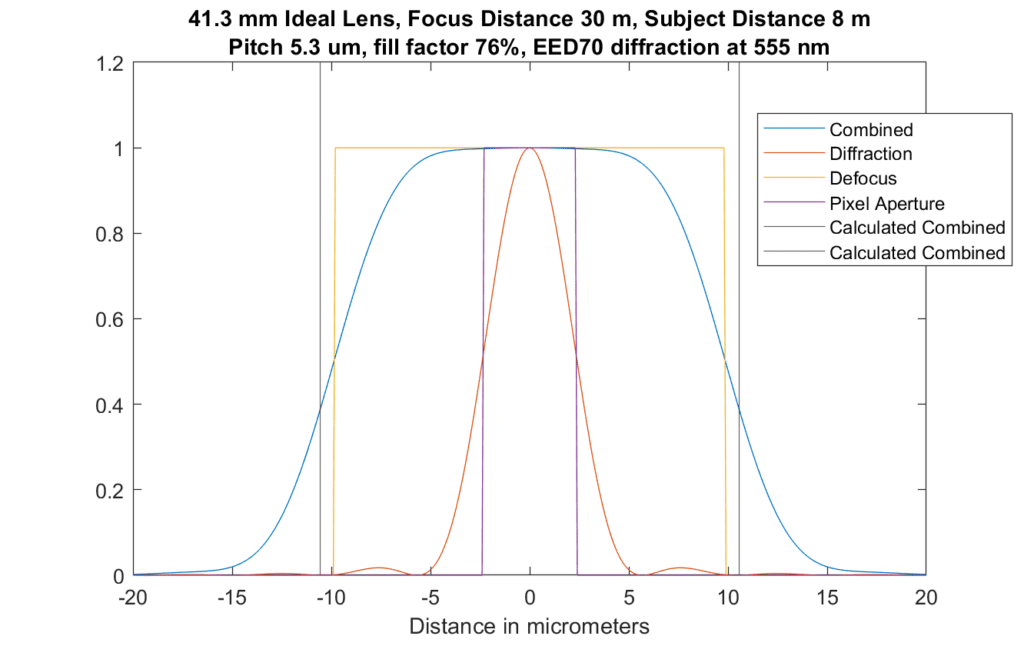
If we defocus far enough that focus error is the primary blur source, this is what we see:

The approximation crosses the blue curve at a point that is higher than with less defocus, but it looks like there is proportionally less energy outside those limits.

I’m pretty comfortable with these approximations. They don’t have to be particularly accurate to be useful, and it looks to me like they are at least as accurate as they need to be.