This is one in a series of posts on the Fujifilm GFX 100S. You should be able to find all the posts about that camera in the Category List on the right sidebar, below the Articles widget. There’s a drop-down menu there that you can use to get to all the posts in this series; just look for “GFX 100S”.
In this post, I showed you histograms for a series of dark-field images made with the GFX 100s. A reader requested that I look at the histograms when the camera is set to 16-bit precision. Hence, this post.
I made images with the body cap in place under the following conditions:
- EFCS
- 1/1000 second
- 16 bit
- Lossless compression
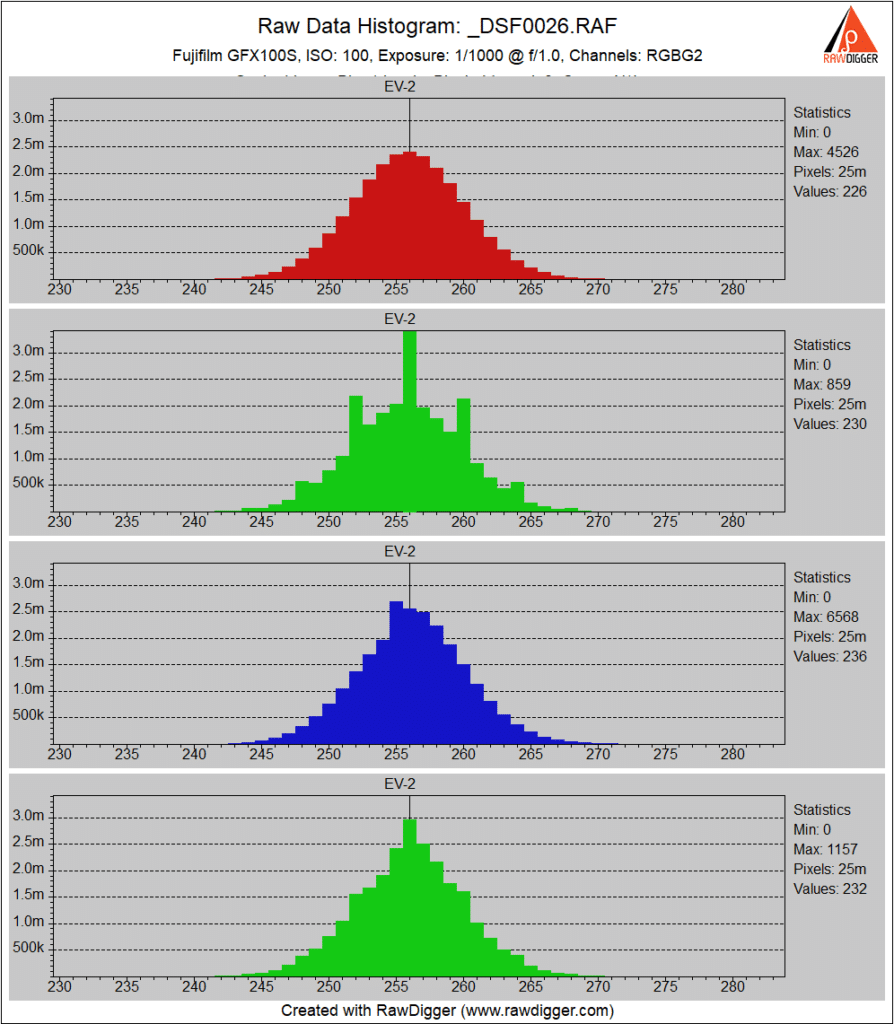
At ISO 100, we see some combing in the first green channel histogram. I’m not sure what’s going on there. One of the third from the LSB transitions is a bit wider than it should be. The black point is about 256.
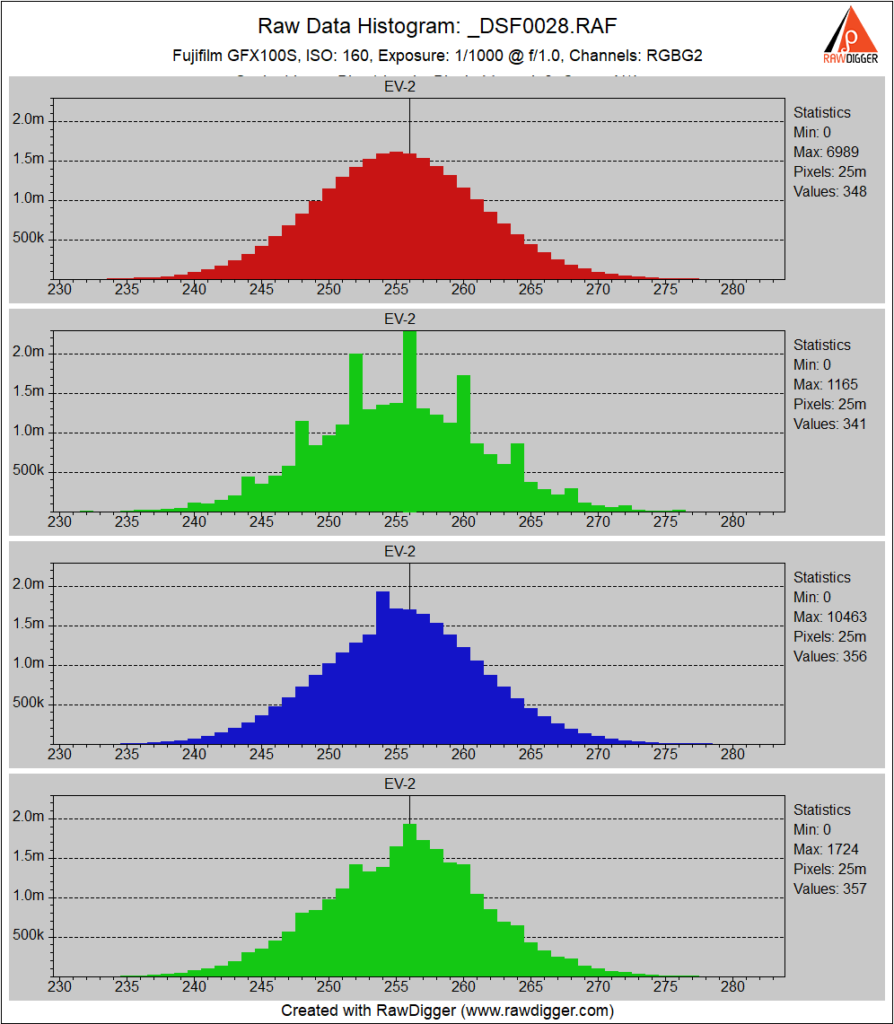
At ISO 160, we see the same first green chanel combing, and also the same blue channel peaking that I attributed to PDAF pixel interpolation in the first set of histograms. The blue channel black point seems to have shifted a bit lower.
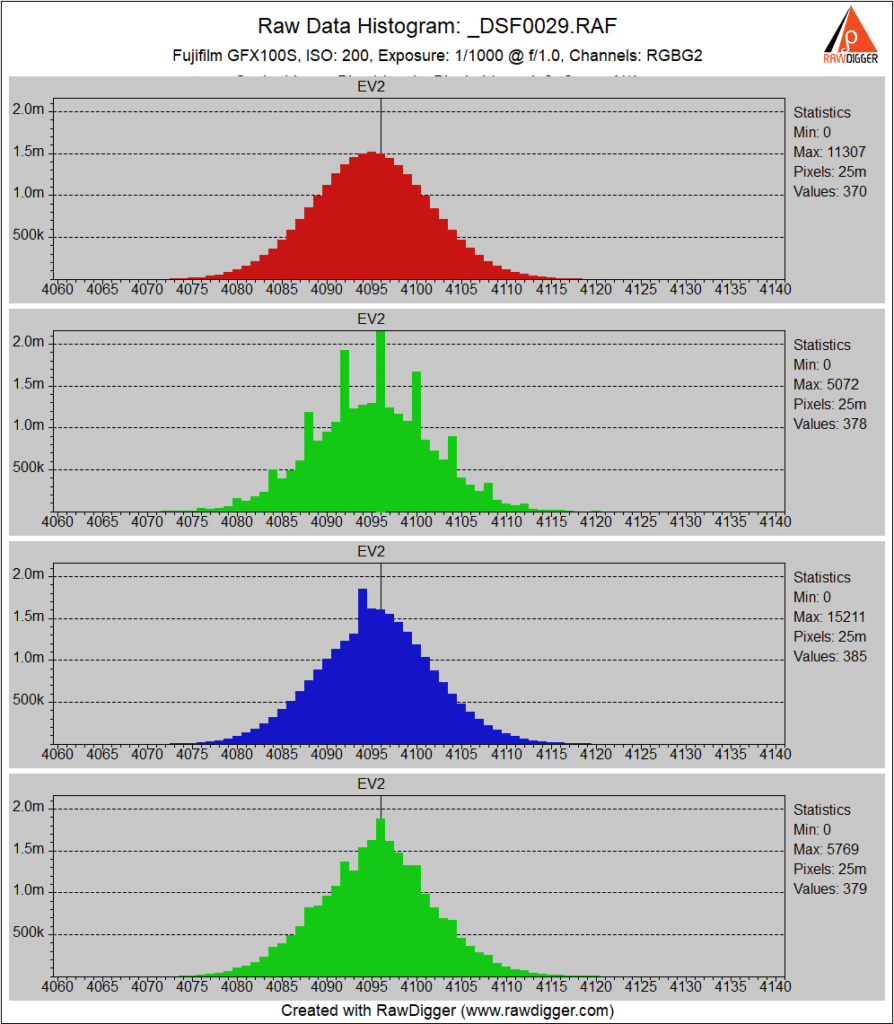
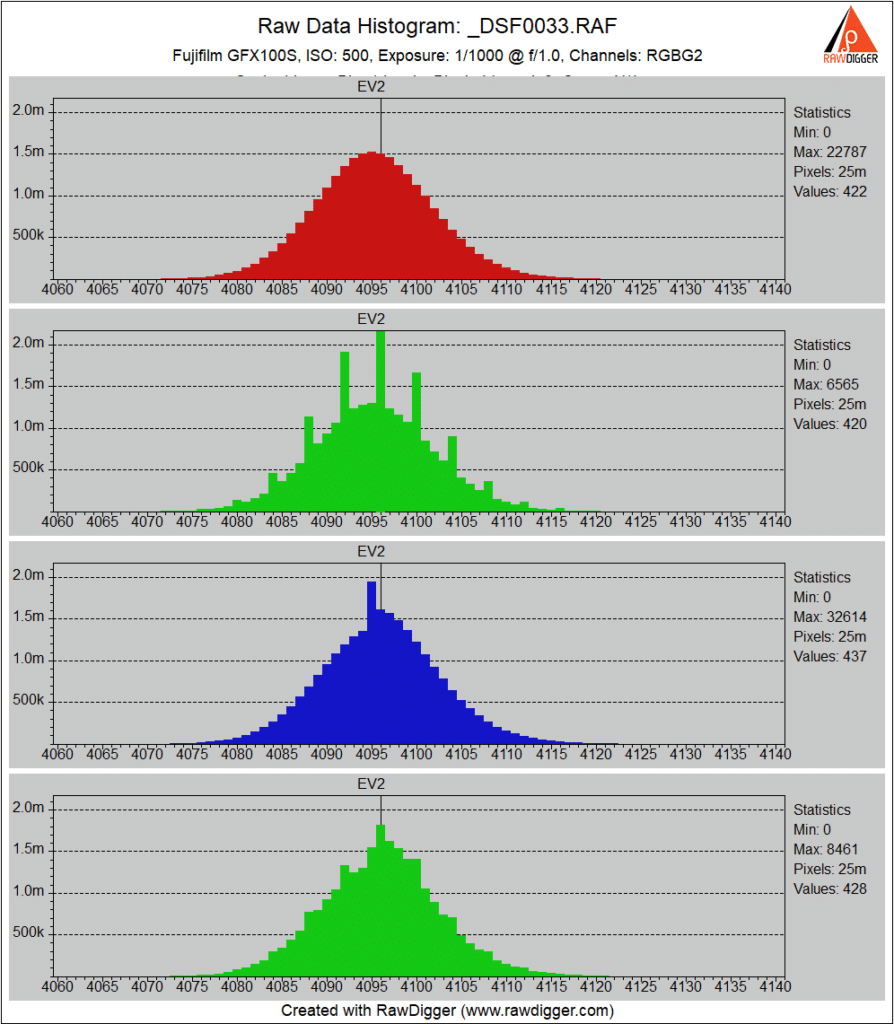
At ISO 200, the black point changes to about 4096.
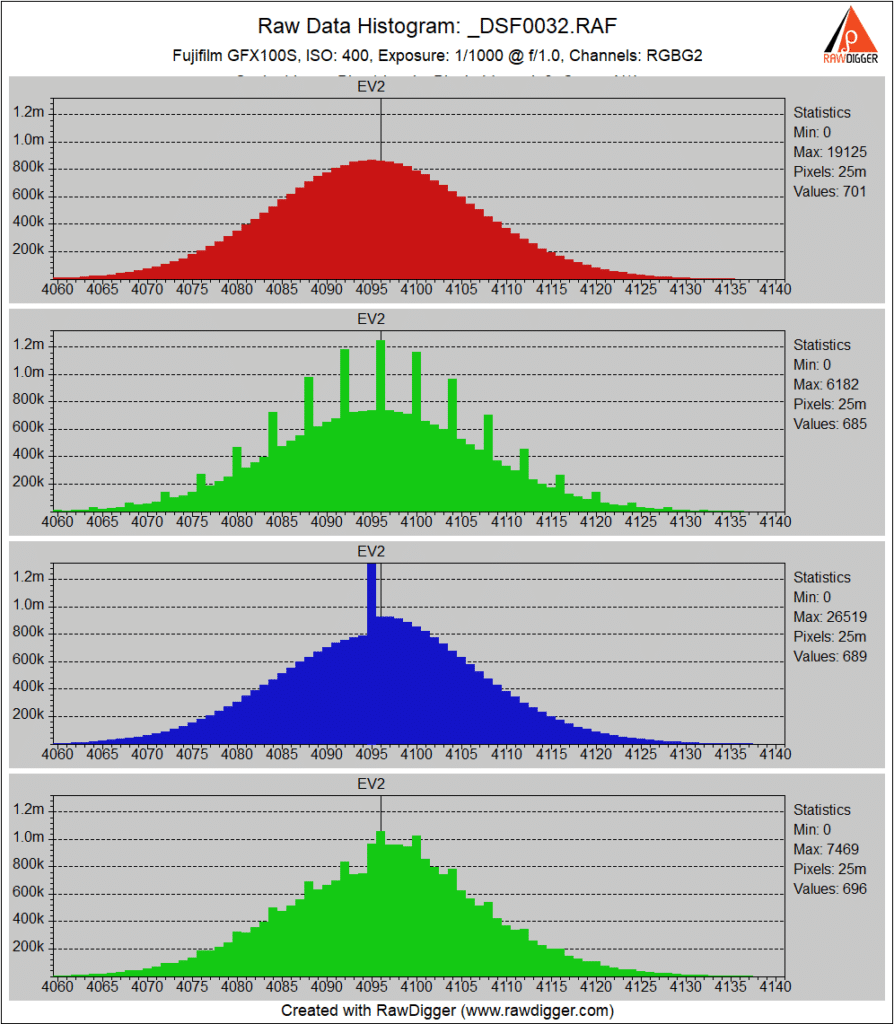
ISO 400 is the highest ISO with the low conversion gain. Some combing is emerging in the second green chanel histogram.
ISO 500 is the lowest ISO setting with high conversion gain, and the change in conversion gain results in a decrease in the read noise.
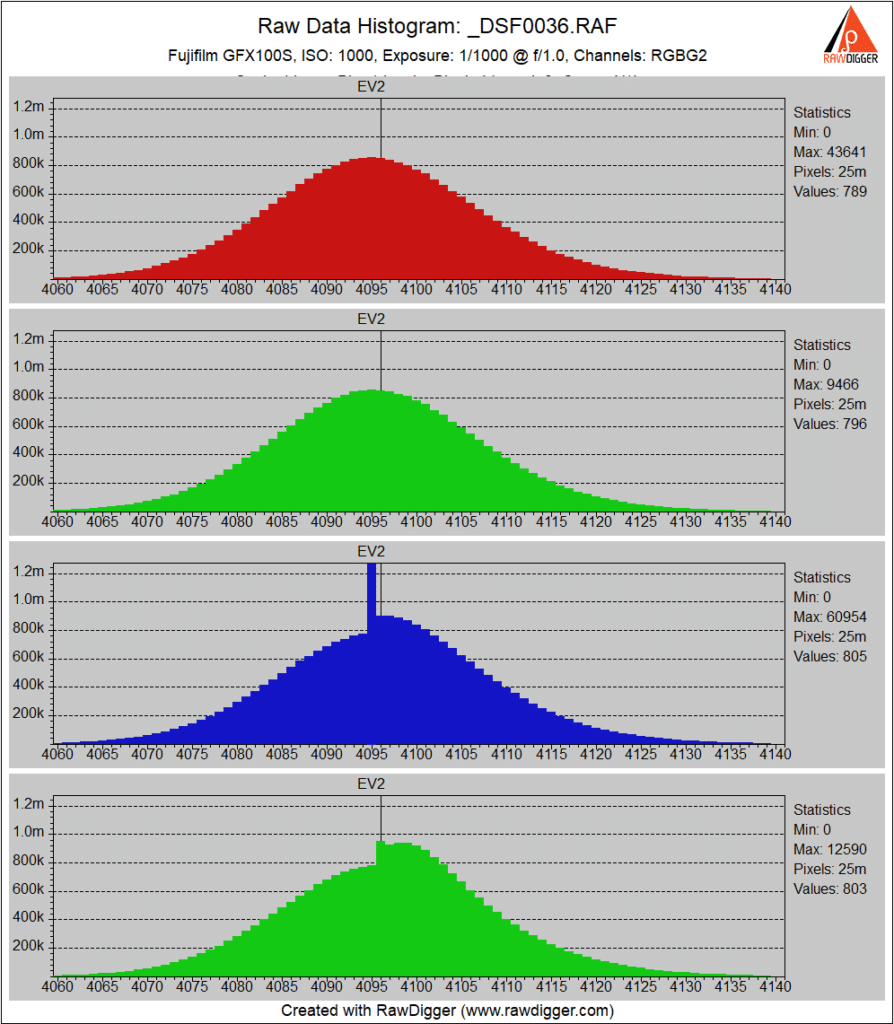
At ISO 1000, the combing in the first green channel disappears. It’s obvious that there is some kind of signal processing in the second green channel.
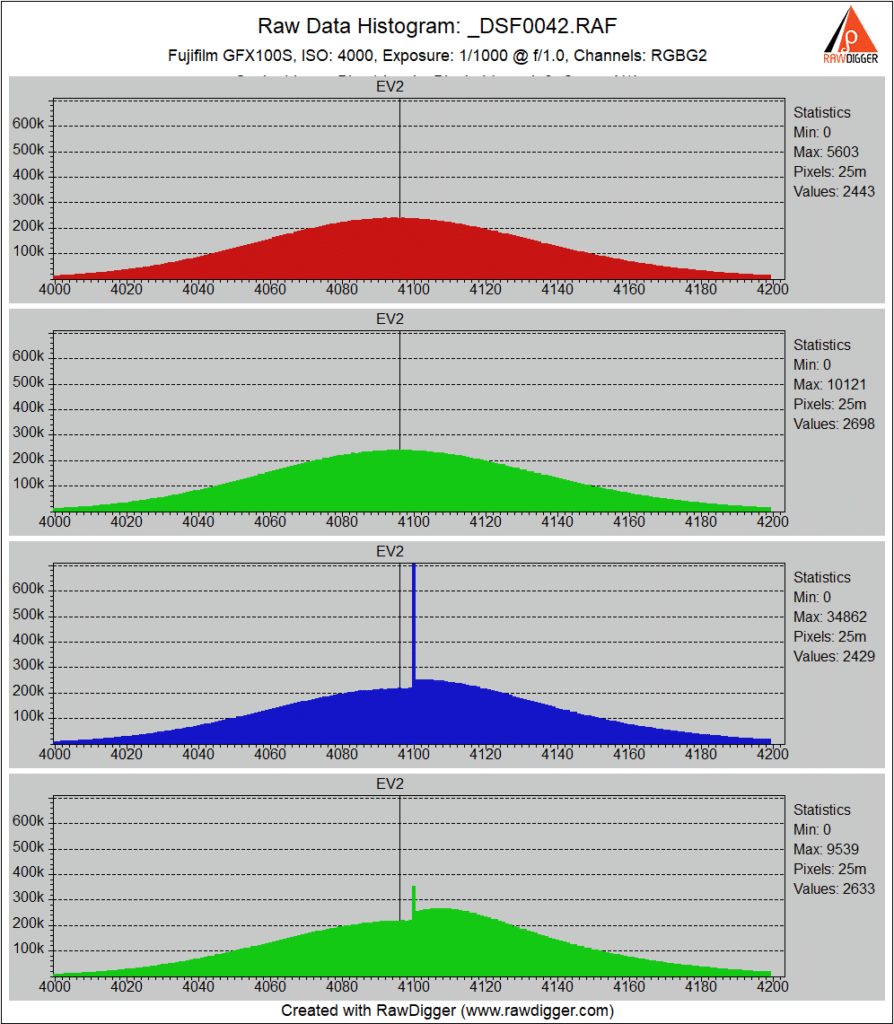
At ISO 4000, the red and first green channel histograms look perfectly normal. The interpolation is evident int he blue and second green channels, and the black point has shifted a bit higher in those channels.
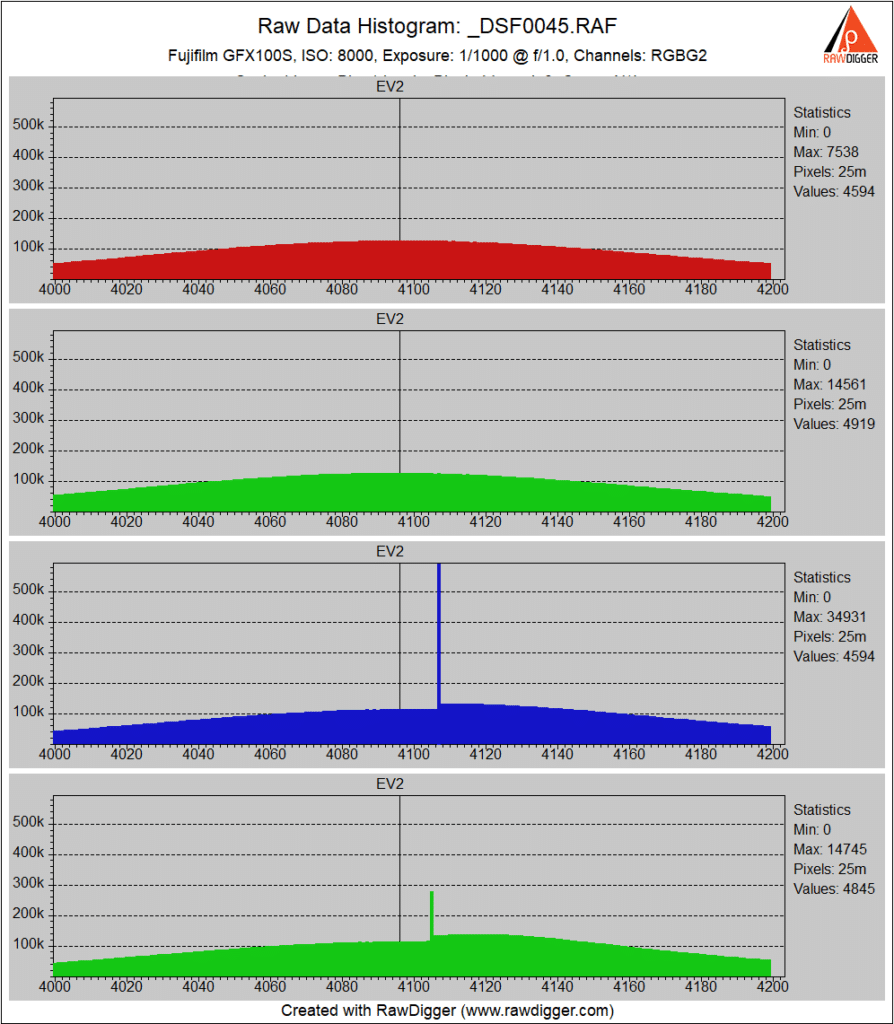
At ISO 8000, the second green and blue channel back points have shifted even higher.
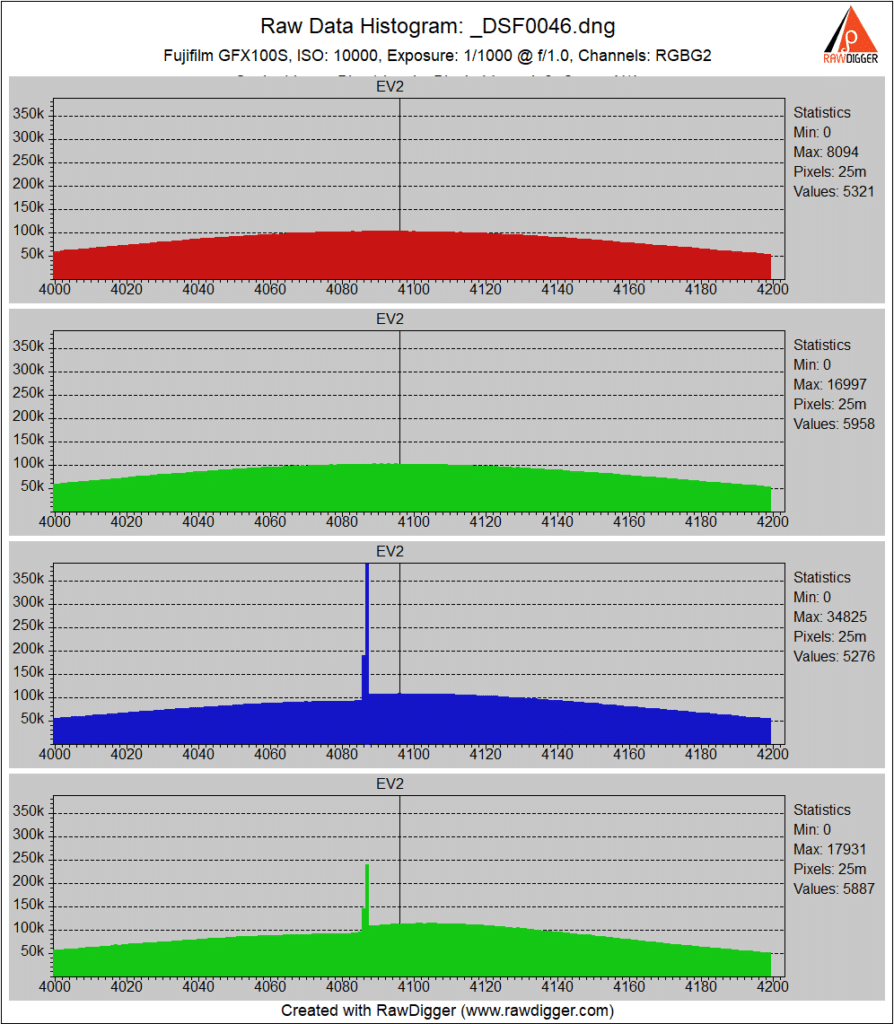
At ISO 10000, the black points of the second green and the blue channels have shifted to less than their nominal values.
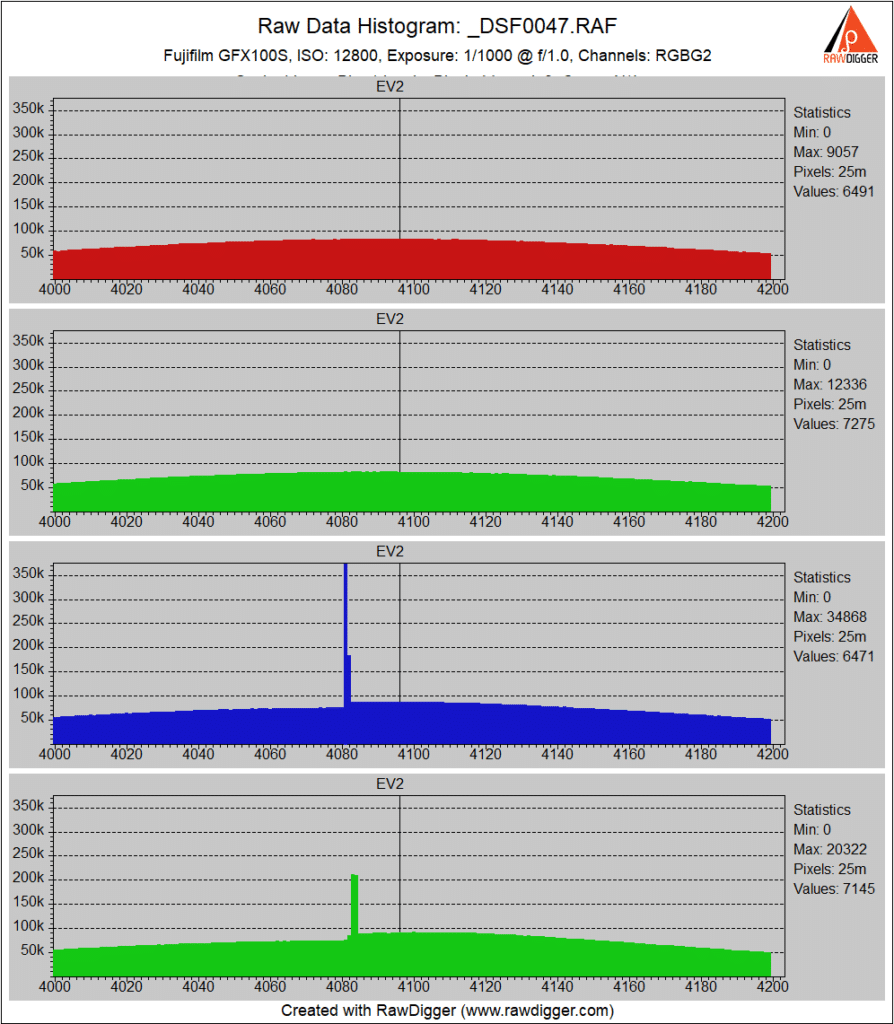
Same at ISO 12800.
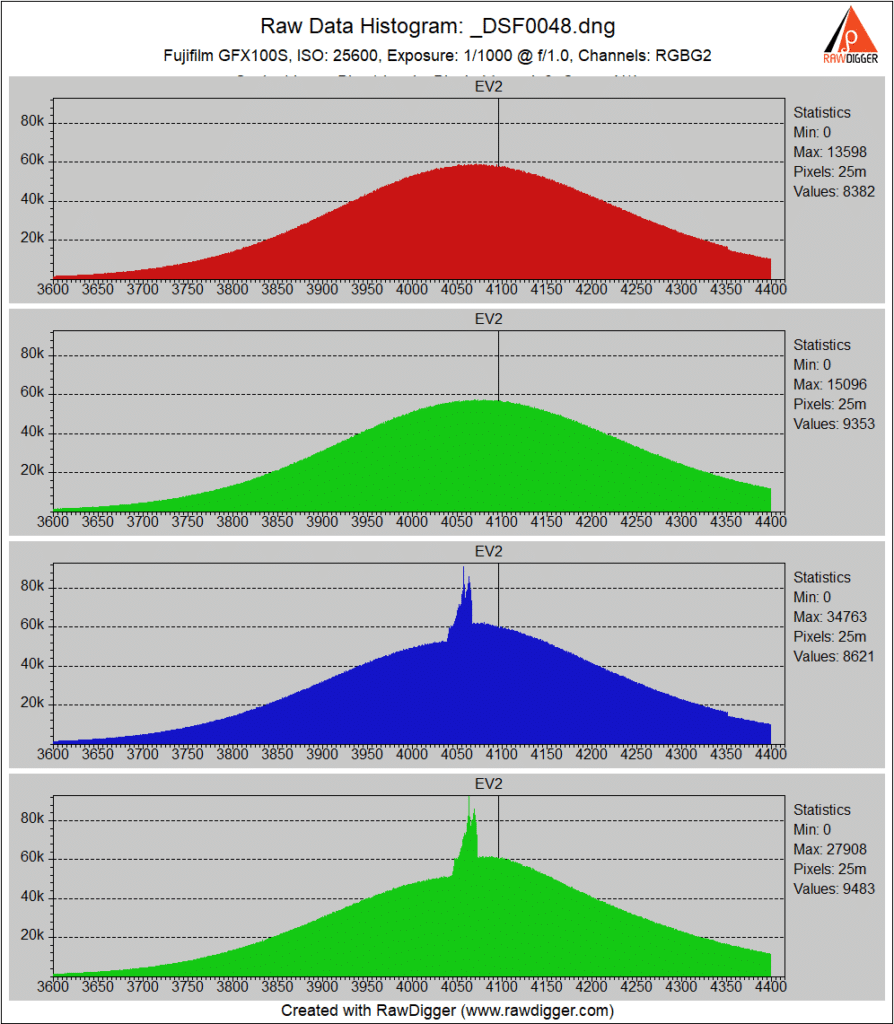
At ISO 25600, the noise is so great that the interpolation spike is widening.
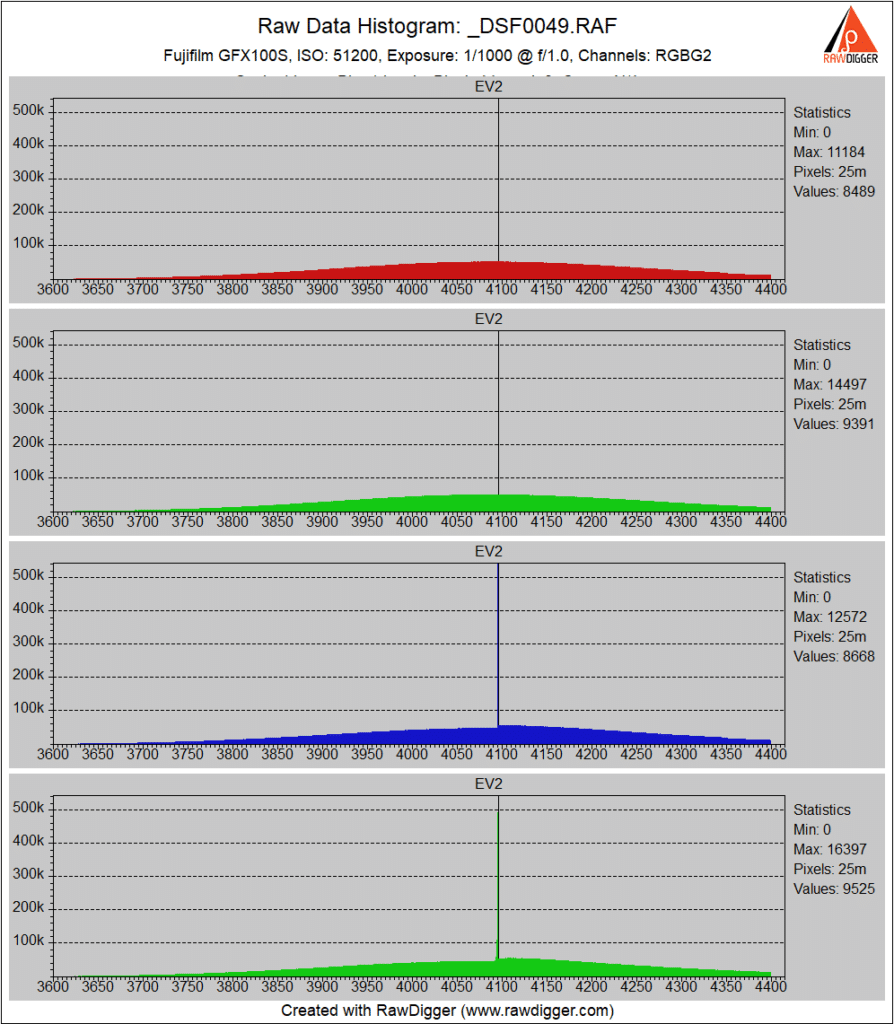
At ISO 51200, The interpolation spike is now just one-bucket wide.
This has been an interesting exercise. It remains to be seen how these results relate to real photography.
> “One of the third from the LSB transitions is a bit wider than it should be. ”
No, it is 1 out of 4 values. It seems that about every 8th–10th sensel is read in 14-bit mode, and is converted to 16-bits. (???!!!)
Thanks for your measurements!
Every fourth value implies the third bit counting from the LSB.
[Addition…]
Suppose one selects the G1 pixels with DN≡256 from you ISO=100 image, then inspects where they are positioned. Then about 40% of these pixels are going to be “the mysterious 14-bit pixels”, and the remaining 60% are going to be scattered at random.
I suppose that if there is a pattern in the positioning of the “mysterious” pixels, this pattern will be recognizable even with the 1.5× stronger noise…
[Addition²…]
Another idea: if one combines about 5 images and selects G1 pixels with values divisible by 4, then (assuming that the “mysterious” pixels are not random) every “mysterious” pixel will be selected 5 times, while most of the remaining pixels will be chosen 3 times or less. This way one can reduce the S/N ratio of “mysteriousness” to very high values…
Do the actual black points drift with time and/or temperature?
Are they the same between copies of the camera?
I know some cameras have masked pixels on the sensor that act as a reference point for black levels, but I don’t know if this is true for Fuji.
“At ISO 100, we see some combing in the first green channel histogram.”
That could be the result of some pre-conditioning with a factor less than 1.
Possibly, but at 16-bit precision that sounds like it wouldn’t accomplish much. It’s in the 14th bit.
… Then the factor must be 0.8 with very high precision. Moreover, then the peaks would be at even values not divisible by 4 — as opposed to the observed “values divisible by 4”.