This is a continuation of analyzing the process variables involved in doing UniWB from an LCD monitor with only Rawdigger and Photoshop as the software tools involved. This post is statistical, technical, and nerdy. It is presented in the spirit of giving the interested reader to tools to replicate what I’m doing. If you’re just interested in the results, skip this post.
To find out how significant the positional color shifts are, we need to find the relationship between color shifts in solid colors on the monitor and coefficients in the resultant white balance. There is no reason to think that this is a linear relationship, but in the spirit of looking for the keys under the lamppost, we’ll press on with an analysis that assumes linearity.
Before we get to the effect of small color shift on the white balance coefficients, we first need to deal with the possibility that there might be some noise in the camera’s processing of an image when it creates a new white balance from an image. You’d think the process would be totally deterministic, and maybe it is, but I thought I should check.
I asked the D4 to do white balancing from an image and fired off a shot. I did that three more times, using the same image each times. I read the four exposures into Rawdigger, and looked at the EXIF data. The numbers were identical.
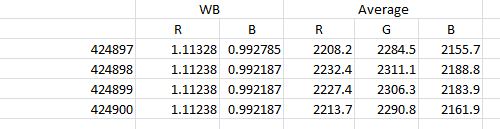
The next test was to make four photographs of identical solid blocks of color and have the camera white balance to them. This test produced a real surprise for me. In spite of the usual random variations in the average values of the four shots from which the white balance was computed by the camera, the white balance coefficients were identical:
The above results worry me. Can I count on the camera to respond in a linear way to changes of the colors of the image to wh9ch it is white balancing? Probably not. In spite of that potential large problem, I pressed on. I set up a full frame solid color ring-around, with R=93, G=64, b=85 in the center and steps of three units in each primary. In all cases, the white balance coefficients were the same:
This explains why I couldn’t get the white balance coefficients down to where I wanted them without tweaking the settings after I white balanced to an image. I tried to balance to an extremely different color, R=110, G=120, B= 100, and got the same coefficients. The colors look quite different in the four-image picker during the dialog that you use to white balance to an image, but the coefficients are the same. Weird. Just to double check, I varied the color temperature in the dialog that you use to white balance by color temperature and color offset, and sure enough, the coefficients changes in ways that appeared to make sense. I also tried the preset white balance settings and saw the coefficients change there as well? Is the D4 unique in ignoring some pretty considerable differences when it white balances to an image? Only one way to find out.
I took the NEX-7 and fitted it with a 90mm Nikon-mount lens, using a Novoflex adapter. With the 1.5 multiplier on the Sony, that gave me the same angle of view as the 135mm lens on the Nikon.
I white balanced to two close-together color screens, and one quite a ways off. I used the same ISO, f/stop, shutter speed, and defocusing that I’d used with the D4. The first two colors were were R=93, G=64, b=85 and R=93, G=64, b=90, and the distant one was R=110, G=120, B= 100. The camera complained about not being able to white balance the first two, gave identical color temperatures and offsets, and, when I took a picture of the target, showed it as a neutral gray, just as it should. The camera didn’t complain about balancing to the sickly green color.
Here are the results:
They appear to make sense. We’re too far from the NEX-7’s UniWB point to judge sensitivity to small positional variations in the screen RGB values. We’ll have to bring out the big-step target and see shat we get.
Here’s an image of the target in Rawdigger with the upper left corner set to R=120, G=70, and B=80, and steps of 10:
Here’s the best rectangle:
And here are the values for that rectangle:
Going back to Photoshop , looking at the target, and counting 7 over and 6 down, we read R=180, G=70, B=130.
Turning off the Steps of 10 layer and tuning on the Steps of 2 layer, and setting the upper left corner to R=170, G=70, B=120 and taking another picture, we get this image in Rawdigger:
Here’s the most neutral rectangle:
And here are the values:
Counting 4 over and 6 down on the target in Photoshop and hovering the cursor over that square, we read R=176, G=70, B=130.
Putting that value into the solid color layer and taking another image, we get these averages in Rawdigger:
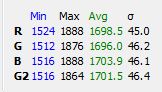
Telling the NEX7 to white balance to the target, we get the following values:
This looks very good.
Before we can see if our positional variations create significant shite balance variations, we need to see if the camera is capable of delivering consistent exposures. This is similar to what I did with the D4 at the previous post, except, since the NEX-7 doesn’t have an intervalometer, I just cranked off 19 exposures of the target. Also, there is no diaphragm variation with the NEX-7, since the Novaflex adapter I used does not support an automatic diaphragm. Since the exposures were made over a short period of time, there might be less monitor variation than with the D4 test. Here are the results:
The red and green numbers look just a tad worse than the D4, but the blue is twice as bad. We’ll keep this in mind when we get to the white balance sensitivity study. I looked for any sign of heating of the sensor causing a systematic variation over the series, but if it’s there, it’s extremely weak.
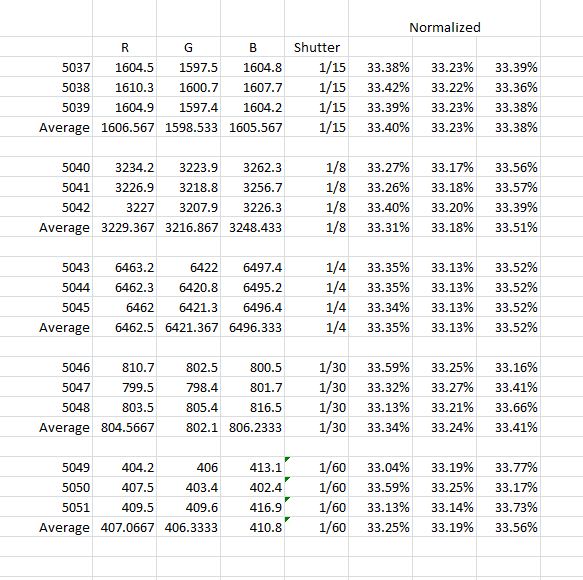
While I was at it, I made a set of measurements of the same target at different exposures, with three images at each exposure. If the camera is perfect, the ratios between the red, green, and blue values should not change. Here’s what I saw:
This shows that the camera is behaving as expected, that exposure makes little difference in white balance, and, incidentally, that the NEX-7 shutter has high relative accuracy.
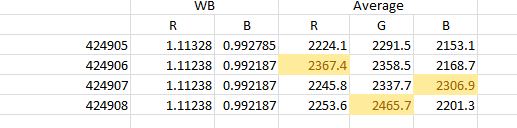
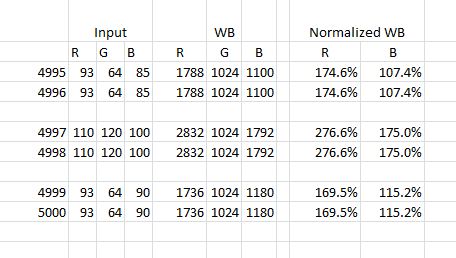
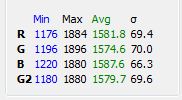
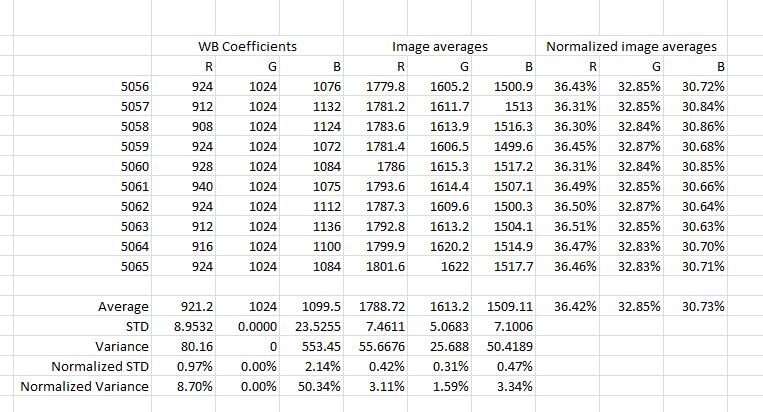
To get an idea of the repeatability of the white balance from shot calculations in the NEX-7 I cranked the blue down two units from our center point (hoping to get closer to dead on, but you’ll see that I went too far – it doesn’t affect what we’re looking for with this test). I white balanced to the screen, made and exposure, and repeated for a total of ten exposures. I then looked at the white balance coefficients that the camera came up with, and at the RGB values in the images. Note that the RGB values can only be compared to the WB coefficients in aggregate, since they are the results of two separate exposures. Here are the numbers:
My conclusions? First, the fact that all of the camera-calculated coefficients are divisible by four makes me think that it is only capable of that level of precision, which translates to about one part in 256, or 0.4%. Second, the variability of the image samples, especially the blue, leads to a significant variability in the in-camera calculated blue white balance coefficient. Since the standard deviation of the blue WB coefficient is a little over 2%, I think it would be unwise to attempt to achieve WB coefficient accuracy to better than two standard deviations, or a bit over 4% in a non-iterative WB process. We can get an idea of how many samples we’ll have to take in a sensitivity study to get any desired statistical accuracy. For three- sigma accuracy of one percent in the WB coefficients, we’ll need 16 samples per data point.
And fourth, by looking at the difference in per=color image pixel averages and comparing that to the deviation of the WB coefficietnts from perfection (all the same), we can get an idea of the sensitivity of the WB coefficients to image data near RGB balance. Here’s the data:
The sensitivity is very close to 100%. However, that doesn’t square with the normalized standard deviations of the WB coefficients being so much higher than the normalized standard deviations of the image data. The fact that the green WB coefficient is held to unity will make the WB coefficients have a slightly higher standard deviation, but the increase should be on the order of 50%, not double in the case of red, or four times in the case of blue. I could pursue this, but I think I’ll let it be, at least for now.
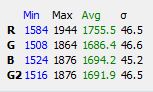
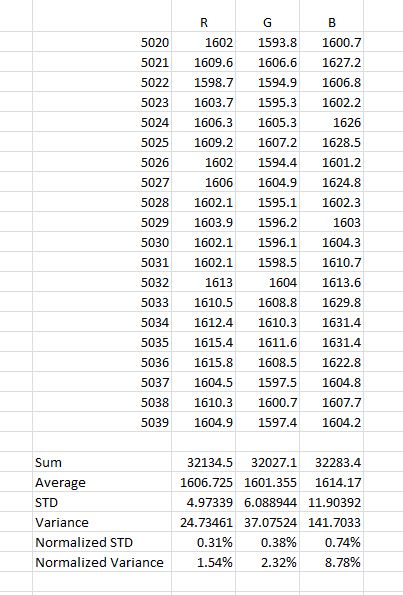
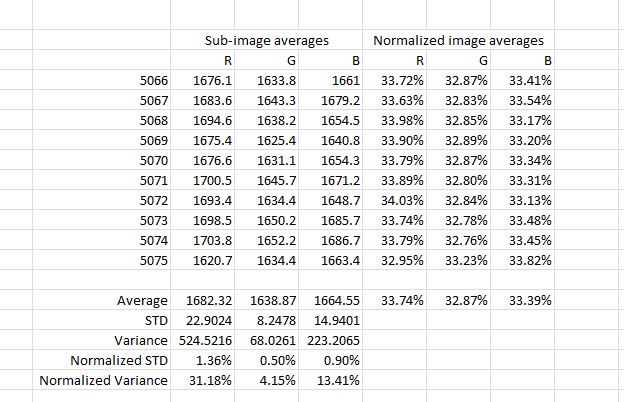
The last little bit of testing I need to do is to discover the statistics of sampling the sub-rectangles of the 10×10 gridded test target. You’d expect the variance to be substantially higher than the full-screen solid-color statistics because the sample size is smaller – about 1/200th as large. I aimed the camera at the 10×10 grid set up for zero variation and made ten exposures. I brought the images into Rawdigger, set up a sampling rectangle within one of the grid positions, and looked at the statistics of all ten images. Here’s what I saw:
There is some spreading because of the smaller sample size, but it’s not as bad as I feared.
We now have enough data to make an estimate for the NEX-7 of how close we can expect to get to equal WB coefficients in a procedure with no iteration, such as shoot a coarse target, shoot a fine target, shoot a full-screen solid-color block, and white balance to that.
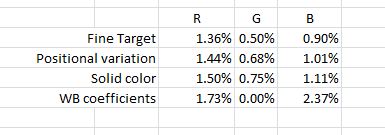
I can’t show you my work on this one, because I used a specialized tool from Frontline Systems, an Excel plugin called Solver. Solver allows you to do statistical modeling. I used it to model the entire chain of the proposed UniWB process based on the statistics that I’ve measured in this post, plus the positional statistics from the previous post. I assumed that the errors of measuring the coarse target had no effect, since all the coarse target does is get you to the right fine target. The statistical chain starts with the spread of the RGB values in the raw file when that target is photographed and I assumed a Gaussian distribution. That spread is passed through the spread do to positional variation, for which I assumed a uniform distribution – it doesn’t have long tails like a Gaussian variable. That spread is further passed through the camera’s WB statistics – assumed Gaussian – to get the final statistics for the overall WB spread. I simulated the quantization of the WB coefficients that the NEX-7 does, but found to my surprise that it doesn’t add much at all to the overall spread, so I let it out of the model. For completeness I modeled the RGB variations we are likely to find in the raw file of the final, solid color, image. I ran the model 100,000 times, which took a few seconds, and computed the normalized standard deviation of the results. Here they are (the numbers are cumulative — each includes the spread of the preceding step in the chain):
My conclusion is that we should expect WB coefficients to be within about 5% ( about two standard deviations) of equal values when using this technique with the NEX-7. My test run (documented above) gave substantially better results. Call that good luck. Five percent should be plenty good enough; I have noticed that it’s hard to see differences in the in-camera histogram even with 10% differences in the WB coefficients.
Whew! That was a lot of work, and I didn’t even do a proper statistical analysis — a real one would have required far more samples, and I spent a lot more time on this than I wanted to as it is. However, in spite of my lack of rigor, I think the numbers are close enough for me to have confidence that this is a technique that will yield results that are accurate enough for the intended use.
I still have a problem with the Nikon D4 results. I will look at another Nikon and see if I see something similar. I will also test some non-Nikon, non-Sony camera to see if the technique works, but I won’t do a statistical analysis like the one in this post. If all that goes well, I’ll post the target file in all its many-layered glory, along with instructions for its use.





Leave a Reply