In a private communication, Iliah Borg, one of the early proponents of, and an expert on, UniWB wrote to me: “Suppose you are displaying some grey on your monitor, shoot it …and white-balance the shot. Now if in linear space you multiply the R and B by the resulting custom WB coeffs you should have a magentish square. Taking WB from that square should bring you into ballpark for UniWB.” This is not the first time Iliah has helped me on this project. I applaud his generosity, and I am grateful.
There are two ways to think of this approach to UniWB. The first is as an analytic, deterministic, two-step solution. As such, it may get you close enough for many purposes. For it to be exact, the entire system needs to be linear with no color channel crosstalk (see below for details). The second way to think of this is as the basis for an iterative process that can get you as close as you’d like, except for noise in the system. This way of thinking about the approach is an application of Newton’s Method, where a nonlinear system is assumed to be linear to calculate the next approximation, then measurements are made at the new point and linearity is assumed to calculate the next approximation, and so on. Iliah’s suggested approach employs Newton’s Method in two dimensions simultaneously.
I gave it a try. I set up a target with the Adobe (1998) RGB primaries and white point, but with a gamma of one. With the D800E, I made several iterations, keeping track of the average of the raw RGB values and the EXIF coefficients as I went along. I did some calculations on the raw RGB values to calculate the coefficients from them, so I could compare them to the coefficients that the camera calculated. It’s important to note that the two coefficients are calculated from two separate exposures, since the camera does not store the exposure it uses to calculate the white balance coefficients.
Here’s what I saw:
First, the good news. The coefficients computed by me from the raw image data are very close to the ones that the camera came up with, especially if you consider that they are the result of different exposures. Second, the process seems to be converging. In fact, unless you are really picky, you’d say I was close enough for any reasonable purpose on the fourth iteration.
The bad news? The process is not converging as fast as I think it should, especially at the end. Newton’s method is thought to have quadratic convergence near a zero, with the number of significant digits doubling every step. I don’t see that. Some of it is because of the noise in the monitor photographing process, but there’s something else wrong, too; look at the way the green values in the raw image are going up even though the green value in the monitor color space is not increasing. This means that the green sensor in the camera is responding to some part of the spectrum of the red and/or blue monitor pixels. A communications engineer would call that inter-channel crosstalk, and it is slowing convergence, in essence forcing the algorithm to chase a moving target.
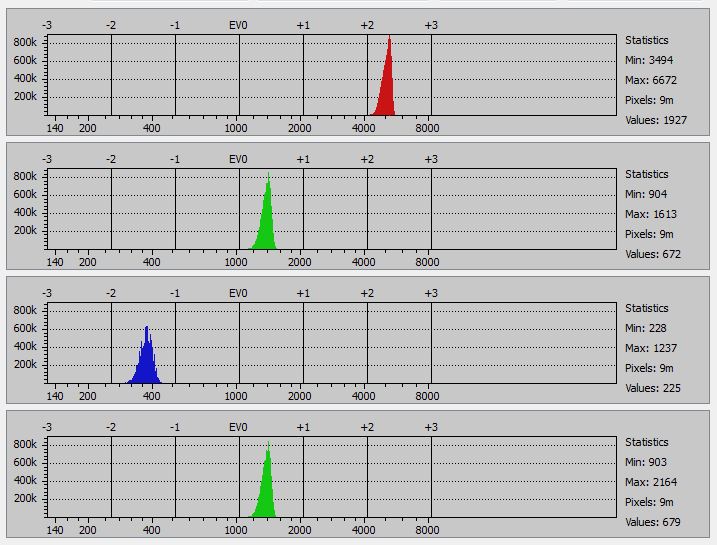
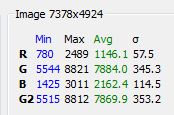
I decided to see if I could characterize the crosstalk. I looked at the raw histograms of pictures of the monitor. First, with R=255, G=0, B=0:
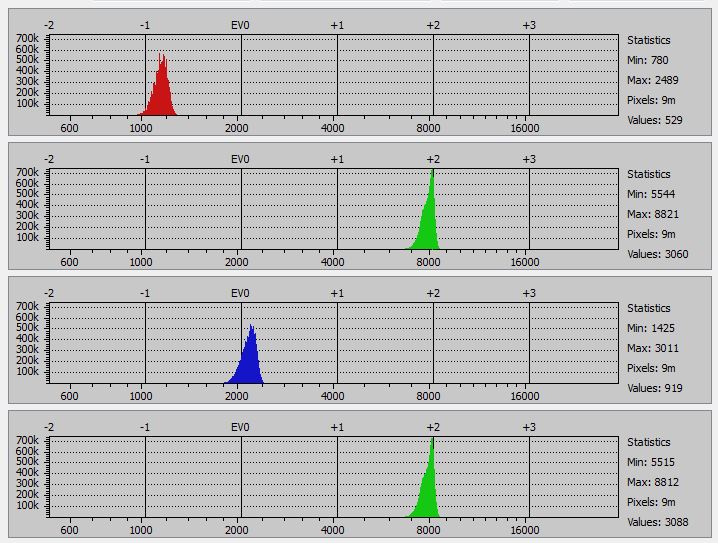
Second, with R=0, G=0, B=255:
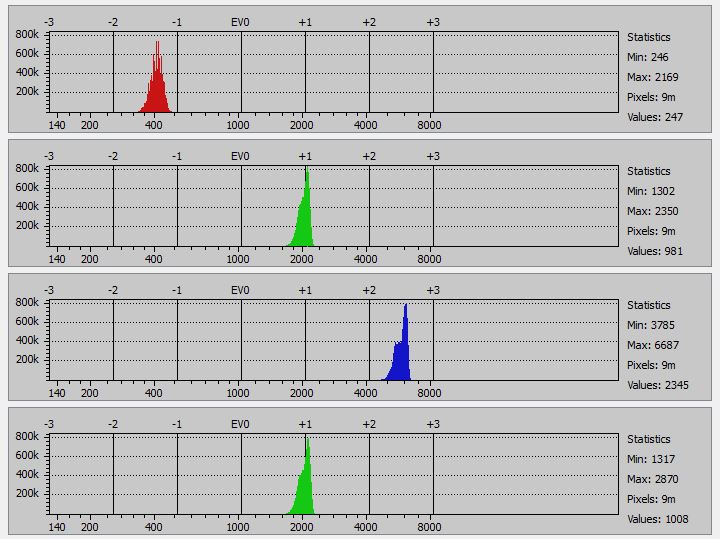
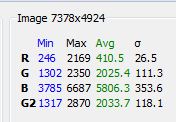
And last, with R=0, G=255, B=0:
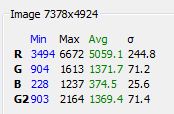
The crosstalk is evident. We can characterize it by looking at the averages for each image. First, R=255, G=0, B=0:
Second, with R=0, G=255, B=0:
And last, with R=0, G=0, B=255:
So, instead of seeing this relationship:
With the subscript c representing the camera values and the subscript m representing the monitor values, we have something more complicated. Using measured camera values for the monitor single-primary targets, we can surmise the relationship is more like this:
We can get a test of this by plugging in the monitor primaries that gave us a nearly unitary white balance from above.
Pretty close. But we really want the equation to work the other way around; we want to know what monitor primaries to use to get the desired raw values in the camera. So we need to invert the square matrix above, getting this:
Checking our math, with a few more significant figures than I’m showing you, we get:
Then our Newton’s Method algorithm, expressed in raw camera values, can be stated this way:
Or, in terms of the monitor values, like this:
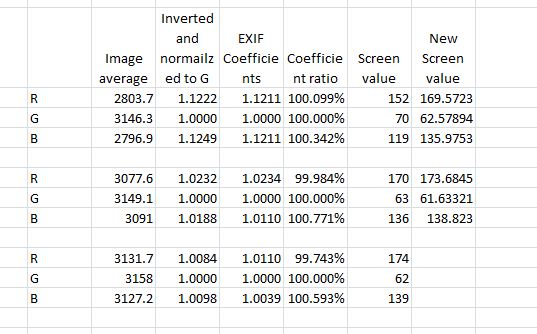
Trying the above on the D800E, we get this:
Not bad. Within about 2% on the first iteration, and less than 1% on the second. If you look at the way the numbers change with each iteration, you can see the algorithm removing green in monitor space so, with the crosstalk into the green channel that comes with increasing red and blue in monitor space, the amount of green in camera space remains approximately constant.

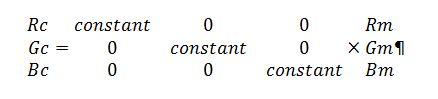


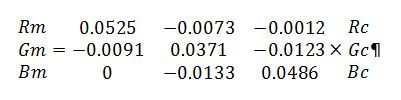

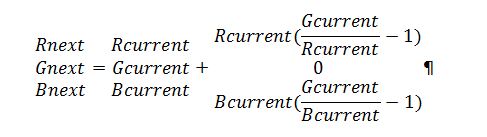

Iliah Borg writes:
“Your part 20 is very good. I really enjoyed reading it. It is solid and impressive work that you are displaying.
You may want to try to look at your monitor primaries (extracted from monitor matrix profile) to see if you can come up with a simpler way to calculate the correction matrix. But I guess a generalized experimental method of computing the correction matrix may prove to be more useful. Also, what comes into the play here is the spectral transmission of the CFA on the sensor. It contains overlapping curves for red, green, and blue channels; those curves are responsible for a sort of channel cross-talk.
I’m not hiding my name, you can of course reference it whether you are proving or disproving the points I’m making.”
Thanks, Iliah. You told me that you did your testing in the native monitor primaries, and I didn’t think through the implications of that. If the color management software has to mix the native primaries to achieve the Adobe RGB primaries, that’s a possible source of crosstalk. I don’t think it’s too important in my case, since the PA301W primaries are very close to the Adobe RGB ones. Of course, now that you mention it, I’ll have to run a test.
I think the CFA filters are more likely the main crosstalk source, but the monitor dyes could play a role.
And thanks for all your help on this project.