I took the 256 megapixel, 16-bit per color plane image filled with uniformly-distributed random colors that I used for the previous post, and performed iterative color space conversions in Matlab from sRGB to Adode (1998) RGB and back, measuring the errors in CIELab Delta E after each round trip. Because the image was so large, I used either 2000×2000 or 4000×4000 pixel crops from the upper left corner. I did not recreate the image for each run; the colors started out the same.
If we convert the image from double-precision floating point to 16-bit unsigned integer representation after every color space conversion, we get worst-case errors that look like this:
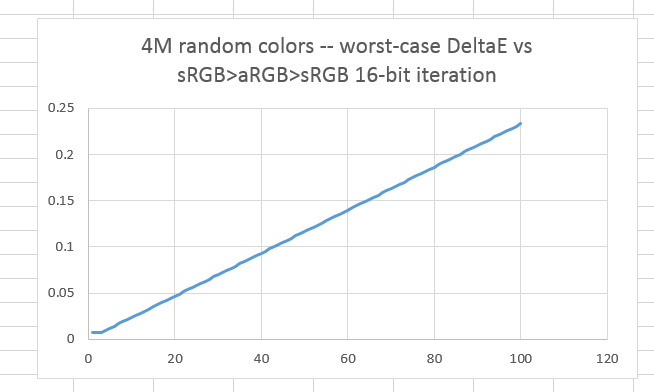
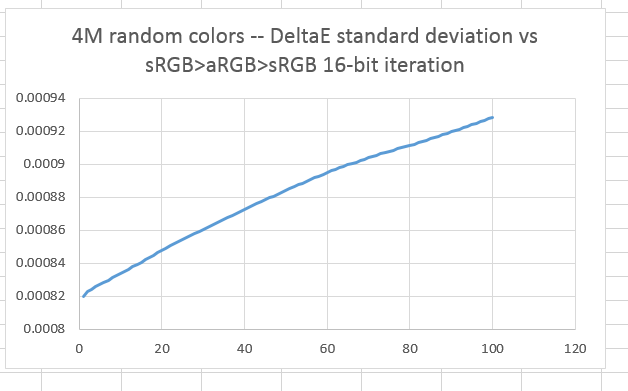
The standard deviation of the errors:
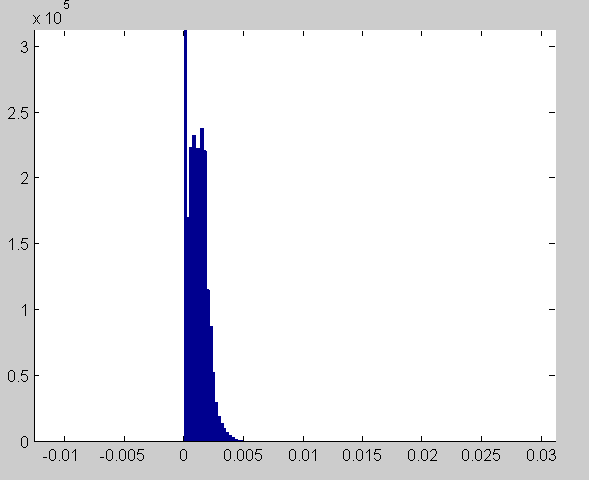
Here’s what the histogram of the Delta E error image looks like after 100 iterations:
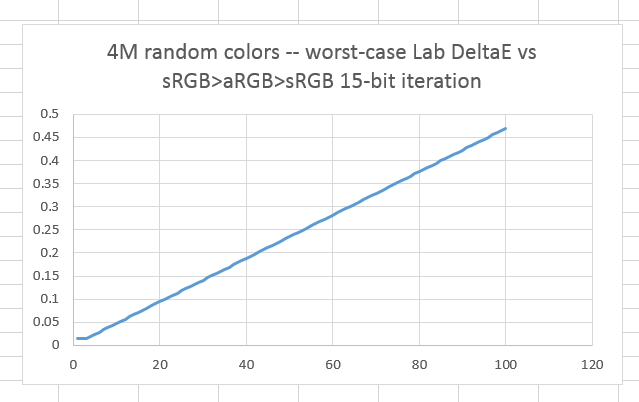
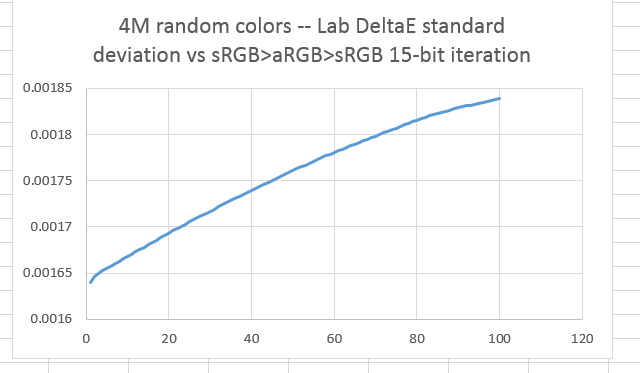
Some say that Photoshop only has 15 bits of precision in its working color space. If we redo the tests with the post-conversion quantizing set to 15 bits, we get worst case numbers like this:
And standard deviations like this:
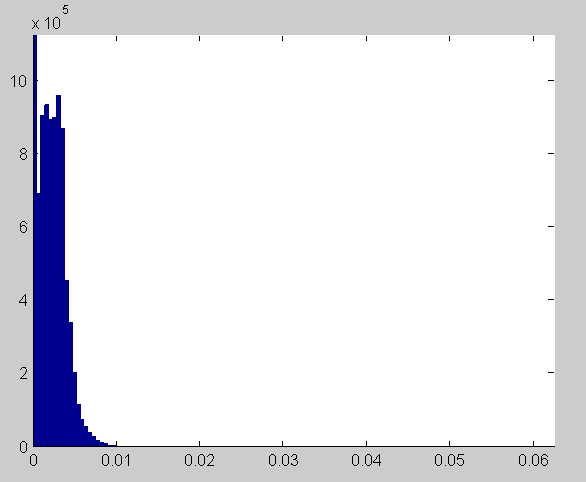
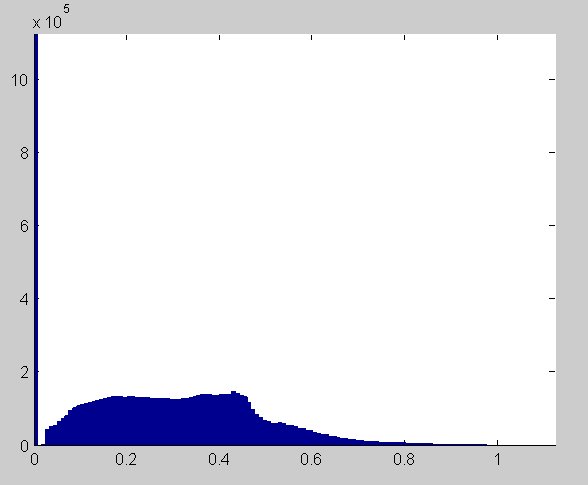
The DeltaE histogram after 100 iterations is as follows (note that the top is chopped off for clarity):
With 15 bit precision, everything looks twice as bad as it does with 15-bit quantizing, but not bad at all in absolute terms.
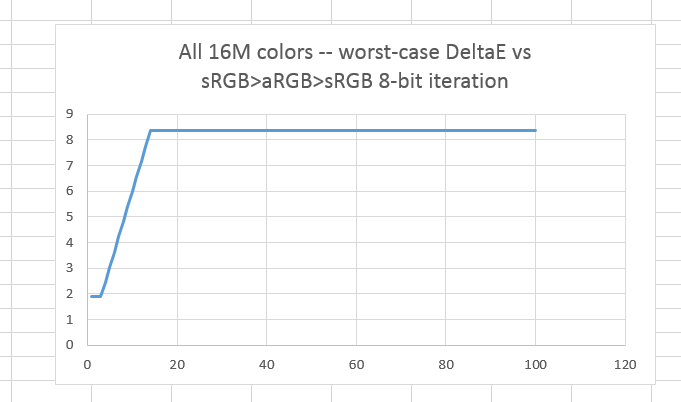
When we look at quantizing to 8 bits, we no longer need a random color image; we can use an image with all 16 million colors representable with 8-bit precision. Repeated round trip conversions at 8-bit precision results in these worst-case errors:
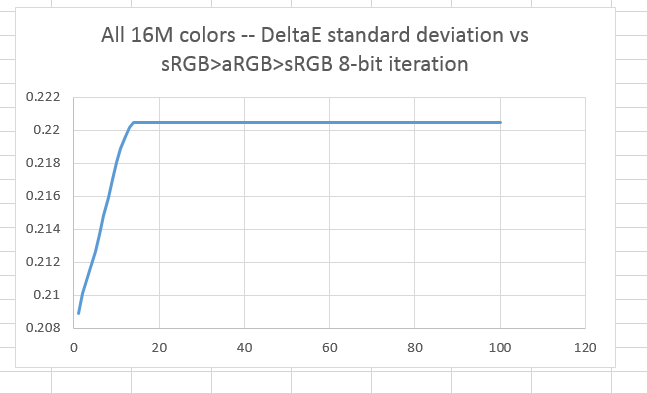
And this is what the standard deviation looks like:
The worst-case errors are considerable with 8-bit precision, but after less than 20 iterations, they stop getting worse. This is cold comfort, because in reality you’d be editing the image with each iteration, creating new colors to be lightly mangled by the conversion.
After 100 iterations, the histogram looks oddly lumpy:
Leave a Reply