Is the Otus diffraction limited?

With a lens this good, the real question is. “At what f-stops is the lens diffraction-limited.?” I thought I’d try to find out. The motivation is to get some insight into how close real photographic lenses are to being diffraction-limited, and thus learn whether or not the concept of Imaging System Q, which I’ve been talking about in the last few posts, applies to normal photography, and not just aerial and orbiting cameras.

I mounted the Zeiss 55mm f/1.4 Distagon ZF.2 (hereafter called the Otus) to the Sony alpha 7R. I mounted a RRS L-plate, clipped it in landscape orientation into an Arca Swiss C1 head which was attached to a set of RRS TVC-44 legs.

I lit an Imatest SFRPlus target with a Paul Buff Einstein strobe. I set the ISO to 100, the shutter speed to 1/10 second, programmed second curtain synch to deal with any shutter vibrations, focused wide open, and set the aperture to f/11. Using the variable power output on the Einstein to control the light level, I made a series of ten exposures each at f/11, f/8, f/5.6, f/4, and f/2.8. I developed the images in Lightroom 5.4 with sharpening and noise reduction turned off, exported them as TIFFs, and measured on-axis MTF50 and MTF30.

Here’s what I got, including confidence lines two standard deviations above and below the averages:

Well, we know that the Otus’ best f-stop for on-axis performance is f/5.6, and that it doesn’t fall off very fast on both sides of that. But what do we know about where it’s diffraction-limited? Not much.

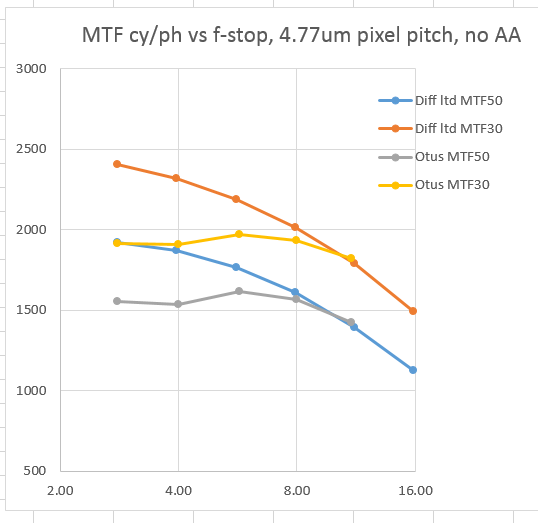
I turned to my camera simulator, and programmed it to model a camera with the same pixel pitch as the a7R (and, as it happens, as the Nikon D800E), no AA filter, and 550 nm illumination. I analyzed the simulated images with Imatest, and here are the results plotted on the same graph as the a7R/Otus results:

It looks like the combination is essentially diffraction-limited at f/11 (and presumably f/16), and pretty close to that at f/8.

So the idea of using Imaging System Q on normal (well, very good) cameras and lenses isn’t so far-fetched.

There’s another lesson here. Notice that the MTF keeps going up as the perfect lens is opened up. Sure, a 4.77 micrometer pixel pitch isn’t enough to get anywhere near what the ideal lens can deliver at those wide openings, but it still helps to have a sharper image falling on the sensor.

It’s the flip side of what we saw when we were investigating the benefits of higher sensel density. It helps, and it continues to help past the point where the sensor’s contribution to the MTF falloff is not as important as the lens’s.

More to come.