Same test image as yesterday 4000×4000 monochromatic, 16-bit gray gamma 2.2, filled with a constant signal of half-scale, (0.5, 127.5, or 32767.5, depending on how you think of it), with Gaussian noise with standard deviation of 1/10 scale added to it. The image was created in Matlab, written out as a 16-bit TIFF, read into Photoshop, downsized by various amounts using Bicubic Sharper interpolation, exported as a 16-bit TIFF, read back into Matlab, and analyzed there.
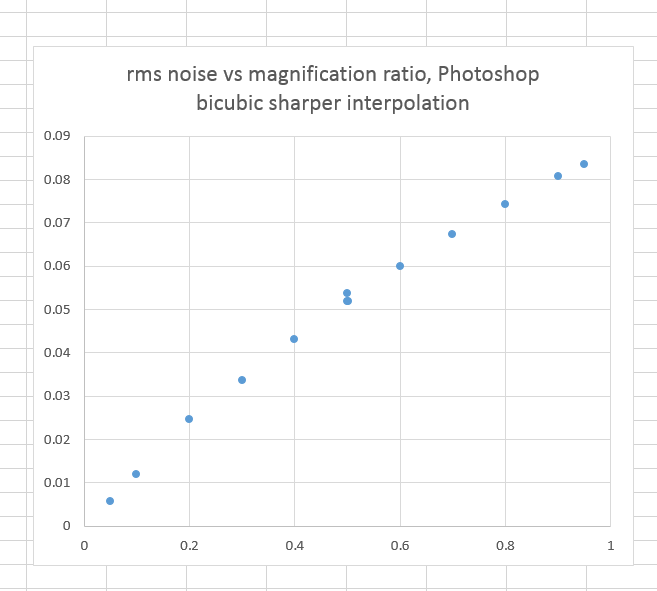
RMS noise, aka standard deviation, of the downsampled images as measured in gray gamma 2.2:
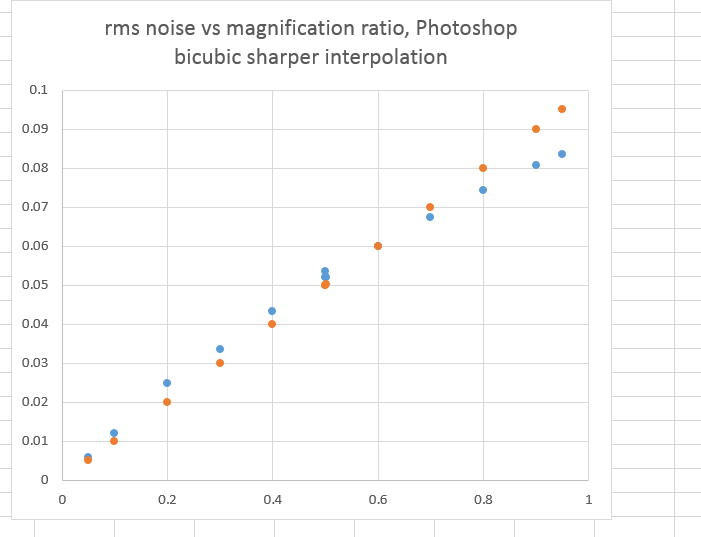
As in the case of bilinear interpolation, the Photoshop results are dramatically different than the Matlab ones; in this case the standard of comparison that I’m using in Matlab is simple bicubic, since there is no algorithm for imresize called “bicubic sharper”, If you look at it with a set of orange dots indicating “perfect” results, you can see we’re pretty close:
A little worse at low reduction ratios, a little better from 1/8 to 1/2. There’s a strange anomaly around 1/2 — both 0.501 and 0.499 have slightly less noise than 0.500 — but that’s hardly worth worrying about, since a look at the spectra of all three indicate that they’re very similar.
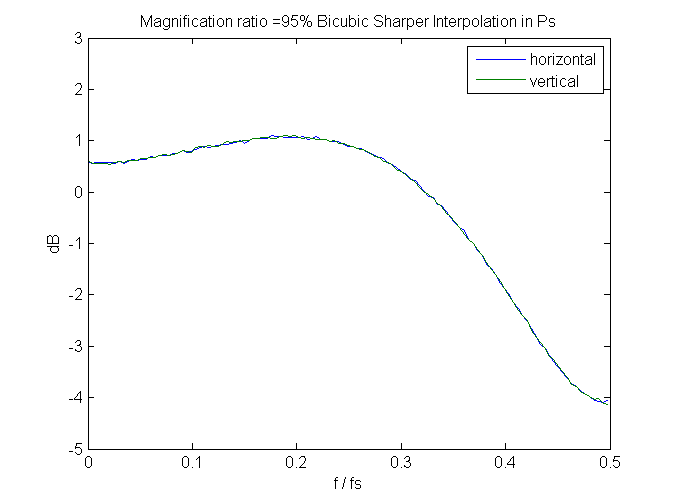
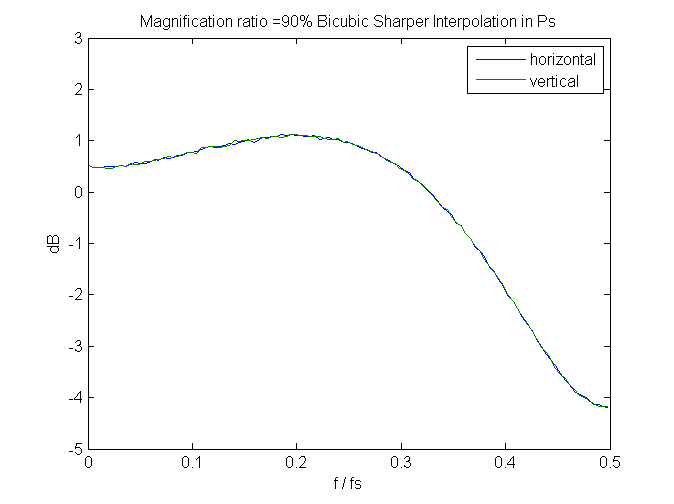
And, speaking of spectra, if we look at a few, we can see that bicubic sharper gets its exemplary noise reduction properties by attenuating the highest spacial frequency signals. It needs to do something there, since it boosts signals slightly below those.
Since these are measured in the frequency domain of the output image, perfect behavior would be that the spectra don’t change with magnification. We don’t get that; greater downsampling (lower magnification) results in higher peaks and sharper cuts. Still, it’s not bad, if you don’t mind giving up that last octave of sharpness.
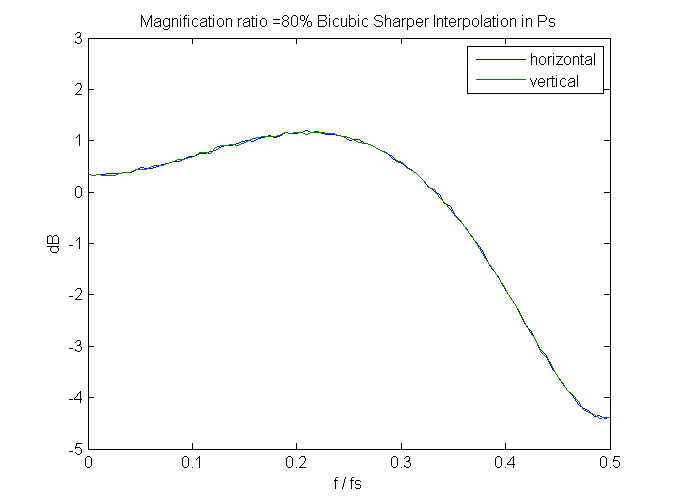
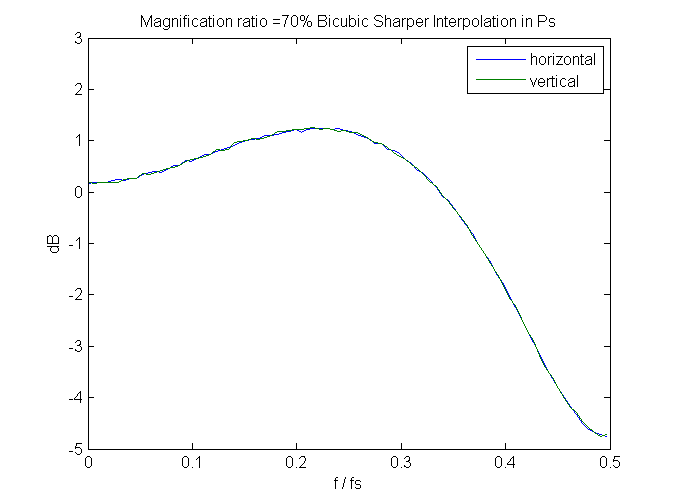
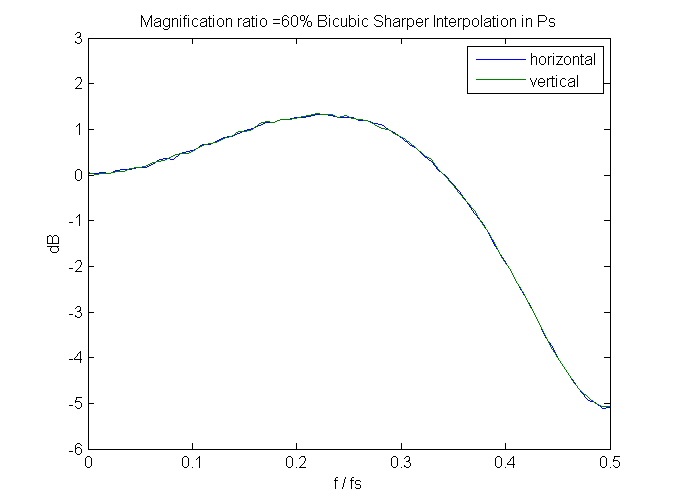
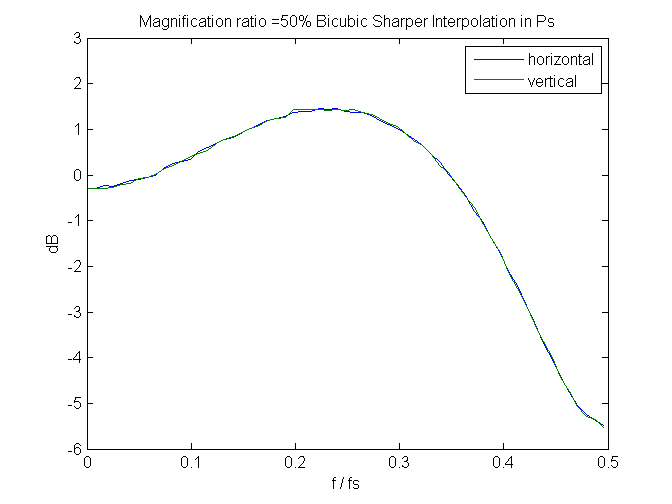
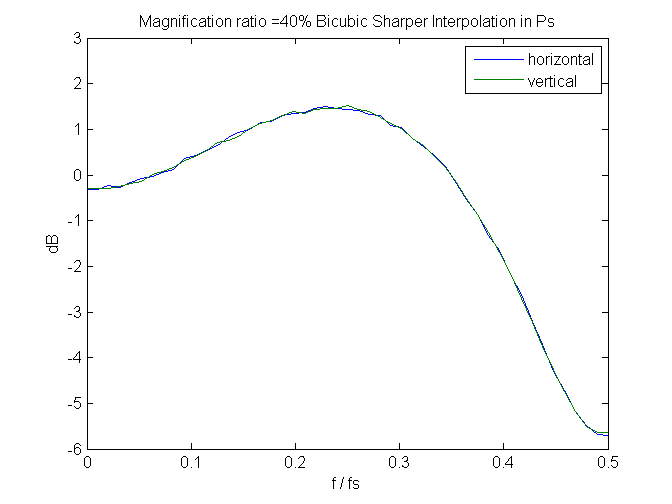
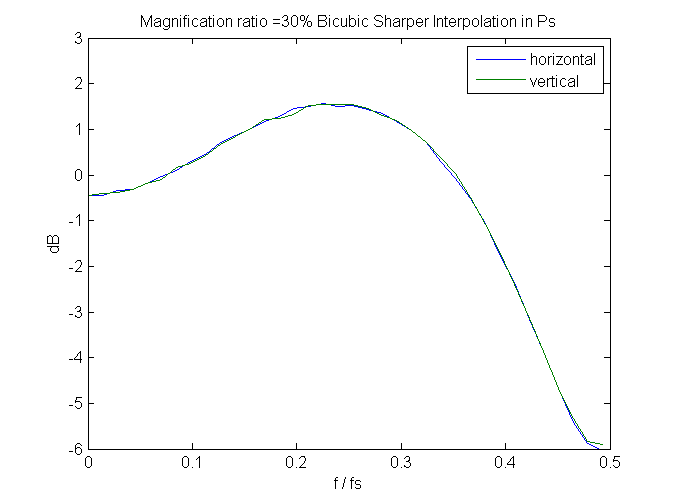
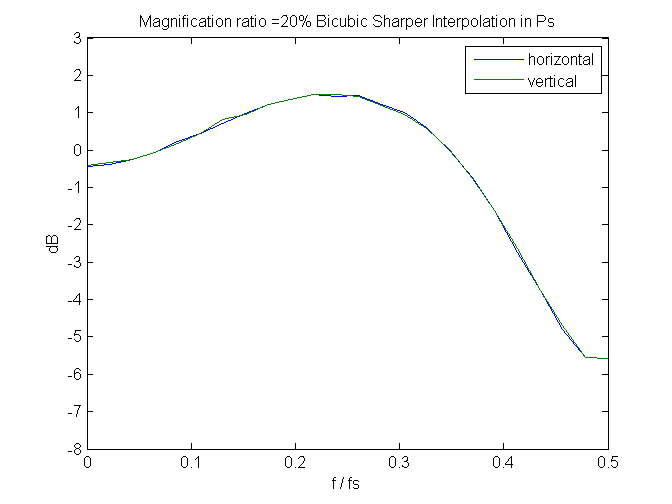
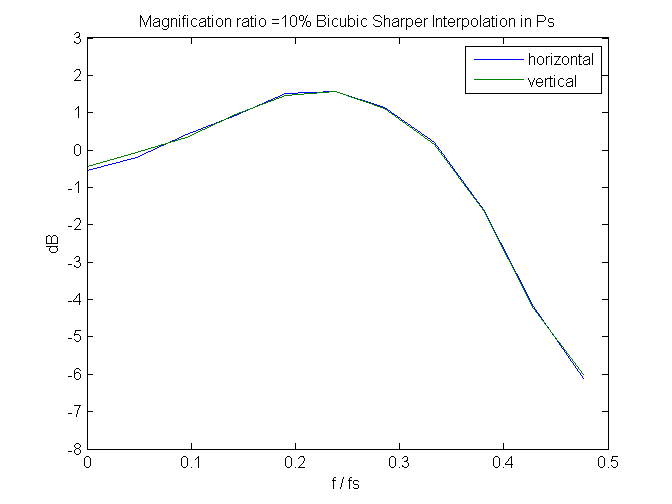
Leave a Reply