When I last left you, the jury was out on the issue of whether the bilinear interpolation downsizing algorithm in Photoshop was the same as the one in Matlab. The jury is back.
“Mr. Foreman, have the jury reached a verdict?”
“We have, your honor.”
“May I hear it?”
“The algorithms are wildly different, as indicated by the spectra and rms value of downsampled noise images.”
“I thank and excuse you all.”
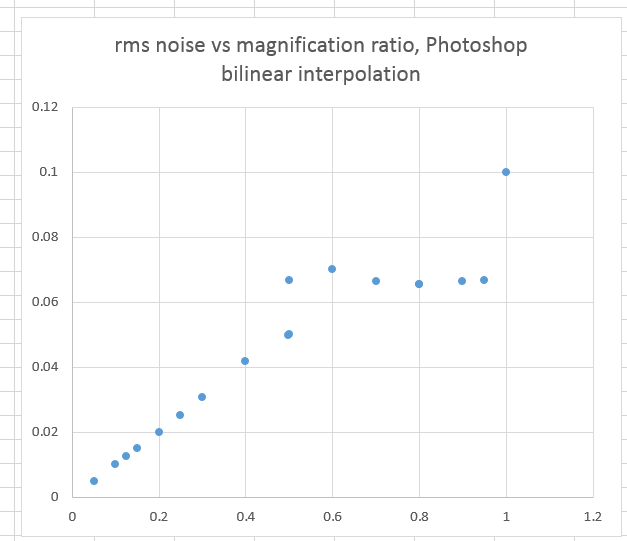
Here’s a graph that says a lot (the noise was measured in a space with the same nonlinearity as it the one in which it was originally generated):
There’s good news; below 50%, the noise is pretty much in line with where photographic equivalency says it should be. At ratios near 100%, there’s less noise than we’d think, and at numbers between 50.1% and about 75%, there’s more noise than we’d think.
There is a discontinuity in the curve at 50%. I’ve plotted noise measurements for 49.9%, 50%, and 50.1% magnification. 50% and 49.9% are just about on top of one another, but 50.1% is substantially noisier.
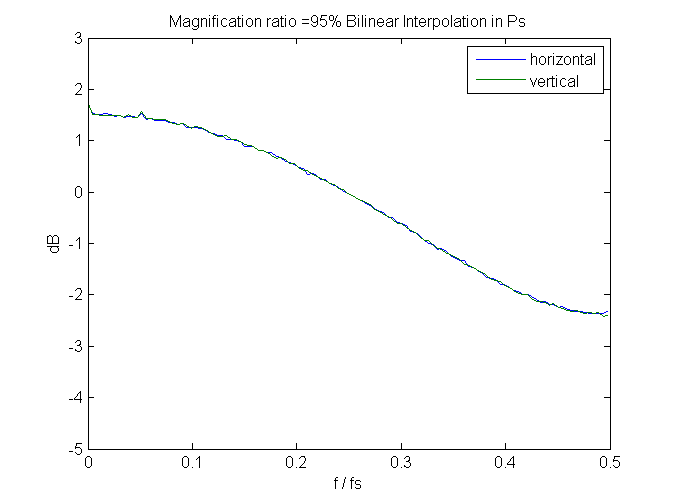
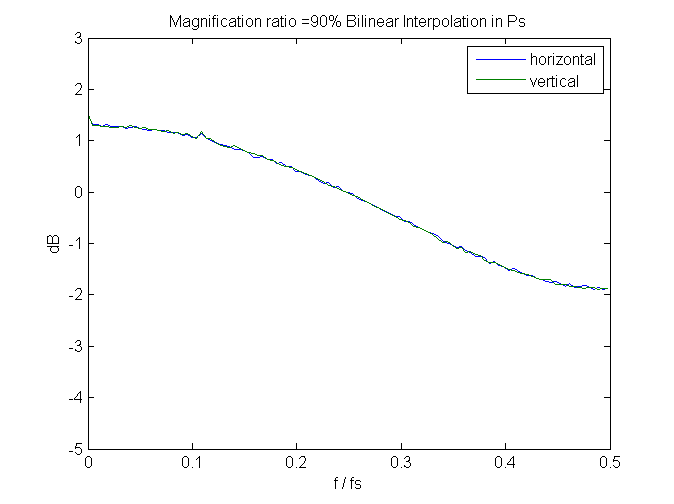
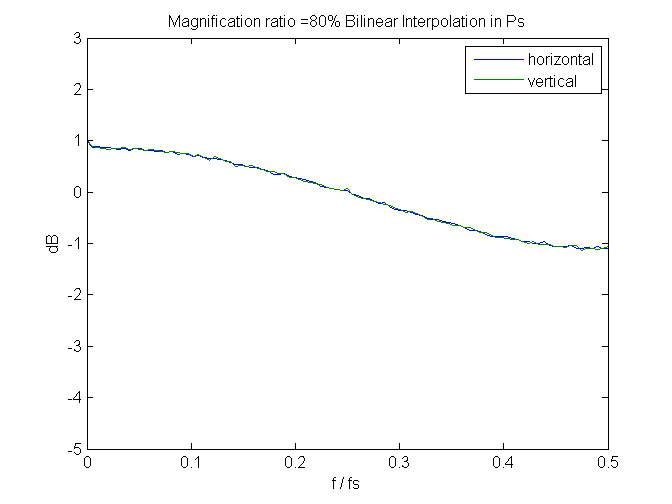
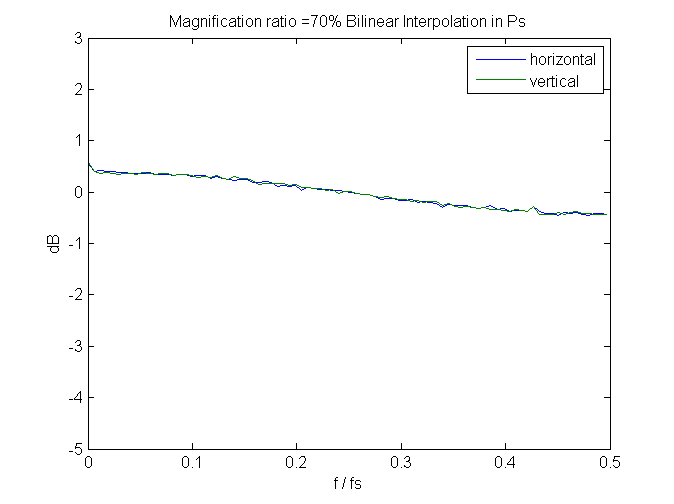
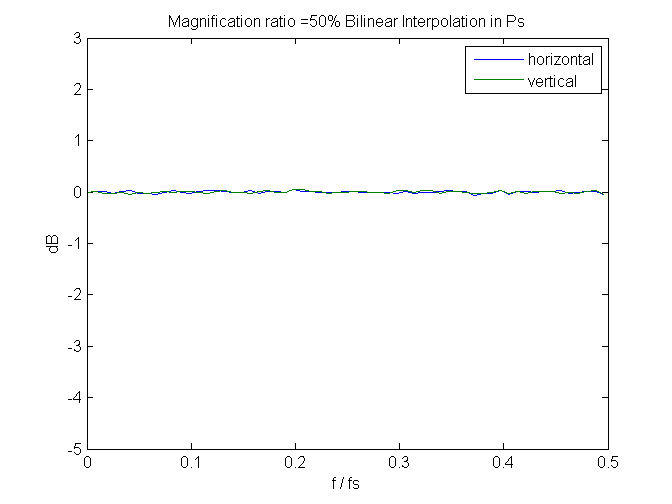
We can learn something by looking at the spectra of some of the images.
There’s quite a bit of high frequency rolloff at 95% magnification:
Less at 90%:
Less at 80%:
Hardly any at 70%:
And flat at 50%:
The curves stay flat below that.
From the rms noise and spectral curves, it appears that neither Matlab nor Photoshop are just picking the four points in the input image nearest to the required point in the output image, Matlab seems to do that if power-of-two reduction ratios aren’t used, but also seems to ignore points in the input image that are right over points in the output image. If they didn’t, for reduction ratios that consisted entirely of those points, there would be no noise reduction at all.
What’s Photoshop doing? Anybody who knows, please sing out. I’m sure they’re not lying when they say they are using bilinear interpolation, but, from the low noise at high reduction ratios, they’re using a lot more than four points at those ratios.
Next up: Photoshop’s Bicubic Sharper.
The trouble with regarding pixels as points rather than rectangles, and considering only the four source points nearest to the destination point, is that it throws away a lot of information. At a scale of 0.2 you’re discarding 21 pixels worth of information, averaging the values of just four pixels, which limits the amount of noise reduction that can occur.
The other interpretation of bilinear scaling is of a 1×1 pixel window moving across the original image, calculating the average of the four rectangular pixels it partially covers, weighted by the area of each pixel that it covers, sampled at the centre of each pixel in the new image.
In order to avoid throwing away data, you could modify the algorithm for down-scaling by increasing the size of that window to the size of the pixels in the new image and calculating the weighted average of all the original image pixels it wholly or partially covers.
The alternative would be to apply a blur function to the original image, with the radius linked to the scaling factor, ensuring that when you proceed with standard bilinear scaling, the four source pixels you base your new pixel value on are already partially averaged with the pixels around them.
I suspect PS is using one of those approaches. Either one should reduce the noise in line with what photographic equivalency suggests.
I’m not proficient in Matlab, but I’d expect these approaches to be pretty simple to implement – the big question would be, in the second version, exactly what blur function to use, and what parameters to use for a given scaling factor.
That makes sense.
I’ve already done some downscaling work in Matlab using pre-blur (AA) filters. Look back a couple of posts. It would be useful to know exactly how Ps does this (if indeed this is what it does) with bilinear and bicubic sharper, so I could implement the same algorithms in Malab. Trying to reverse engineer it might take a long time, and I could still be wrong.
As to the simplicity of implementation of the above approach, it should be pretty easy; imresize allows user-supplied kernels.
If the window size is increased, I’d need the details of that to code up a Matlab implementation that worked the same way.
Jim