Chained color space conversion errors with many rgb color spaces

[Note: this post has been extensively rewritten to correct erroneous results that arose from not performing adequate gamut-mapping operations to make sure the test image was representable within the gamut of all the tested working spaces.]

I’ve been trying to come up with a really tough test for color space conversion testing, one that, if passed at some editing bit depth, would give us confidence that we could freely perform color space conversions to and from just about any RGB color space without worrying about loss of accuracy. I think I’ve  found such a test.

I picked 14 RGB color spaces that, in the past, some have recommended as working spaces, although several of them are obsolete as such:

1. IEC 61966-2-1:1999 sRGB
2. Adobe (1998) RGB
3. ProPhoto RGB
4. Joe Holmes’ Ektaspace PS5
5. SMPTE-C RGB
6. ColorMatch RGB
7. Don-4 RGB
8. Wide Gamut RGB
9. PAL/SECAM RGB
10. CIE RGB
11. Bruce RGB
12. Beta RGB
13. ECI RGB v2
14. NTSC RGB

If you’re curious about the details of any of these, go to Bruce LIndbloom’s RGB color space page and get filled in.

I wrote a Matlab script that reads in an image, assigns the sRGB profile to it, then computes from it an image that lies within all of the above color spaces. It does that with this little bit of code:

This script didn’t pull the gamut in far enough that the buildup of double precision floating point round-off errors didn’t cause colors to be generated that were out of the gamut of some of the color spaces. I added another gamut-shrinking step:

This code shrinks the gamut somewhat in CIELab. I could probably get away with less shrinkage, but I got tired of watching the program go through many iterations before it finally threw a color out of gamut, forcing me to start all over again.

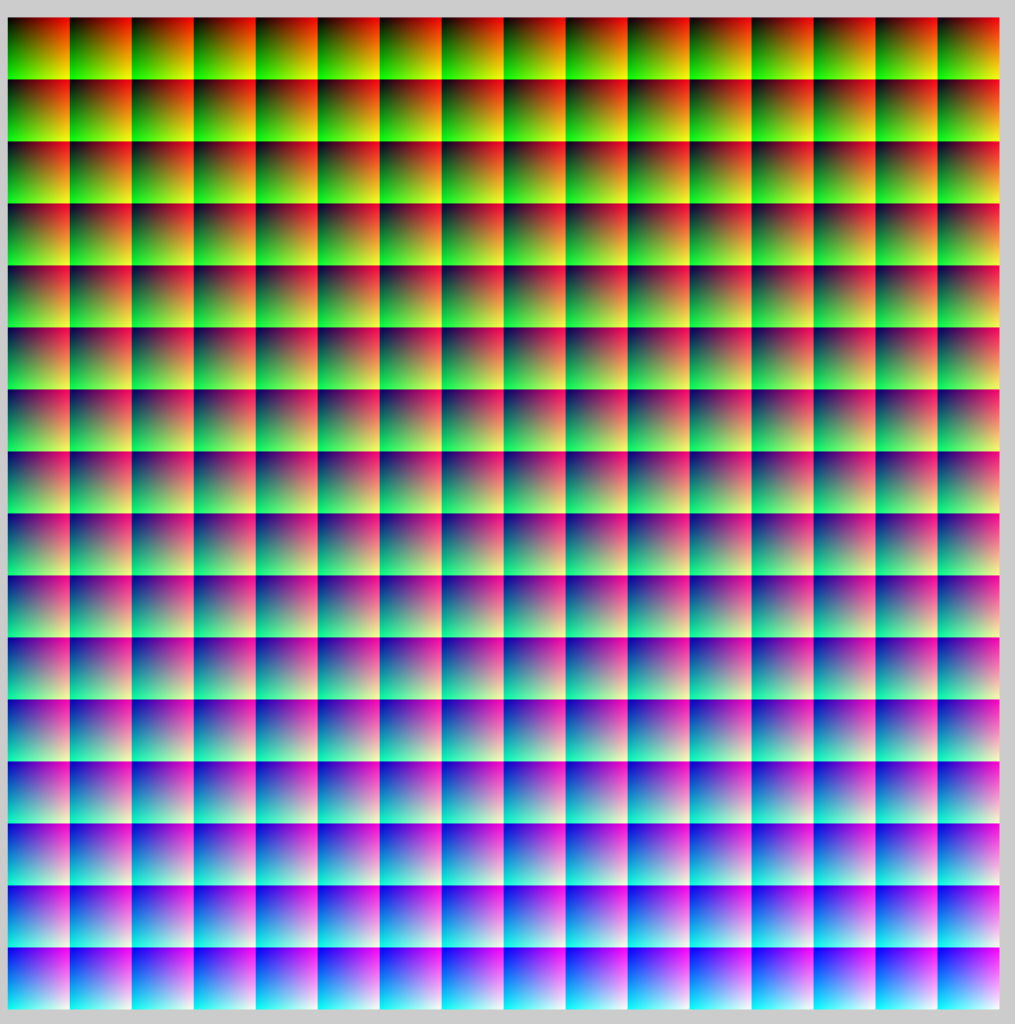
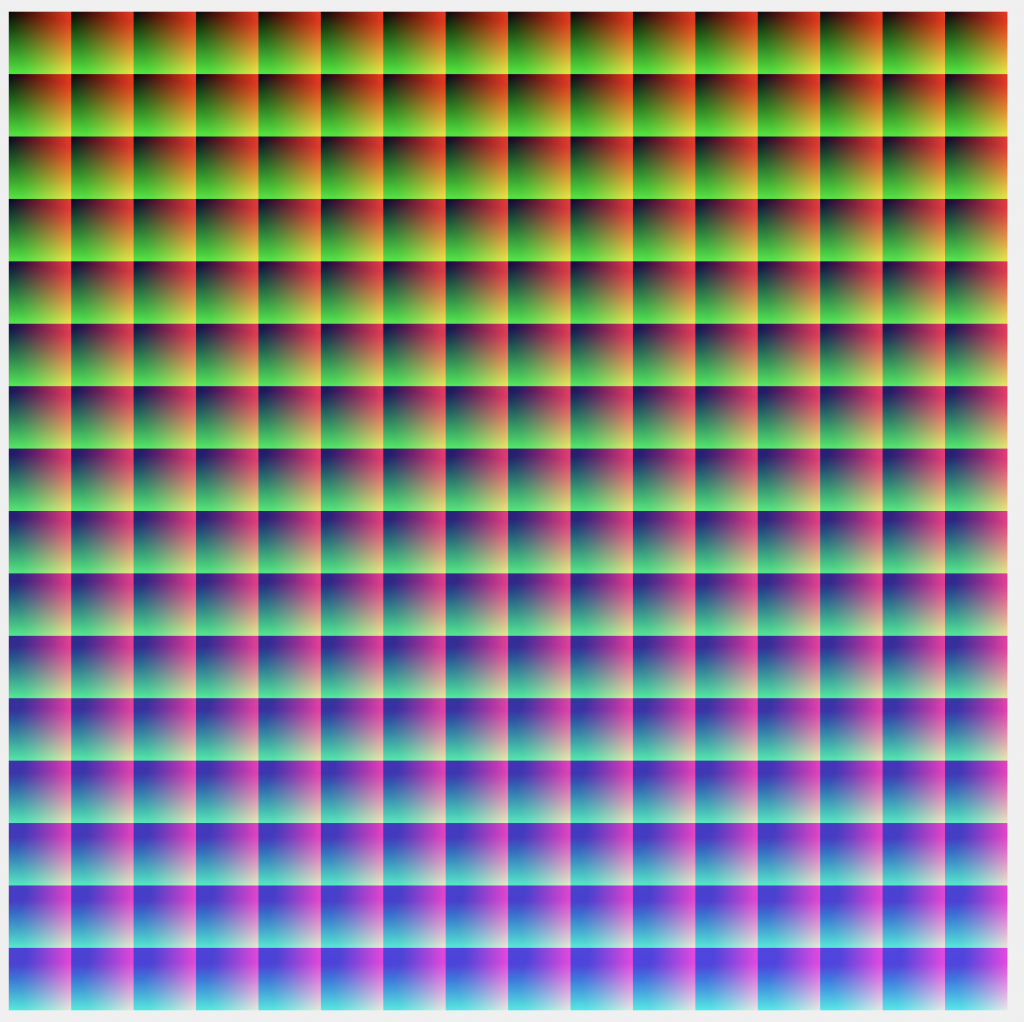
Here’s the sRBG image before the gamut-constraining process:

And here it is afterwards:

Here’s the difference between the two in CIELab DeltaE, normalized to the worst-case error, which is about 45 DeltaE, and a gamma of 2.2 applied:

After the gamut-constraining, the program picks a color space at random, converts the image to that color space algorithmically (no tables) in double precision floating point, quantizes it to whatever precision is specified, measures the CIELab and CIELuv DeltaE from the original image, then does the whole thing again and again until either the computer gets exhausted or the operator gets bored.

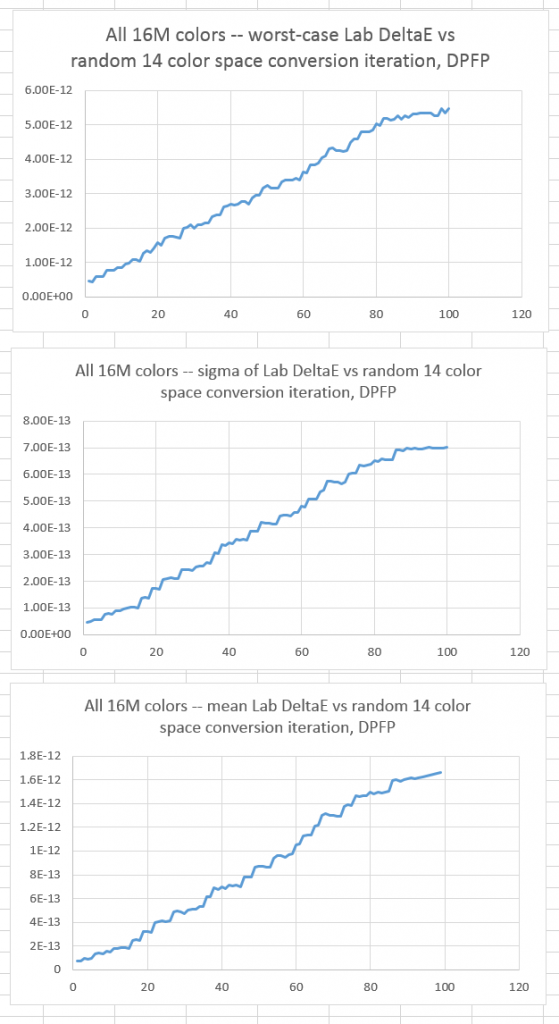
Here’s what happens when you leave the converted images in double precision floating point:

The worst of the worst is around 5 trillionths of a DeltaE.

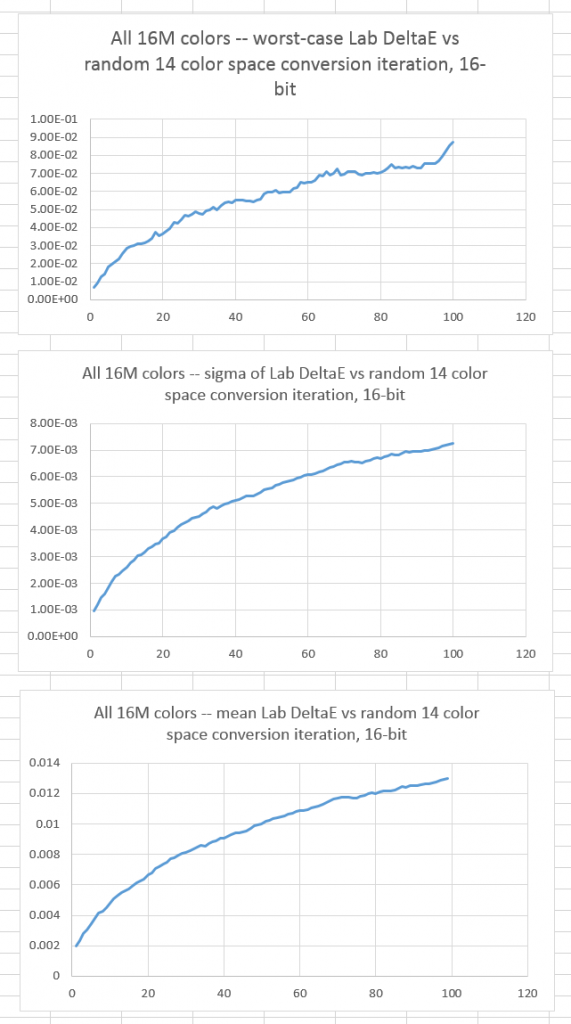
If we quantize to 16 bit integers after every conversion:

The worst case error is less than a tenth of a DeltaE, and the mean error is a little over 1/100th of a DeltaE.

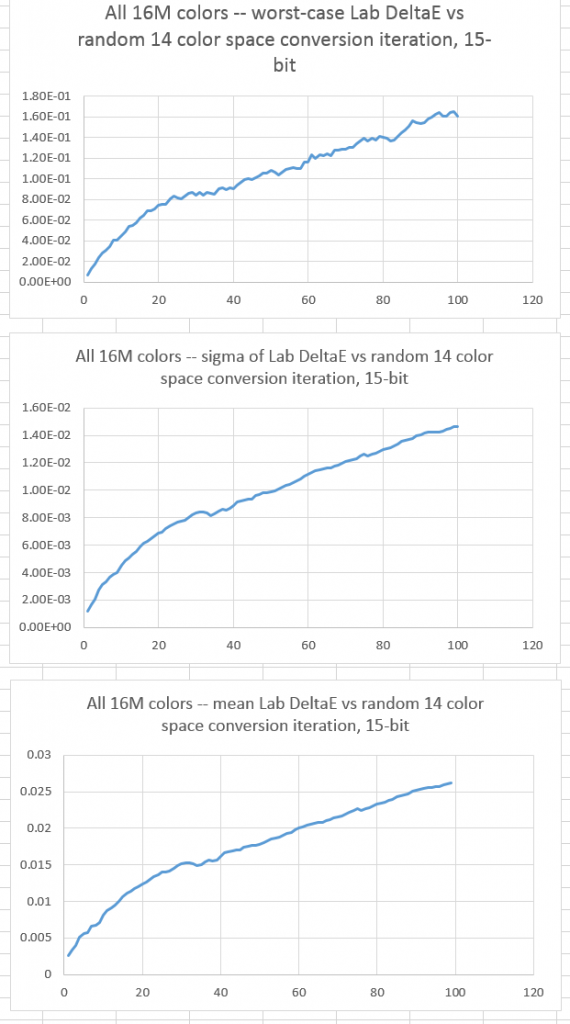
With 15-bit quantization, here is the situation:

More or less the same as with 16-bit quantization, but the errors are twice as bad. The worst-case error doesn’t get over one DeltaE until about 40 conversions, though.

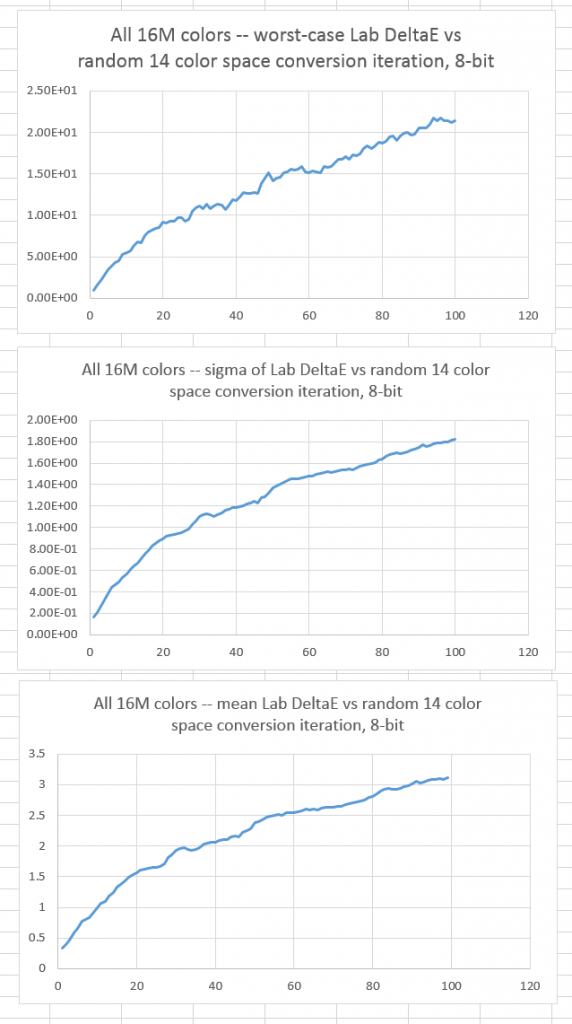
With 8-bit quantization, we see a different story, as the quantization errors dominate the conversion errors get obvious quickly: