Sequential color space conversions at varying precision

I am now spreading my color space net to include a wide variety of possible RGB working color spaces. I picked 13 for testing:

1. IEC 61966-2-1:1999 sRGB
2. Adobe (1998) RGB
3. Beta RGB
4. Bruce RGB
5. CIE RGB
6. ColorMatch RGB
7. Don-4 RGB
8. ECI RGB v2
9. Joe Holmes’ Ektaspace PS5
10. PAL/SECAM RGB
11. ProPhoto RGB
12. SMPTE-C RGB
13. Wide Gamut RGB

If you’re curious about the details of any of these, go to Bruce LIndbloom’s RGB color space page and get filled in.

I wrote a program to take an image of all 16+ million possible colors in SRGB and map it into an sRGB image that is within the gamut of all of the above color spaces. More on how I did that in a subsequent post.

Then I wrote a program to convert the image to sRGB, the first on on the above list, and convert that image to all the other color spaces on the above list in list order. Then it moved on to the next color on the list, and did the same thing again. And again, and again, until it reached the bottom of the list. It skipped the conversions to the source color space. That gave me 13*12, or 156 conversions. I set up the program so that it would either leave the image in double-precision floating point after the conversions, or quantize it to integers whose precision I could choose. Then I computed some stats.

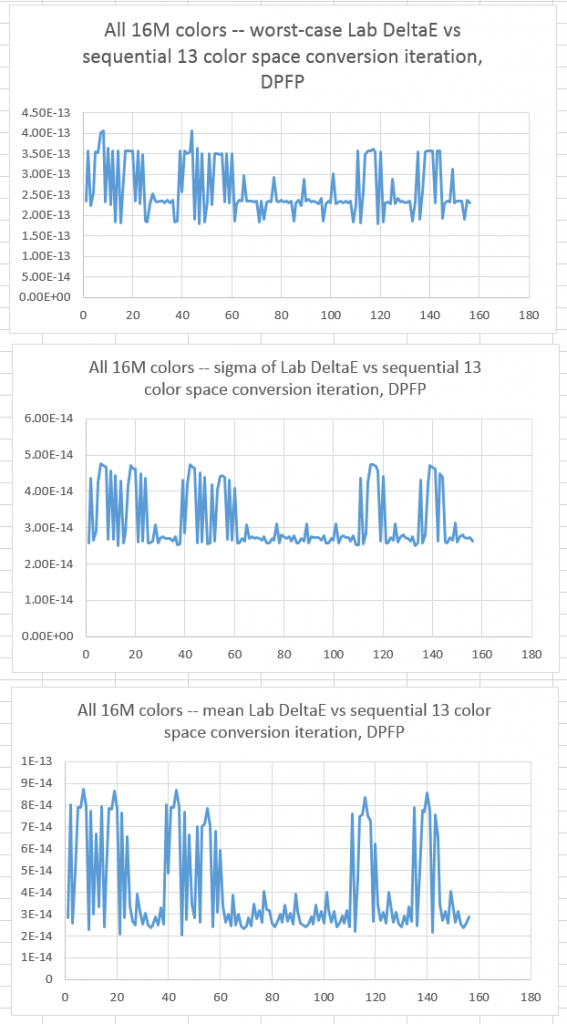
Here’s the result of leaving the converted images in 64-bit floating point:

Some conversions produce greater errors than others, but all the errors are very small, being much less than one-trillionth of a DeltaE

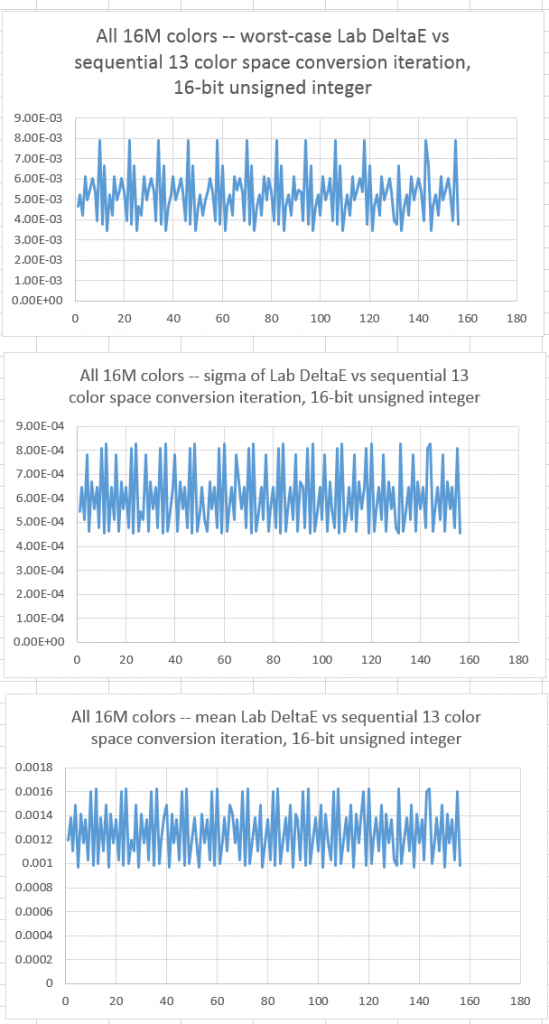
If we convert each image to 16-bit unsigned integer representation after each conversion, we get this:

The errors are all under one-thousandth of a CIELab DeltaE.

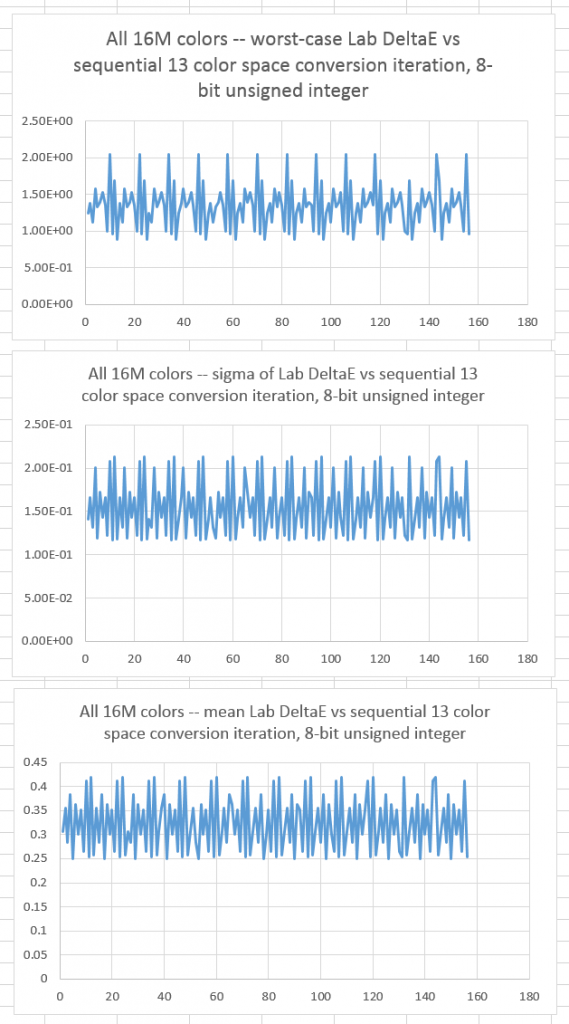
With conversion to 8-bit unsigned integer representation after each conversion:

Now we have mean errors of 1/3 of a DeltaE, and worst-case errors of about 2 DeltaE. You definitely want to be careful when converting color spaces if you’re working with 8-bit images.

I expected that some RGB color space conversions would be more prone to error than others, and that turns out to be the case. What surprises me is how small the differences are — one binary order of magnitude covers them all.