This is the third post on balancing real and fake detail in digital images. The series starts here.
In the last post, in this series, I showed you some plots of a real sharpness metric and an aliasing metric versus f-stop for an ideal diffraction-limited lens and a camera with a 3.76 micrometer pixel pitch and a 100% fill factor. To tie this mathematical exercise to the real world, both the Fuji GFX 100 and the Sony a7RIV materially fit that description. Those graphs has two measures, and humans, including this one, are biased to seek scalars. You lose a lot when you go from a vector to a scalar space, and the issue of how to weight the dimensions of the vector is infinitely malleable, but I thought I’d give it a whack here.
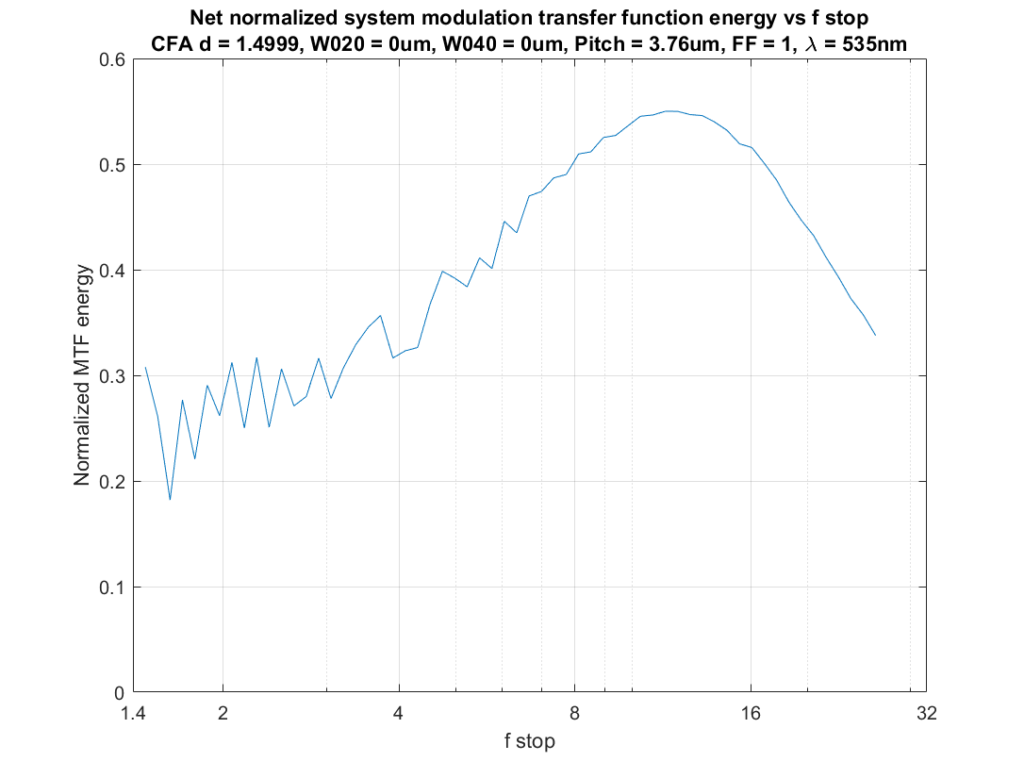
My proposed metric is simply the normalized amount of energy below Nyquist (which results in accurate reconstruction) minus the (same normalization) amount of energy above Nyquist, which results in bogus (in this case, at least, bogus is a technical term for erroneous) reconstruction.
Here’s what that looks like for our diffraction-limited lens, with a Bayer-CFA Nyquist frequency divisor of 1.5:
The sweet spot is between f/8 and f/16. That seems like a long way to stop down. Here are some reasons why you might be able to get away with a wider aperture:
- Your subject doesn’t have a ton of high-frequency detail
- Your focusing isn’t perfect
- Your subject is three dimensional
- Your lens isn’t diffraction limited
- You and your viewers don’t notice aliased detail much
- You and your viewers actually like the crisp look that aliasing provides
Erik Kaffehr says
Jim,
It could be interesting if you have rerun some of your calculations with OLP filter.
I would also much thank you for sharing your knowledge and experience in so many fields related to photography.
Best regards
Erik
FredD says
Jim, I appreciate your attempt in this series to relate the results predicted to your experience at specific f-stops, (which does certainly validate your analysis as ballpark-correct, at least at these specific pixel sizes), and you do here have a list of caveats. But I couldn’t help but remember an old analysis by Kjell Carlsson of the pinhole camera:
The Pinhole Camera Revisited
or
The Revenge of the Simple-Minded Engineer
https://www.kth.se/social/files/542d2d2df276546ca71dffaa/Pinhole.pdf
My point is that the above reminds that not only area under the mtf curve (or parts thereof) but also its shape can be very important in perceived quality. Might apply not only to resolution but also moire analysis.
So perhaps desirable to weight the mtf values by applying some transformation function that emphasizes human visual system response?
That said, I’m probably being too picky, and your analysis is much appreciated.
JimK says
Like Ed Granger’s SQF?
http://www.imatest.com/docs/sqf/
That requires specifying a print size and viewing distance.
FredD says
Yes, possibly SQF (though I’m not familiar with alternate ones, so I’d be hard-pressed to know what would be best).
And while SQF would be at specific print sizes (and distances), once those were decided upon it’s not that difficult in presentation, as a color-coded chart for that was standard at Popular Photography for many years.
JimK says
I’m not eager to write that code.