This is a continuation of a report on new ways to look at depth of field. The series starts here:
For the past few posts, I’ve been developing the concept of a hyperfocal distance based on the allowable degradation of image resolution as measured by MTF50. There are two convenient properties of hyperfocal distance as calculated using the conventional circle of confusion (CoC) methods.
- If you focus the lens at infinity, the allowable near limit of sharpness occurs at the hyperfocal distance.
- If you focus the lens at the hyperfocal distance, the allowable near limit of sharpness occurs at half the hyperfocal distance.
Wouldn’t it be nice if both those things applied to the new MTF50-based hyperfocal distance? It turns out they do, perhaps not exactly, but darned close.
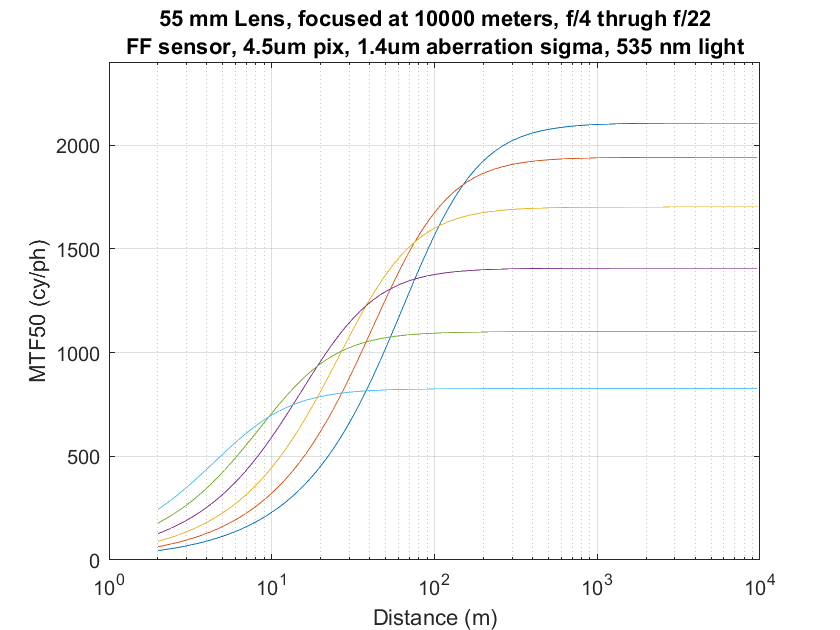
If we focus our top-notch 55 mm lens at almost infinity, here’s what we get:
Now, let’s say that we want the hyperfocal distance (HFD) for 90% of the resolution available at infinity when the lens is focused there. If, for each aperture, we drop down on the right side of the graphs to 90% of the MTF50 value where the line hits the end of the graph, and trace that value back to the left on the graph until we encounter the line for that aperture, we get the hyperfocal distance for that sharpness tolerance and aperture.
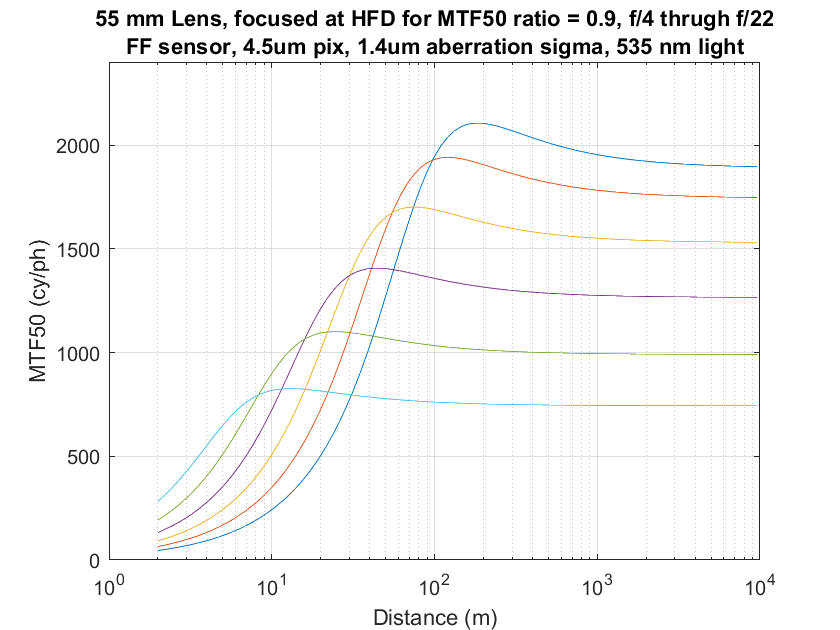
If we run a set of curves with the lens focused to those hyperfocal distances, we get this:
The peaks are at the hyperfocal distances for each stop (no surprise there; that’s where we focused the lens). The amount of sharpness reduction at infinity in each case is the reduction we saw when we graphically found the HFDs. You’re going to have to trust me on this last one, since the distance scale is compressed, but the place where the sharpness nearer than the HFD falls to the value at infinity is half of the HFD.
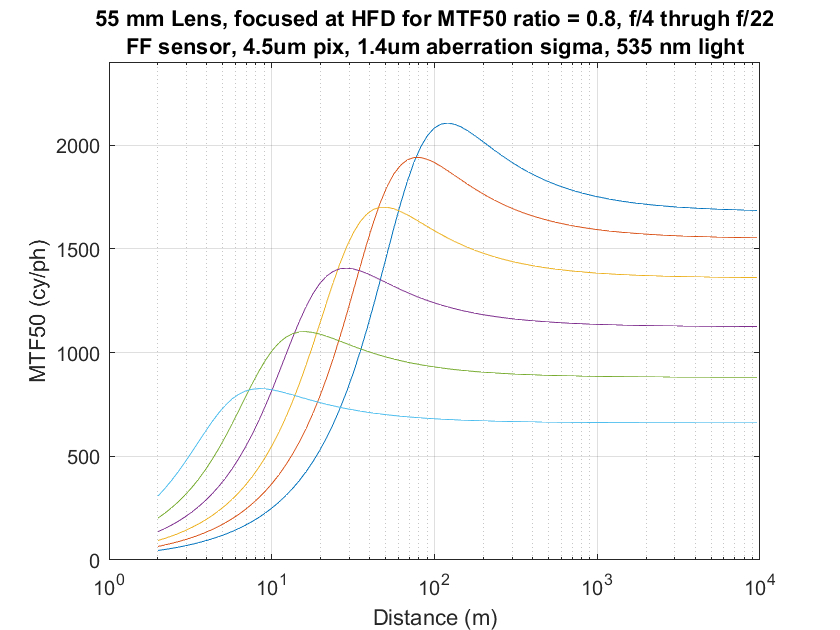
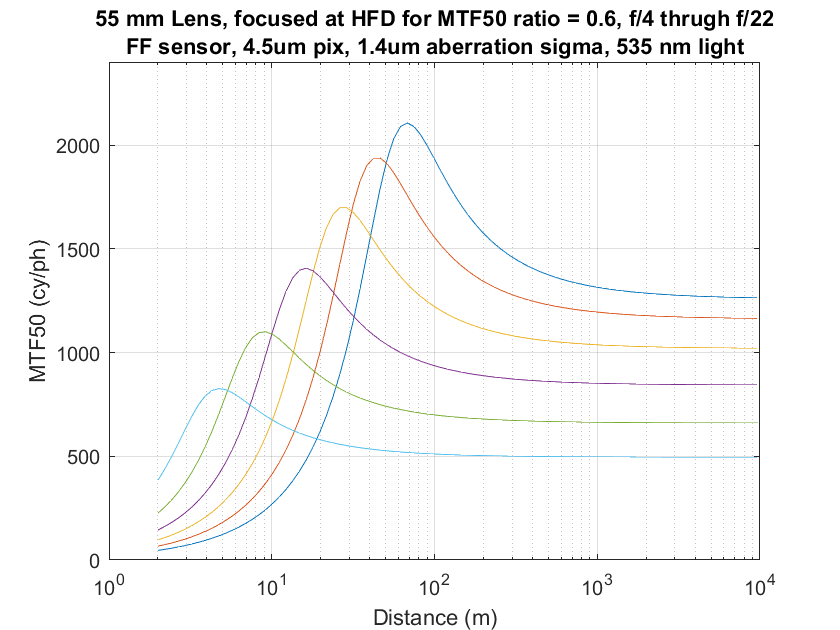
Here are two more graphs for lower tolerance ratios:
The same thing happens. I’m not sure exactly why this is true, but it’s very convenient. [Edit: The surprise to me was that relationship survives even after all the additional sources of blurring other than defocus. Thinking about it now, it makes sense, since the model for all those is that they are insensitive to defocusing, and thus affect the near and the far points equally.]
So the real relation would be that the sharpness at infinity is equal to sharpness at 1/2 the focus distance, regardless of whether or not you’ve done hyperfocal distance or gone for the bokeh.
And that makes sense, actually. In image space, they’re roughly the same distance away from the focal point, so they’ll be blurred equally (as a first order approximation).
Thin lens equation: 1/s1 + 1/s2 = 1/f
When f = 50mm and s1 is 5000 mm, you get s2 = 50.5050…mm.
When f = 50mm and s1 is 2500 mm, you get s2 = 51.0204…mm.
When f = 50mm and s1 is infinity, you get s2 = 50mm.
They’re about equidistant from the focal plane.
Right. The surprise to me was that relationship survives even after all the additional sources of blurring other than defocus. Thinking about it now, it makes sense, since the model for all those is that they are insensitive to defocusing, and thus affect the near and the far points equally. I think I’ll go back and add that.
Jim