In the last half-dozen posts, I’ve explored the noise reduction effects and quality of the results from six or seven different downsampling methods. From doing that work, I’ve concluded that there are several choices for someone with a small-pixel camera to produce images that have similar noise characteristics as those made with a large-pixel camera, after the small-pixel images are down res’d to the resolution of the large-pixel camera, as stated by photographic equivalence.
The above depends on the FWC of the cameras being proportional to the square of the pixel pitch. It further depends on an assumption about read noise. If the read noise of the cameras involved is proportional to the pixel area, then the sun and moon align and the noise part of equivalence is handled.
But the above assumption about read noise is suspect. I’ll make one that’s pretty far out in the other direction. Let’s assume the read noise is independent of pixel size. That gives a real advantage to the large pixel cameras. Is it enough for them to win the noise battle with their small-pixel brethren at the same downsampled resolution?
Not if you throw non-linear noise reduction techniques like those baked into Lightroom and Adobe Camera Raw.
Here’s how I know. I used my camera simulator to make two “photographs” of Bruce Lindbloom’s desk, with the sim set to ISO 3200, with a 1.25 micrometer (um) pixel pitch, and a 5 um pixel pitch.
The other important parameters that I used are:
- Simulated Otus 55mm f/1.4 lens
- Aperture: f/5.6
- Bayer CFA with sRGB filter characteristics
- Fill factor = 1.0
- 0.375 pixel phase-shift AA filter
- Diffraction calculated at 450nm for blue plane, 550nm for the green plane, and 650nm for the red plane
- Full well capacity = 1600 electrons per square um
- Read noise sigma = 1.5 electrons
- Bilinear interpolation demosaicing
The first two images have been enlarged 3x using nearest neighbor before being JPEG’d. The second two are enlarged by 9x using the same method.
Here’s the scene as captured by the camera above with the pixel pitch set to 5 um:
And at 1.25 um, processed in Lr with luminance noise reduction set to 100, chroma noise reduction set to 100, and exported at 25% magnification by Lightroom with no sharpening:
Now let’s zoom in:
With the 5 um camera:
And the 1.25 um camera:
Being able to use nonlinear noise reduction on the higher resolution camera is a game-changer. The noise in the lower image is actually lower than that in the upper one. However, there’s much more detail in the lower image. The ugly zipper artifacts from the demosaicing are completely gone.
What if we try to do some nonlinear noise reduction on the image from the big-pixel camera. Here’s one attempt:
We lose sharpness and still can’t get the noise down to where it is in the 1.25 um image. We still have residual zipper artifacts on the bottom of the yellow Macbeth patch. There are color errors on the sides of the gray patches.
And this was after making some assumptions about read noise that stacked the deck in favor of the big-pixel camera.




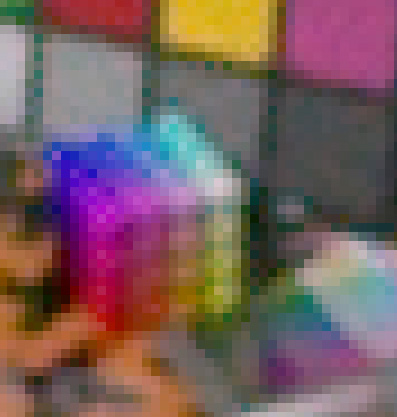
Funny how the noise reduced 1.25um image appears to also have lost contrast and saturation compared to the 5um.