This is one in a series of posts on the Fujifilm GFX 100S. You should be able to find all the posts about that camera in the Category List on the right sidebar, below the Articles widget. There’s a drop-down menu there that you can use to get to all the posts in this series; just look for “GFX 100S”. Since it’s more about the lenses than the camera, I’m also tagging it with the other Fuji GFX tags.
There is a body of opinion that somehow depth of field (DOF) calculators don’t work for GFX cameras. The proponents of that school of thought say that it’s not just a matter of picking the appropriate circle of confusion (CoC) diameter; it’s more fundamental than that. Some of them cite publications by Zeiss that say that the lens aberrations affect the DOF performance of the lens, which is undeniably true, but may or may not be applicable in the case of the GF lenses, which are with some exceptions fairly well corrected.
It occured to me that I have in my current lens-testing protocol a means to measure the actual circles of confusion produced by the GF lenses on the GFX 100S as the subject is defocused, which would allow the actual DOF to be compared to the DOF predicted by geometric optics, upon which depth of field calculators are based.
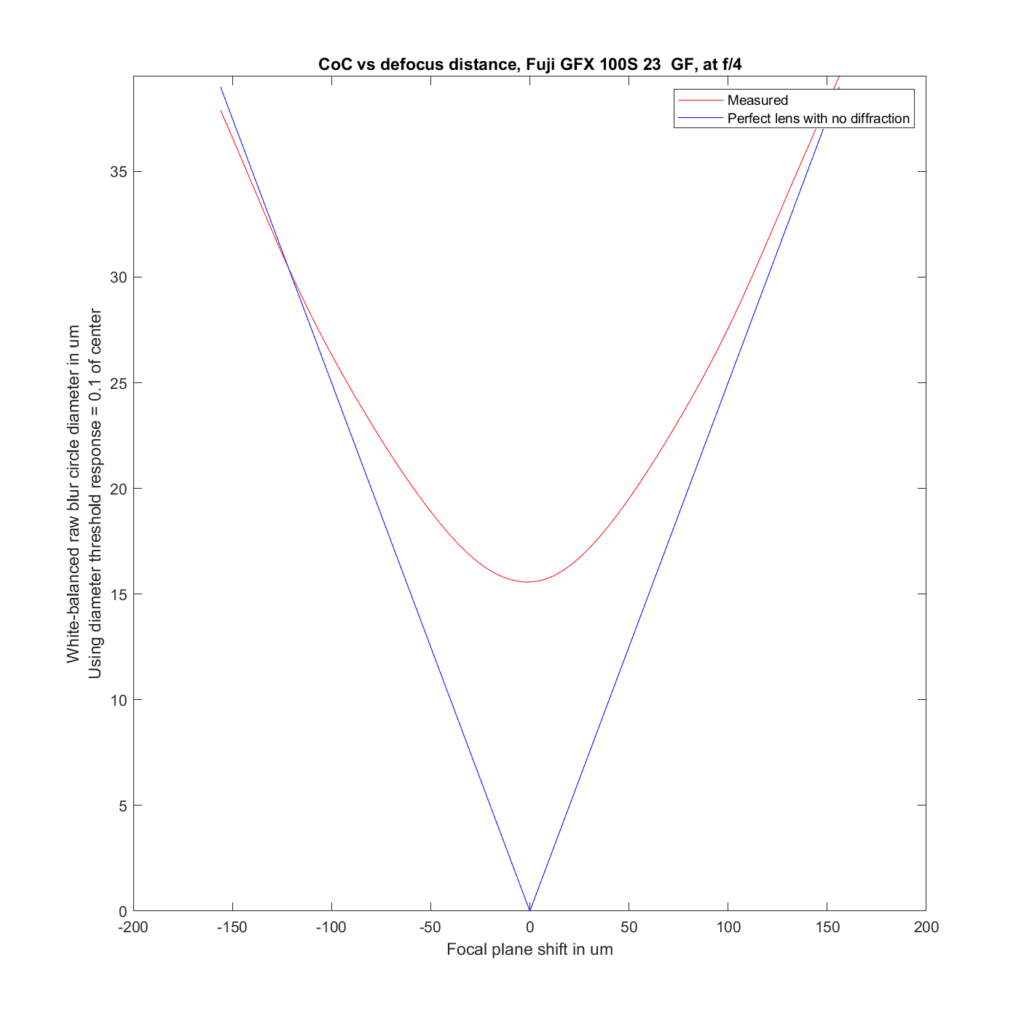
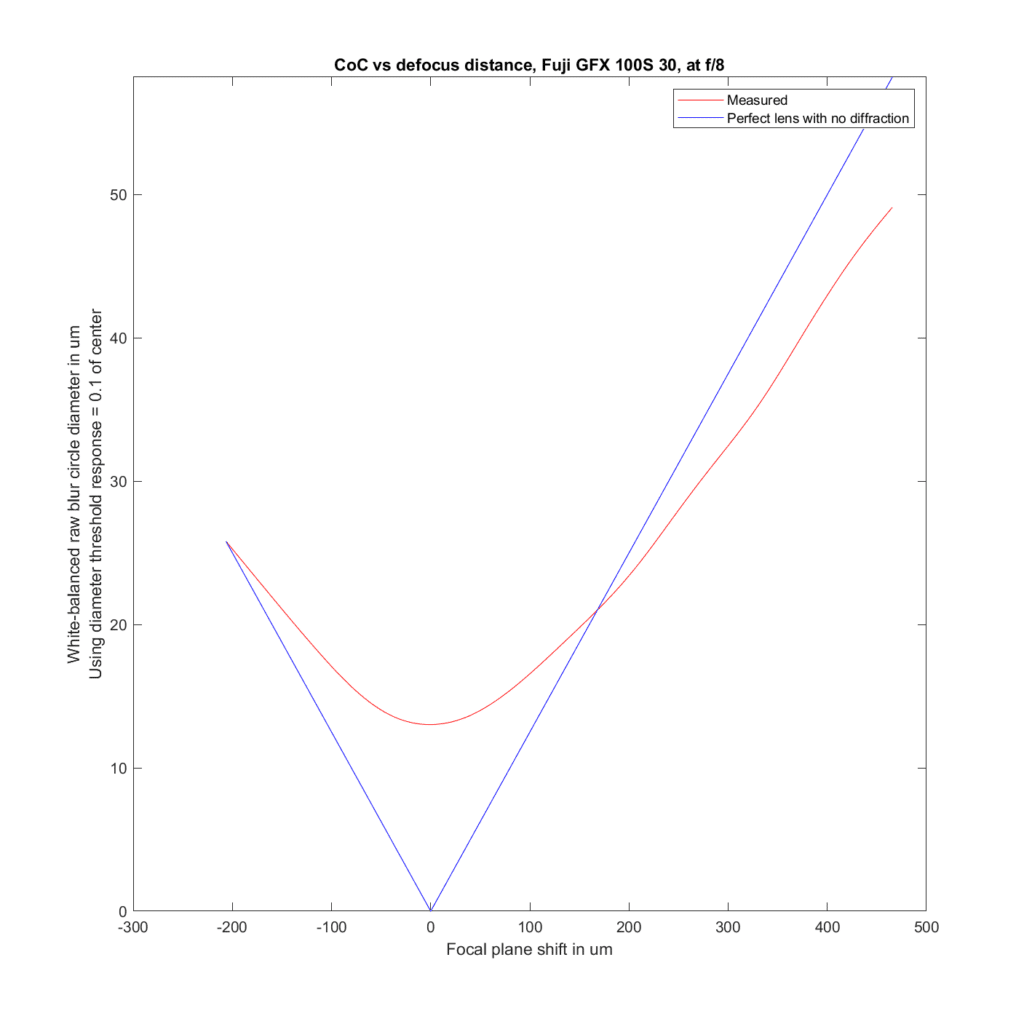
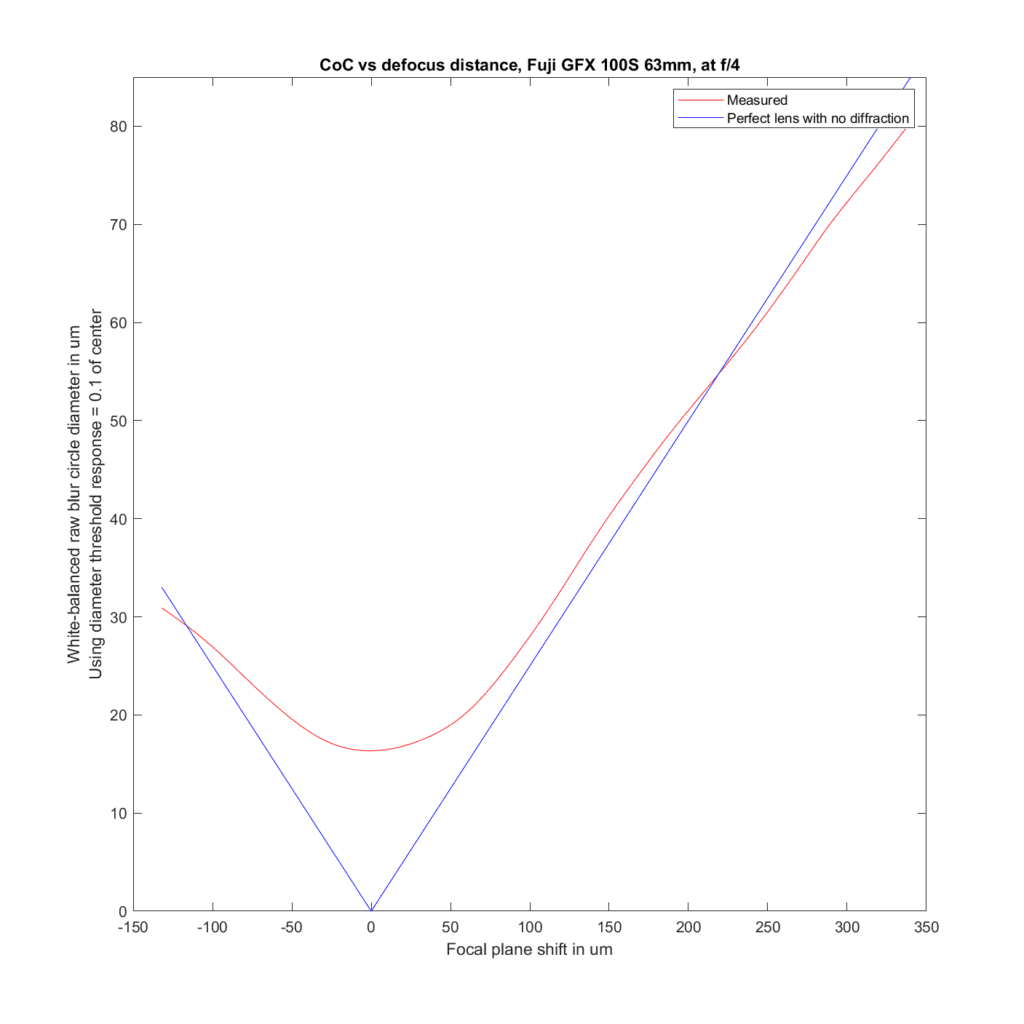
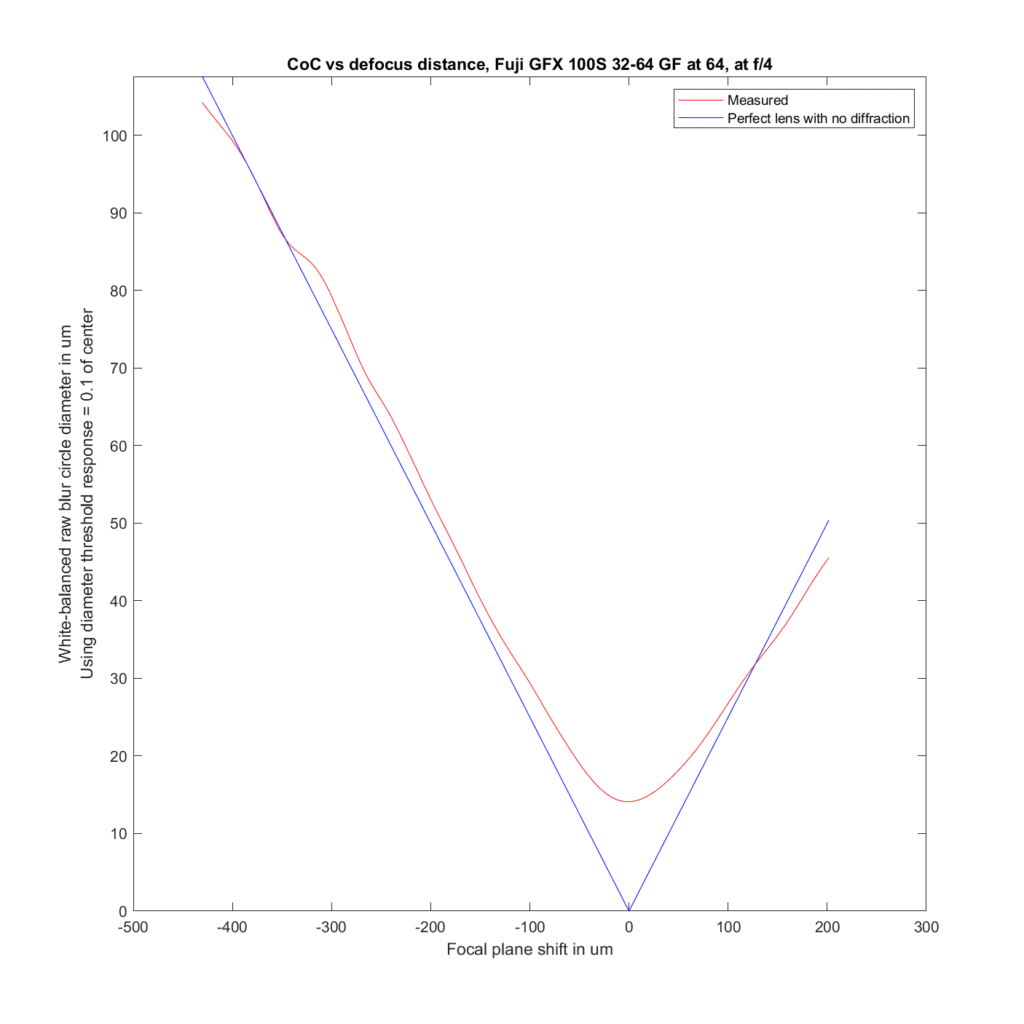
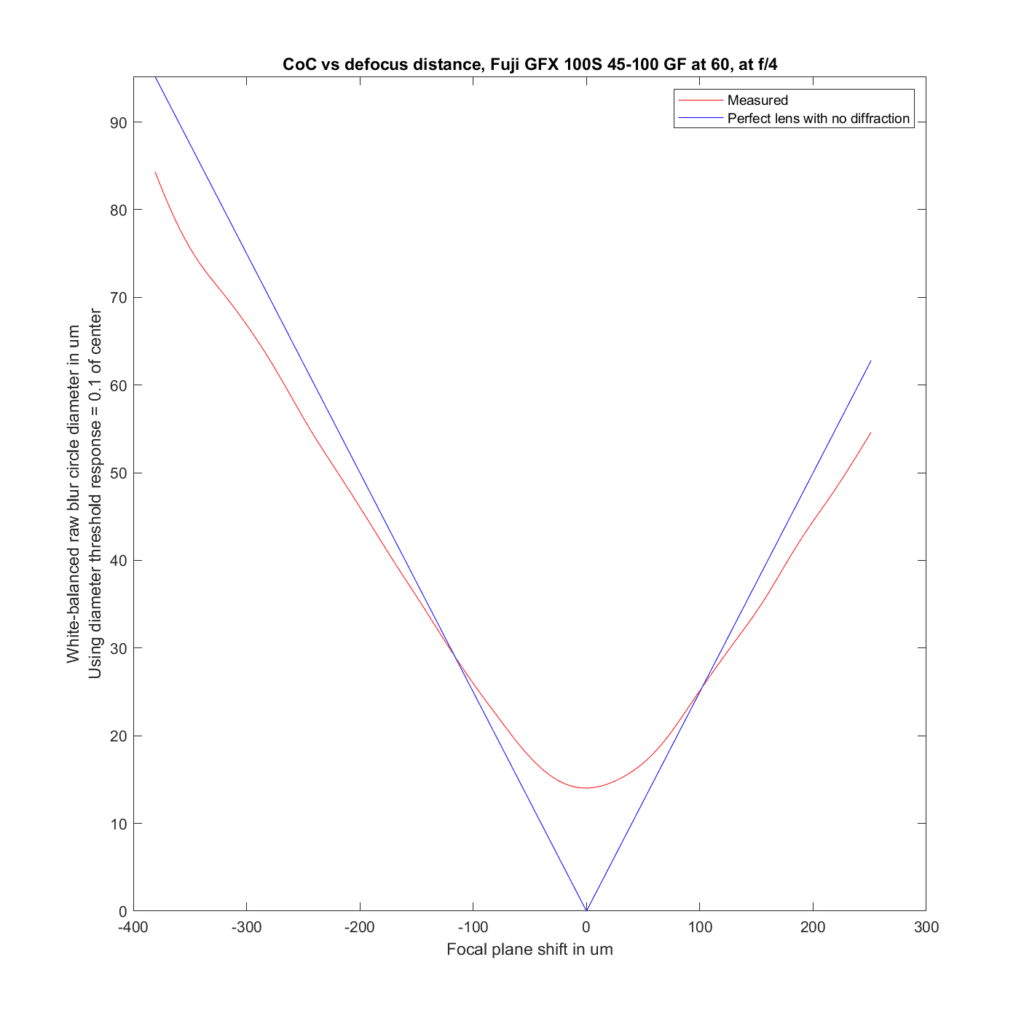
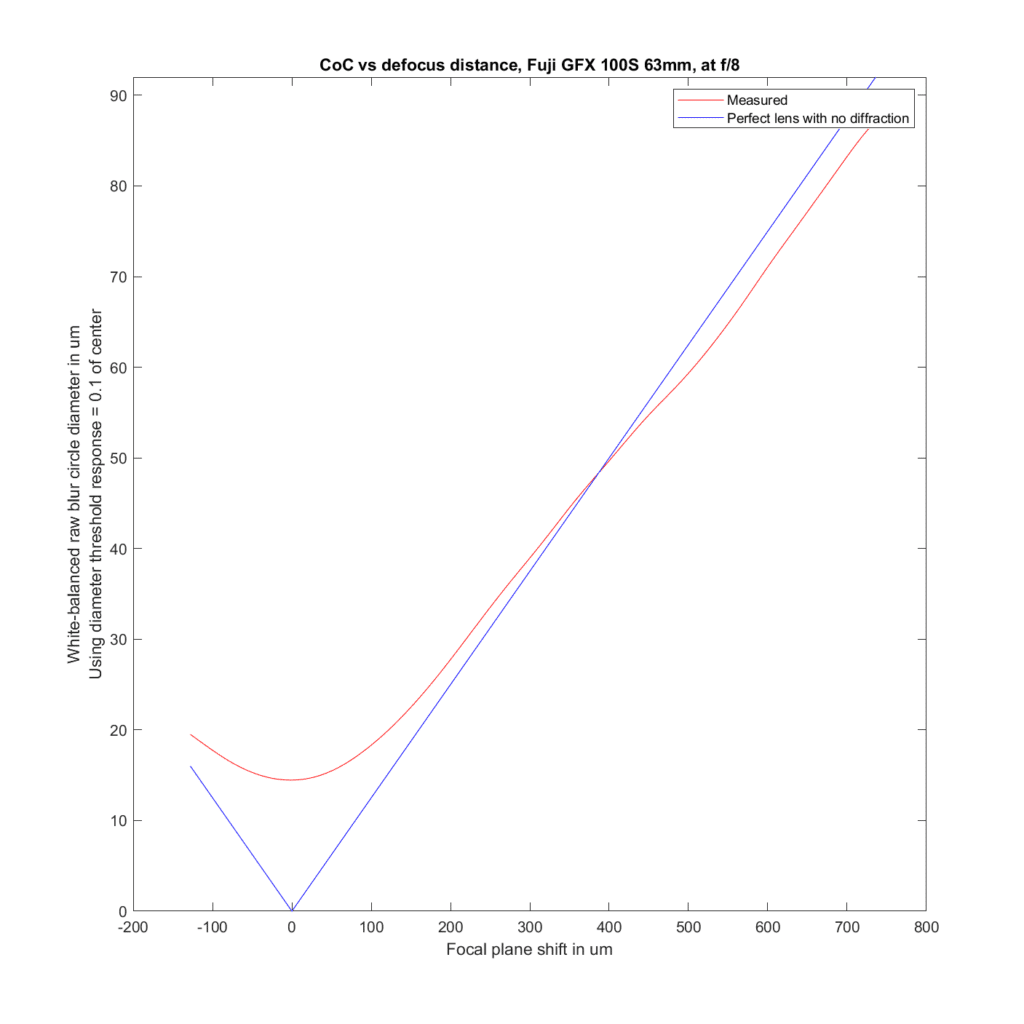
For the plots to follow, I’ve used the white-balanced raw channels as computer fodder, and used a threshold to define blur circle size that is fairly pessimistic. I take the intensity at the center of the blur circle, and define the radius of the blur circle as the distance between the center and that point where the intensity drops to one tenth of the value at the center. The blur circle data plotted above that MTF Mapper covers both sides of the line spread function or PSF, and I’m computing the radius of the blur circle both ways, averaging those two numbers, and doubling it to get the diameter of the blur circle. That gives me the red curves in the plots below. The blue curves are what geometric optics says should be the case for an ideal lens with no diffraction.
We’ll start out with the 23/4 wide open and stopped down to f/8, as you might do for landscape work.
Wide open, the 23/4 GF obeys the predictions of geometric optics quite well except for the situation where the subject is close to being in focus, at which point the images become less sharp than geometric optics predicts. This is not a surprise, since geometric optics does not consider the blurring effects of diffraction, lens aberrations, or the camera’s pixel aperture.
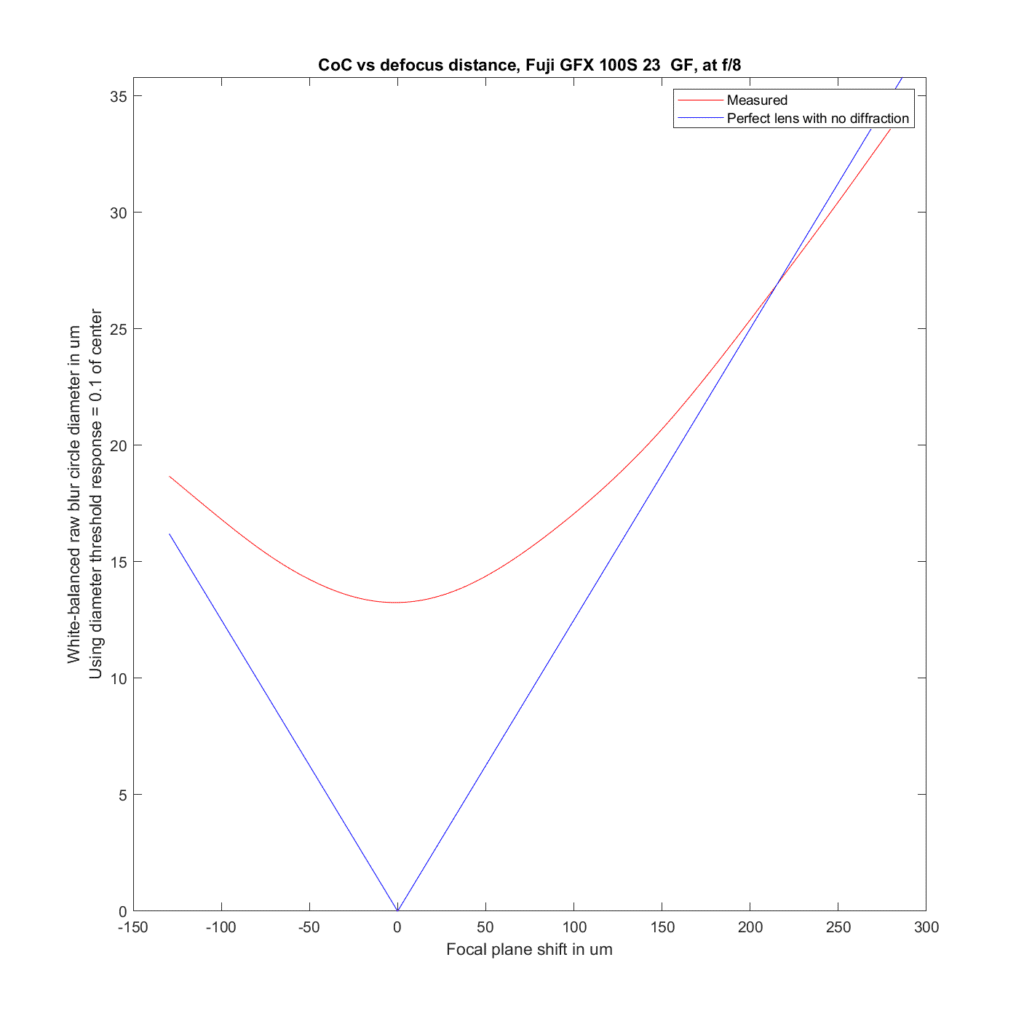
Stopping the 23/4 down to f/8:
The effect is much the same., except for the image being very slightly sharper than predicted when greatly back-focused.
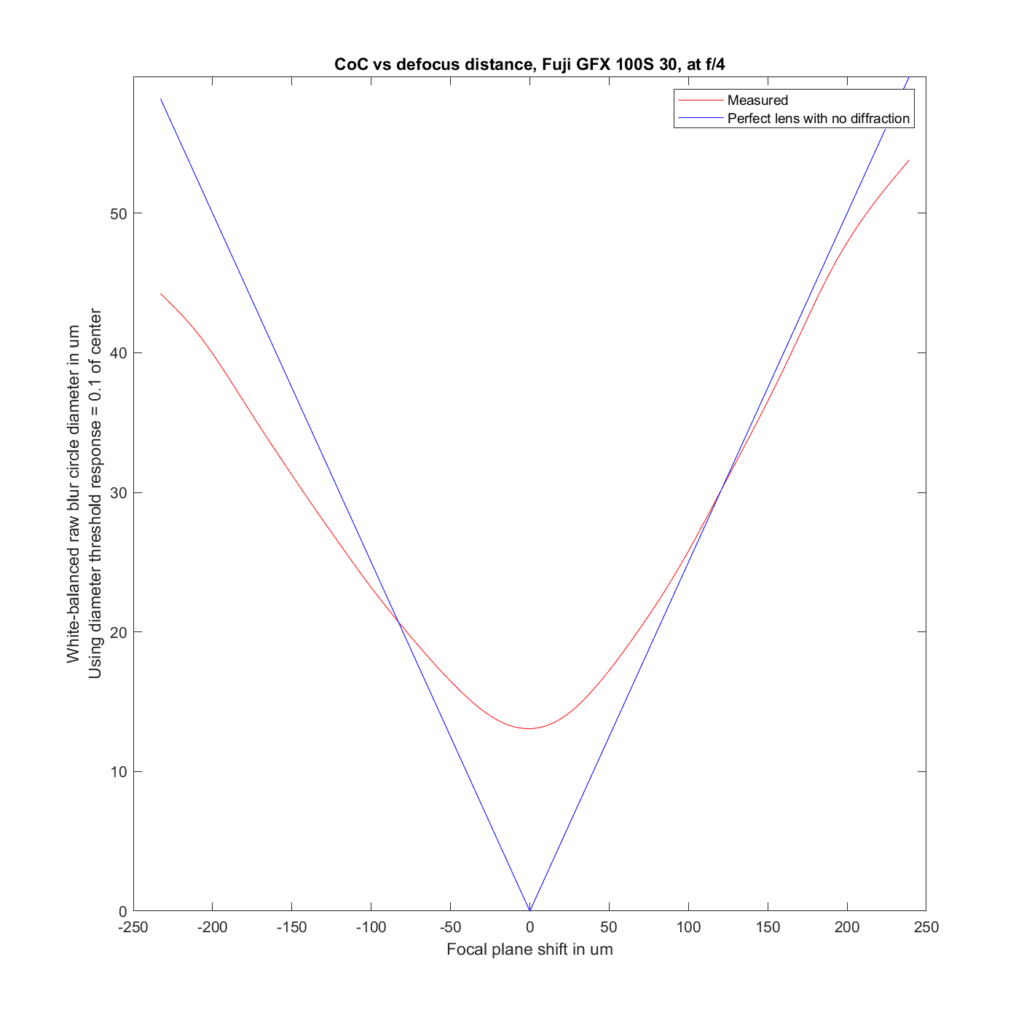
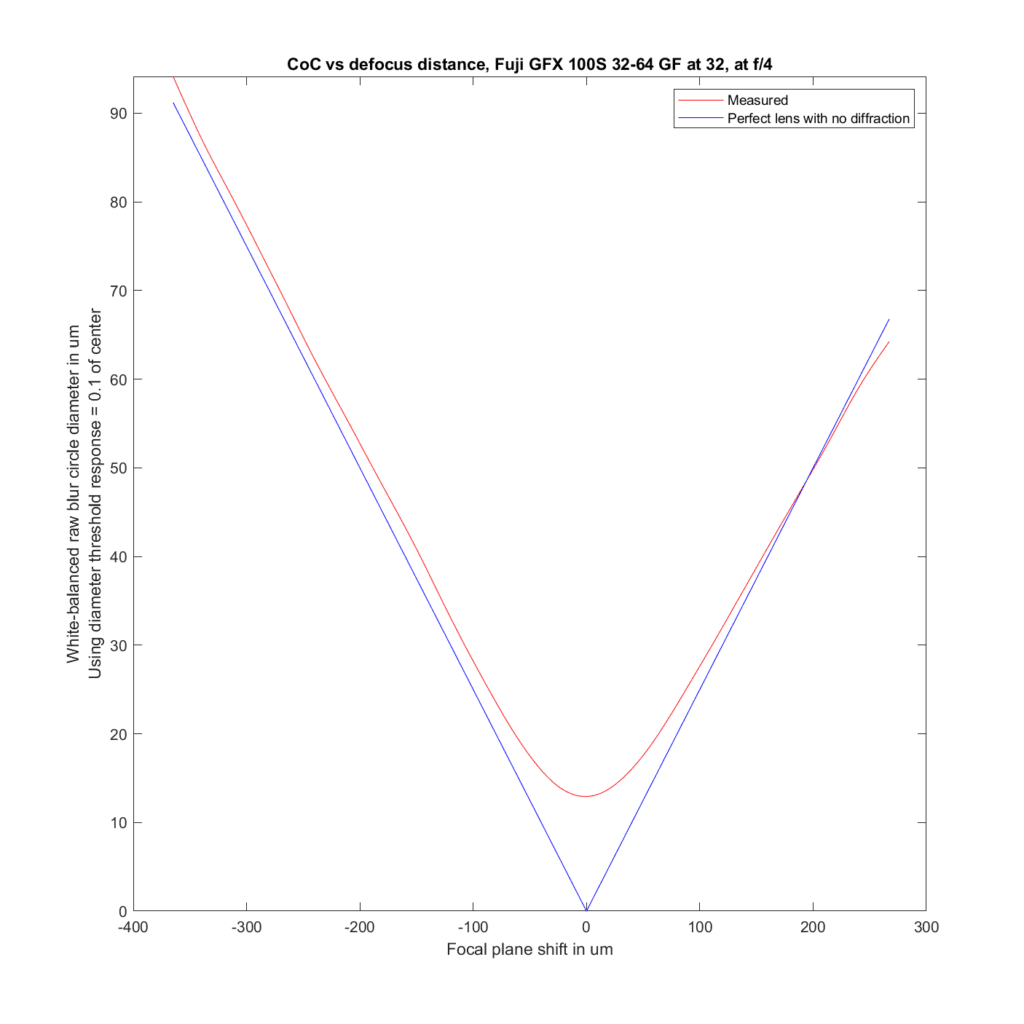
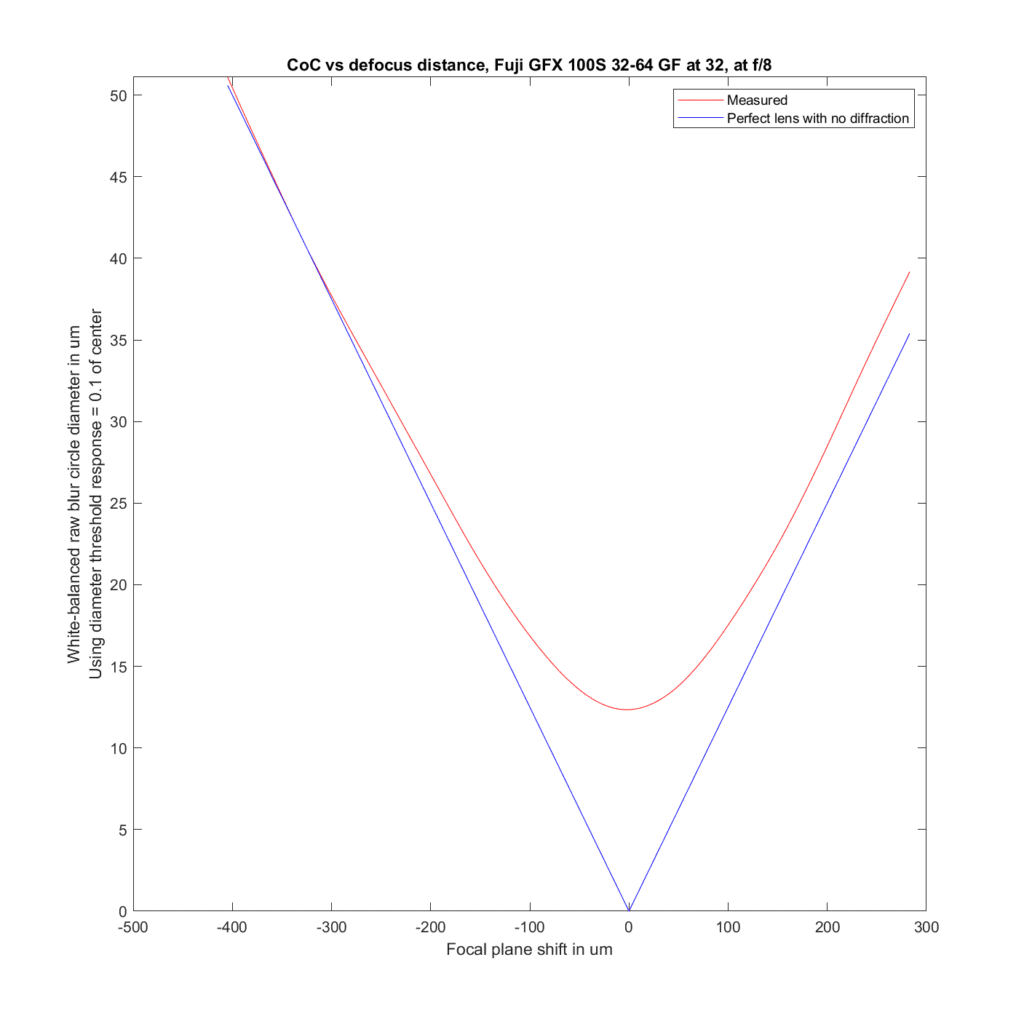
Next I’ll compare the 32-64/4 at 32 mm with the 30/3.5.
At f/4 the 30 approximately obeys theory for back-focusing, and is sharper than theory indicates for front-focusing.
The 32-64 at 32 mm and f/4 is close to what geometry predicts.
At f/8, the 30 GF produces image that are a bit sharper than geometric theory says they should be. We can’t tell what’s happening at close focusing because the series started to close to in-focus.
The 32-64 at 32 mm and f/8 is a little blurrier than a DOF calculator would say for back-focusing.
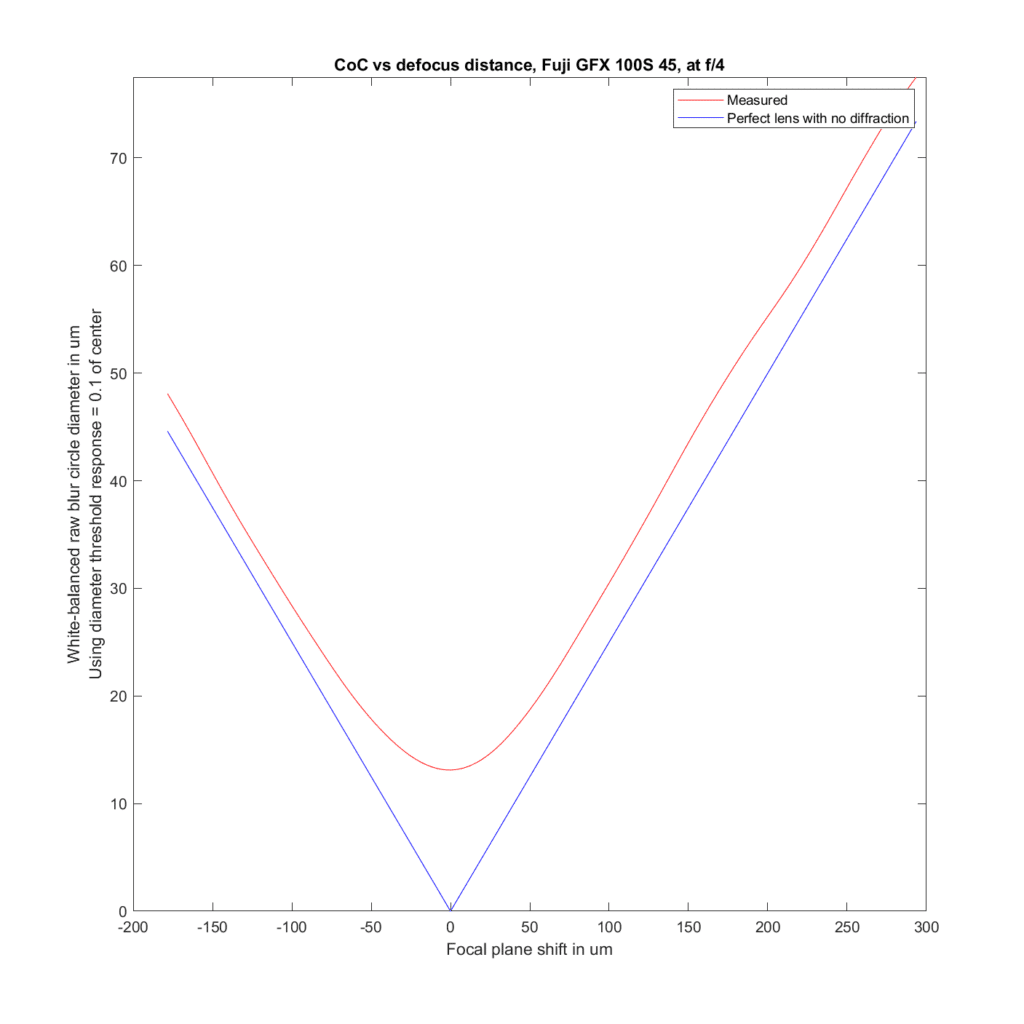
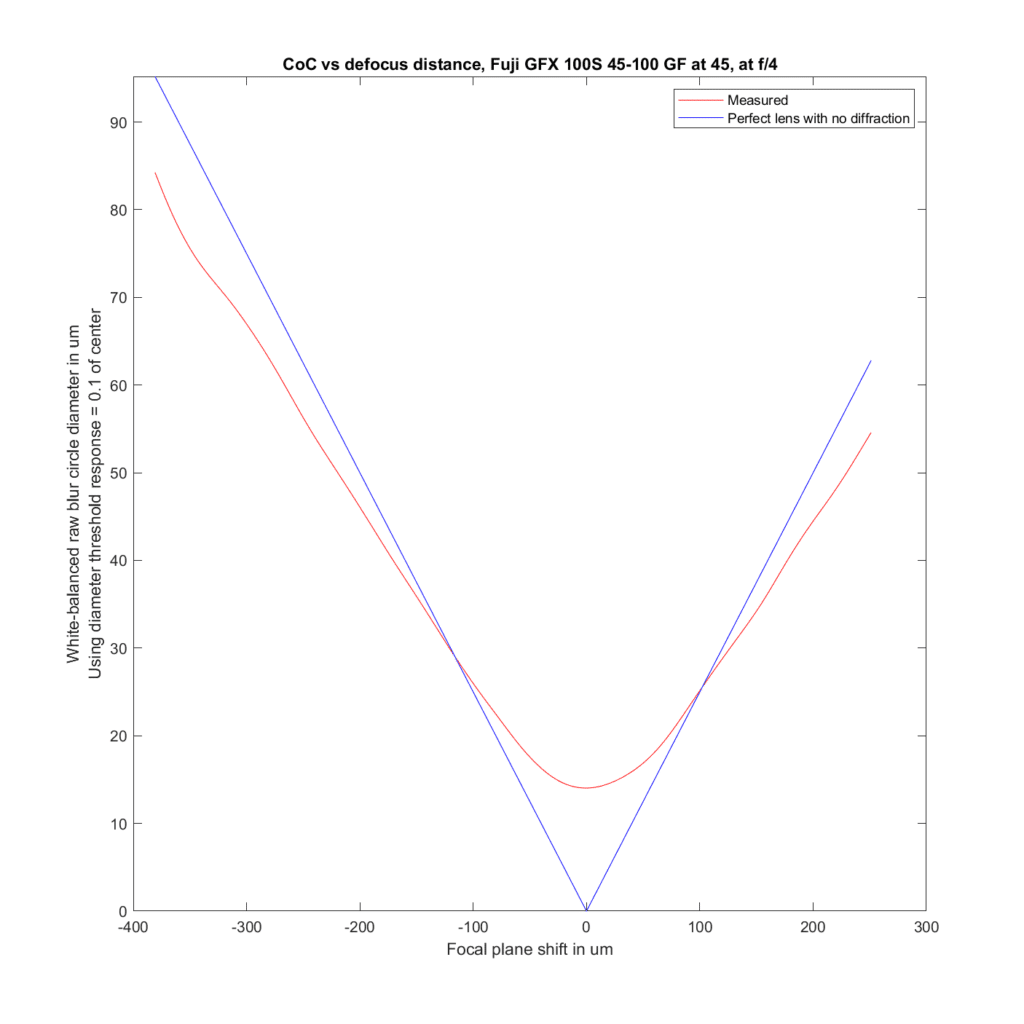
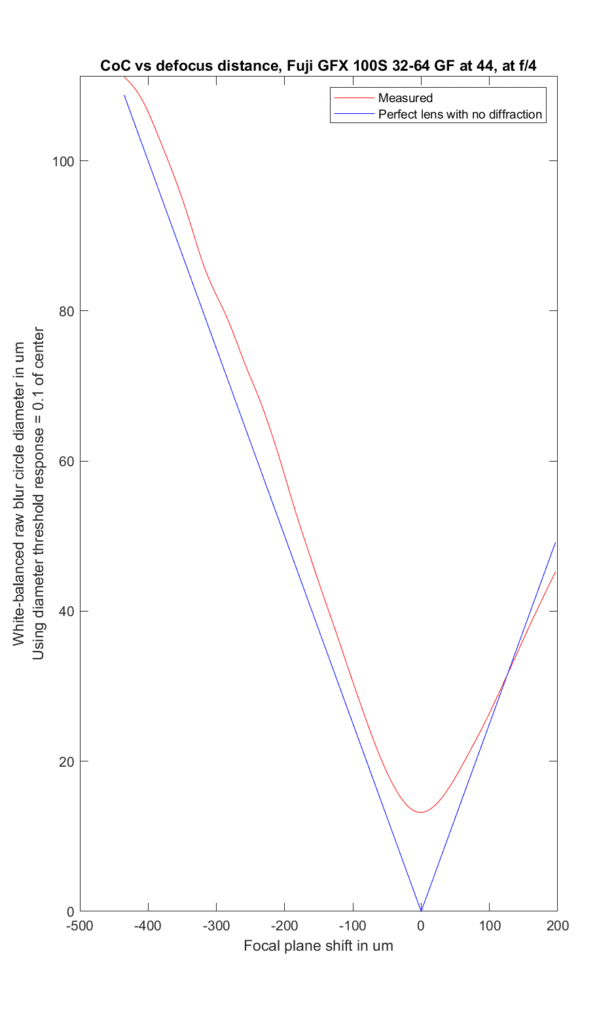
Now I’ll show you the 45/2.8 versus the 32-64/4 at 44 mm and the 45-100/4 at 45 mm
The 45 at f/4 has slightly more blur than geometric optics predicts. The 45-100 at 45 mm has less. The 32-64/4 at 44 has more for front-focusing and aboth the same for back-focusing.
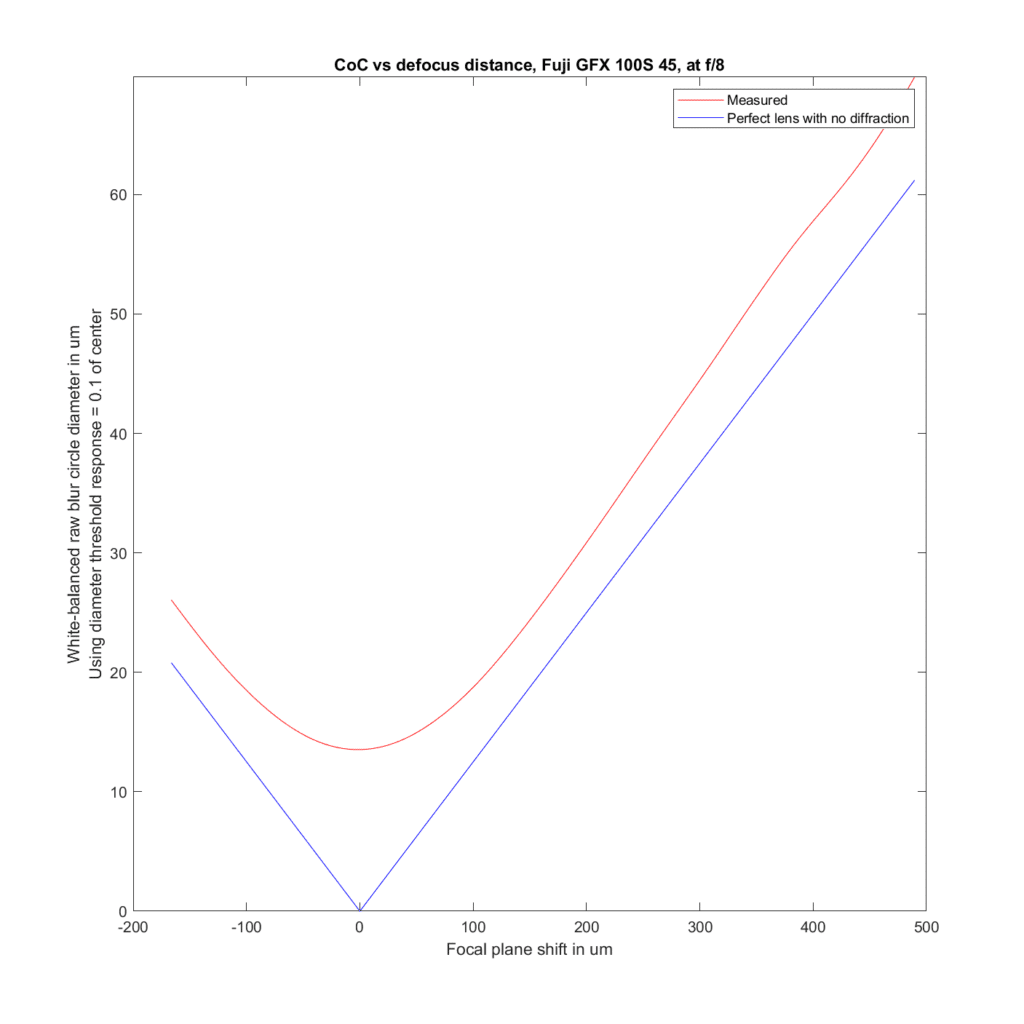
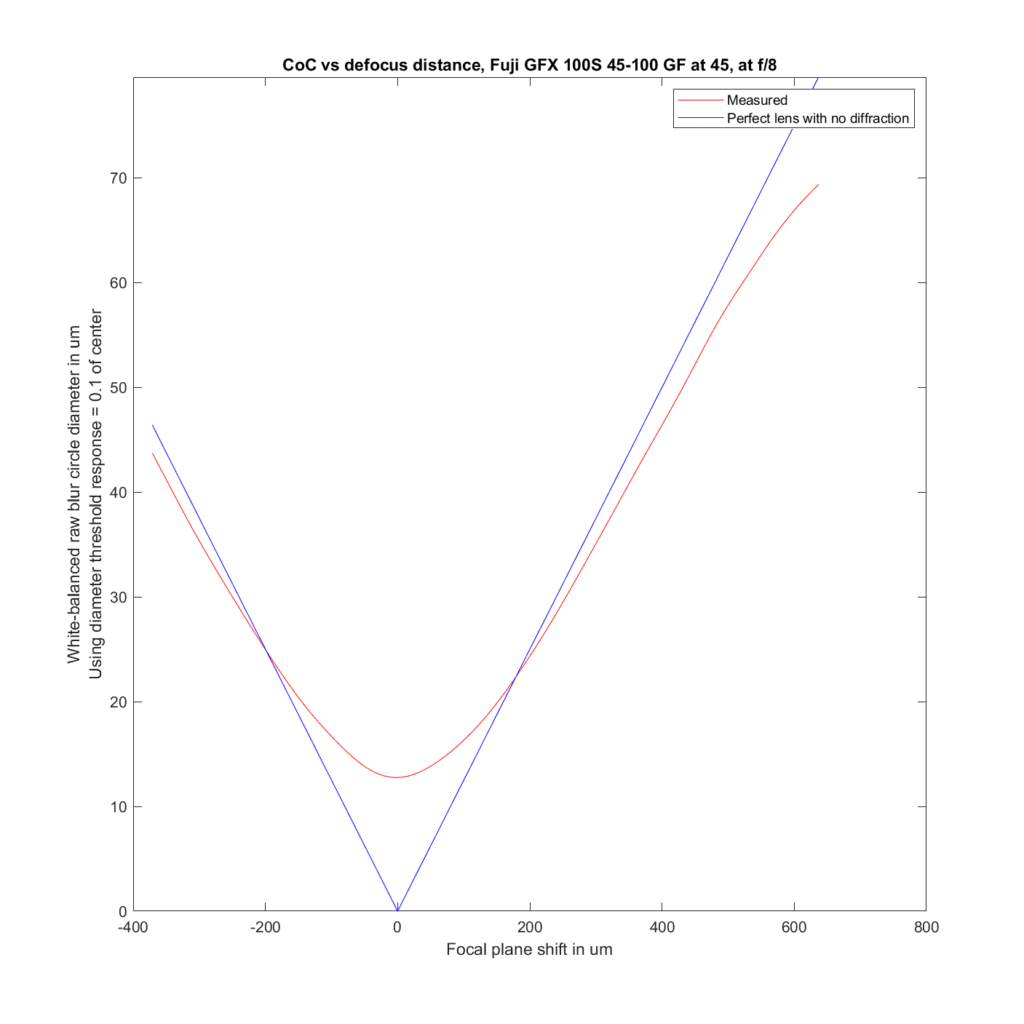
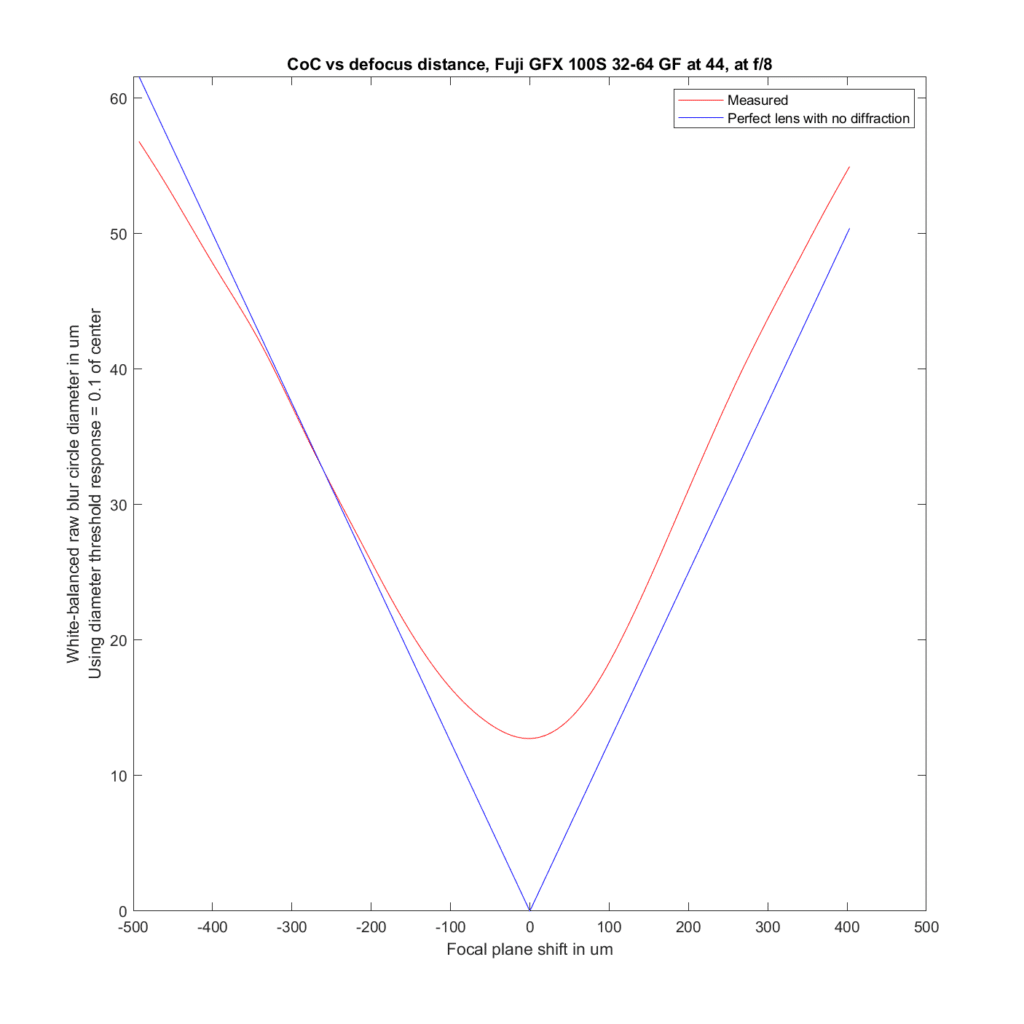
Stopped down to f/8:
the 45 and the 45-100 behave about the same, but the behavior of the 32-64 has changed.
Now let’s look at the 63, the 32-64 at 64mm, and the 45-100 at 60mm.
Good agreement in the first two, and slightly better than predicted performance with the 45-100.
Stopping down to f/8:
Outside of loss of sharpness near the focal point, even in the cases where there is the most disagreement between the actual blur circles and the predicted ones, these differences are not enough to make much difference in real world photography.
Bill Claff has made a perceptive comment:
But strictly speaking, although they correlate well, aren’t you measuring Depth of Focus?
My answer:
When I’ve tested the GFX cameras and lenses, I’ve not had access to what’s going on in the image field at all, but have figured that out from looking at captured images and paying attention to the object field. So, to the degree that I have been directly observing something, it’s been depth of field, not depth of focus.
However, in my reverse engineering of the GFX’s focus bracketing feature I have observed (ignoring and pupil magnification differences) that a step size of 1 means the camera will move the sensor 2 micrometers (um) times the f-stop in each step. THis is independent of lens focal length or focussed distance.
So the camera “thinks” in the image field. That’s one reason I’m reporting results in the image field.
The other reason is that this way I can talk about the behavior of the lenses in a manner that does not depend on a particular focused distance.
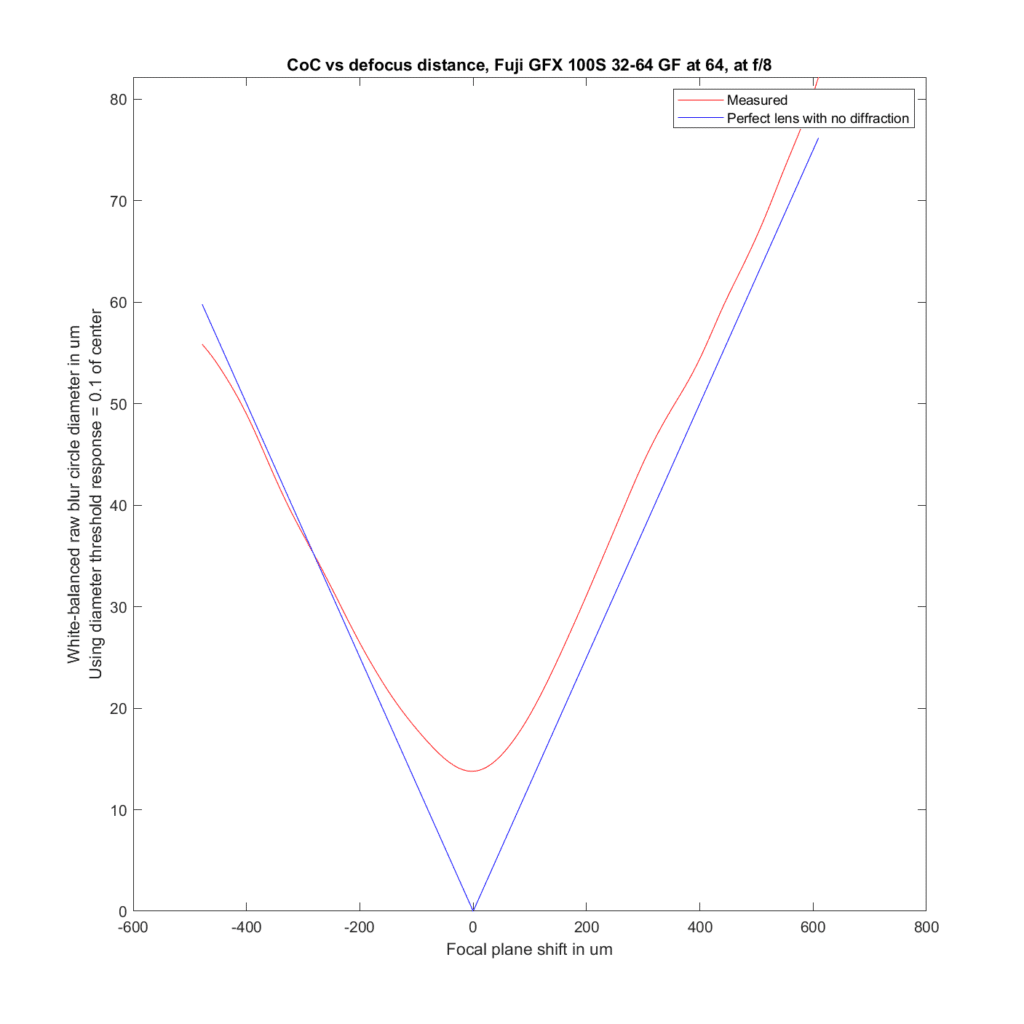
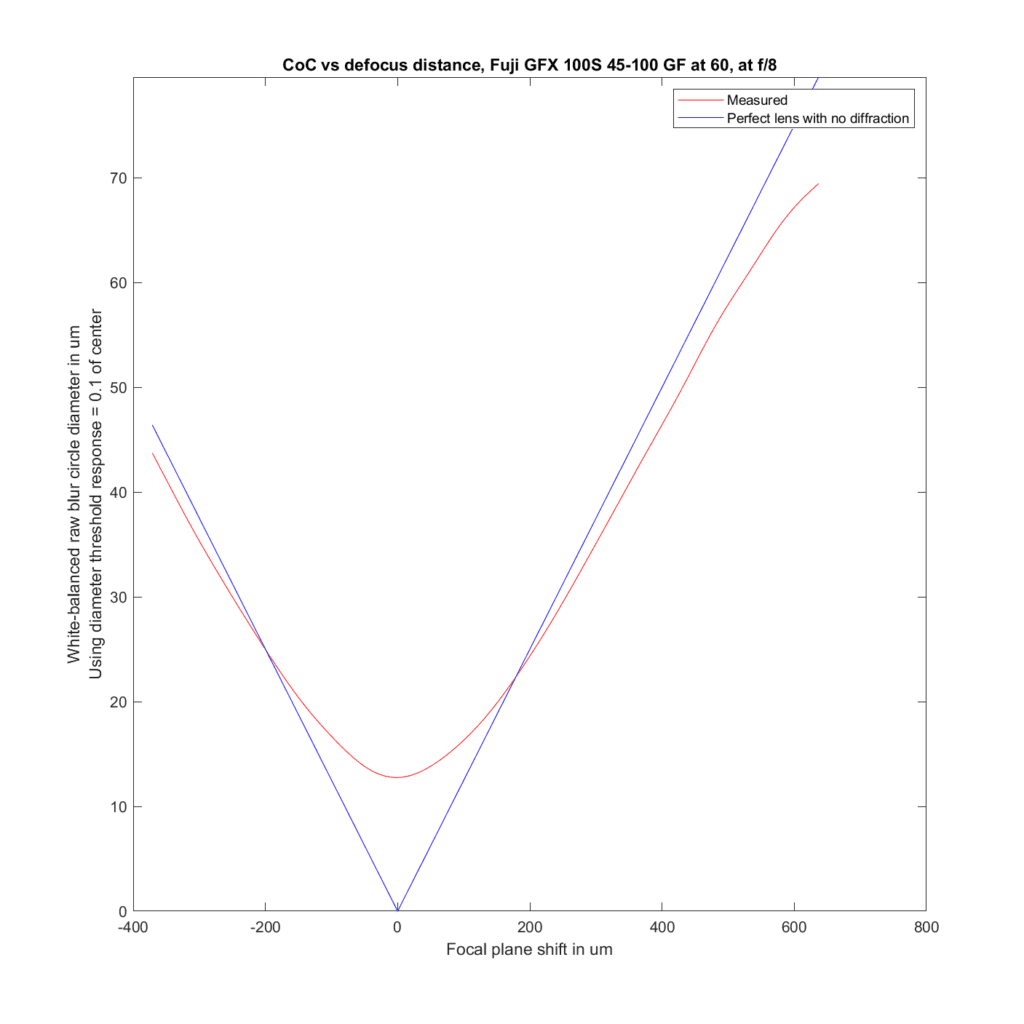
Something I note is that the blur circles seem to stay quite a bit above 10 microns, much wider than the pixel pitch.
Does that relate to using white light?
Before this series, we often often used green channel data.
Best regards
Erik
Some of that is the interaction of the LoCA with the white balancing. Some is the 10% threshold for defining the blur circle diameter.
The approximately 15um minimum blur circle average means ca. 2200 L/PH and may be considered the resolution limit of the lenses, a number amazingly similar to what we find in your MTF50 tests, except that there you used LP/PH. So, I guess you are right that the arbitrary 10% threshold is too severe. Maybe you can do a reverse engineering and calculate what threshold percentage can bring those blur circles at best focus down to ~8um, or at the precisely estimated blur size for each lens derived from the MTF50 numbers. Maybe you can set a standard for this threshold %.
I guess this would be very useful, because your graphs are very enlightening. I bet that the symmetry or differences between front and back focus are due to the lens design (symmetrical, telephoto, retro-focus…), but I would like to know if we can generalize that, so that we may expect similar behavior from lenses that were not tested this way.
And for the results that are different than prediction there is one important variable that may be acting: f-stop precision, not only for the mechanical accuracy of the diaphragm blades but also because lenses are usually labeled as lighter than they really are (a 2.8 can be in fact 2.94).