Sony 70-200/4 on an a7RII, Nikon 70-20/2.8 on a D810

Last week, I posted some images that compared the performance of the Nikon 70-200 f/2.8 GII ED to the Sony 70-200 f/4 G OSS FE when both were mounted to a Sony a7RII.

Part of the controversy related to whether eyeballing images was a useful way to compare lenses when MTF curves were available. Well, a real world image allows other things besides sharpness to be judged. Can’t argue with that, but let’s set it aside. If we’re talking sharpness, MTF, being quantitative, is better way to make most sharpness comparisons (assuming no material anisotropy, for example).

However, MTF testing is much harder to do accurately and repeatably. I’ve struggled for most of the past week. Normally, I’d take you through all the blind alleys from start to finish. However, in this case they are legion, and would serve only to confuse, so I’ll cut to the chase, post some results, then tell you how I got to them.

I tested the Nikon 70-200 f/2.8 GII ED on a Nikon D810, and the 70-200 f/4 G OSS FE on a Sony a7RII. The Sony has about 8% higher resolution, and I’m reporting the results as MTF50 in cycles/picture height, so the Sony lens/camera combination has an inherent, though difficult to quantify, advantage.

Here’s the test protocol.

• I lit an Imatest SFRPlus target with a Fotodiox 5500 degree LED flood.
• I set the lenses to 200mm focal length.
• I set the ISO to 100 on both cameras, the shutter mode to aperture, the exposure compensation to plus 1.
• I used a remote release on each camera, and invoked electronic first curtain shutter (EFCS),
• I used live view on the Nikon. The Sony always uses live view.
• I used AF-S mode, with the focus selection aimed at the Siemens star on the target. This means that the Nikon used contrast detection autofocus, and the Sony used a combination of CD and phase detection. It means that the Nikon focused at taking aperture and the Sony at some combination of apertures that is interesting and baffling to watch, and which I’ve never figured out.
• I made a series of sixteen exposures with each camera at f/16,  f/11, f/8, f/5.6, and f/4. In the case of the Nikon camera and lens, I made an additional set of exposures at f/2.8.
• I made one set of images with the target centered, and another set with the target in the corner of the frame.
• I demosaiced the images in DCRAW with these options: -v -4 -a -w -j -T -o1
• In Imatest, I measured on-axis and corner MTF50 for horizontal edges.

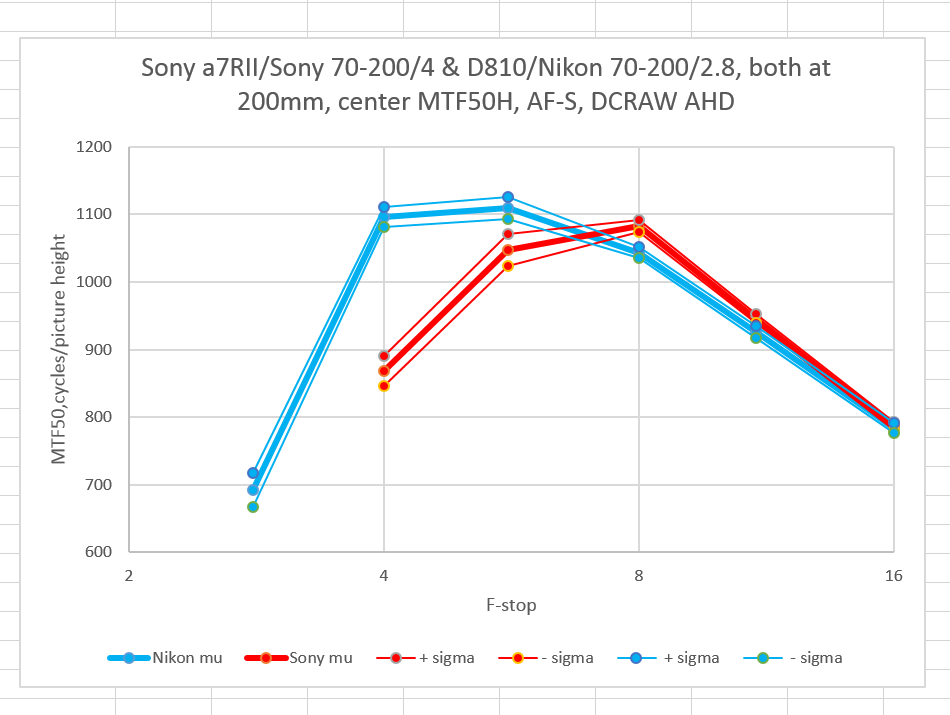
Here are the on-axis results:

The red curves are for the Sony combination, and the blue ones for the Nikon. The heavy lines are the mean results, and the lighter ones the mean plus and minus one standard deviation. The spacing is pretty tight, indicating that we can have some confidence that the autofocus systems in the two camera/lens systems are doing their job well. The Nikon system does better at f/4, and the two systems do about the same at all narrower apertures. Remember that the a7RII, being a higher res camera, has a home-field advantage here.

Also note that the absolute values for the MTF50 results are smaller than you’re probably used to seeing. That’s because I used no sharpening whatsoever in demosaicing.

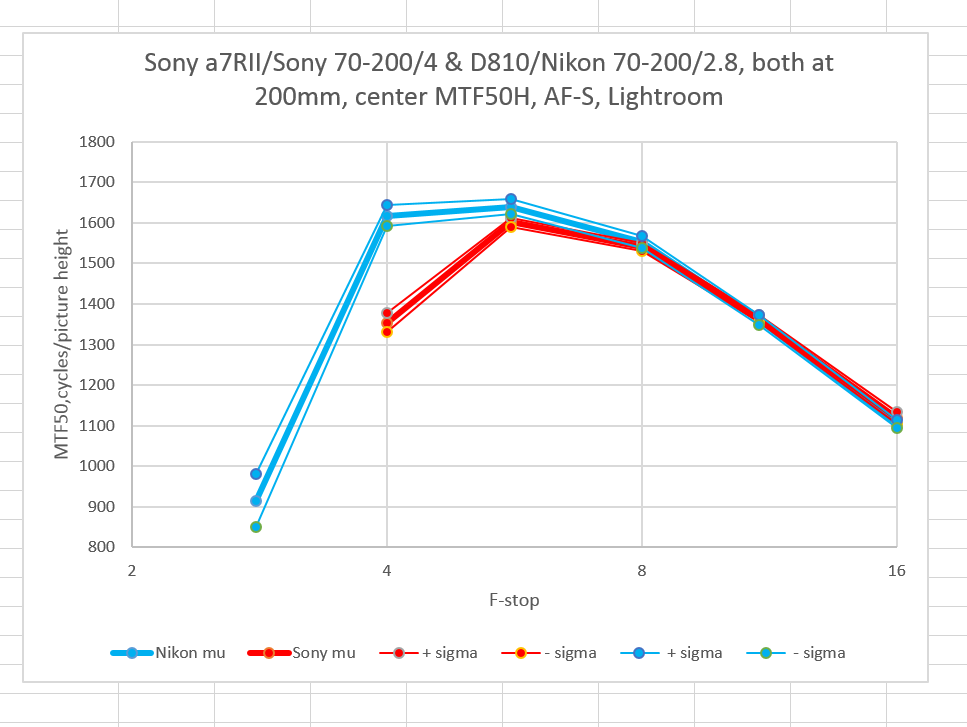
Observe the results of the above test if the images are demosaiced in Lightroom.

Center:

Note that the Sony looks slightly worse. This is not a material distinction, since Lr knows each lens. If the Nikon zoom is mounted on the Sony camera, so that Lr doesn’t know what lens it’s dealing with, it applies more sharpening than it does with the Sony zoom..

Why aren’t we looking at manually focused images? And why not images from both lenses on the a7RII? Stay tuned.