How read and quantizing noise interact

The Sony a7S has raw bit depths of 12 or 13 bits depending on the way the camera is set. It also has low read noise in many circumstances. The combination of the two conditions has lead several people to ask me if, when I think I’m measuring read noise, am I sometimes measuring just the quantizing noise of the ADC.

Good question. I built a little simulator to find out:

It models read noise as having a Gaussian distribution, and computes the sum of the read noise and the quantizing noise when the standard deviation of the read noise varies from 1/16 of the least-significant nit (LSB) of the analog-to-digital converter (ADC) to 2 LSBs. Since the quantizing noise in this case is also a function of the average (dc) level of the read noise, the little simulation models that level as varying from 0 to 1 LSB.

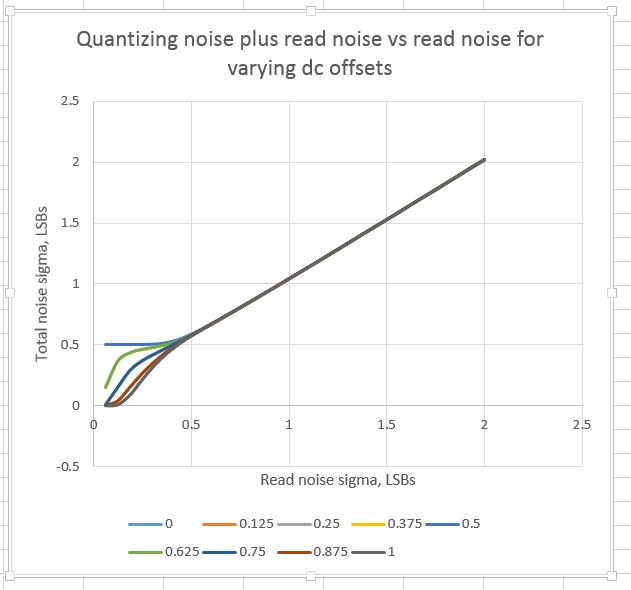
Here is the family of curves that the simulation produces:

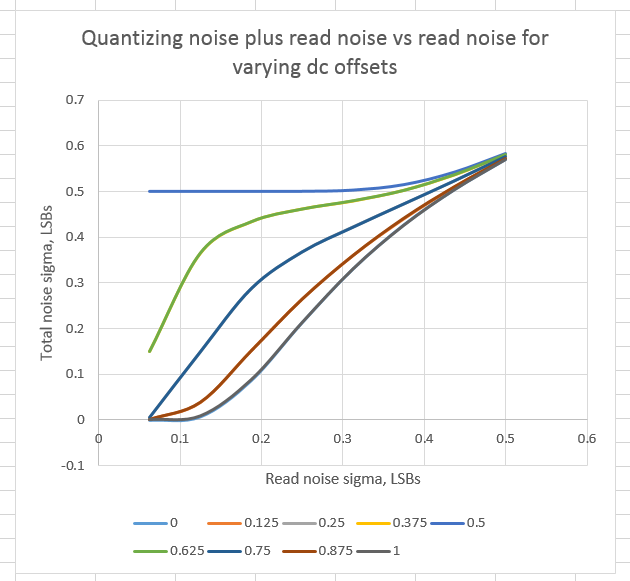
And here’s a closeup of the area around the origin:

You can see that the curves are symmetric with respect to  a dc offset of 1/2 LSB. 1/8 LSB and 7/8 LSB produce the same result, as do 1/4 LSB and 3/4 LSB. Same with 3/8 and 5/8.

You can also see that by the time the standard deviation of the read noise gets to 1/2 LSB, the dc offset doesn’t make much difference.

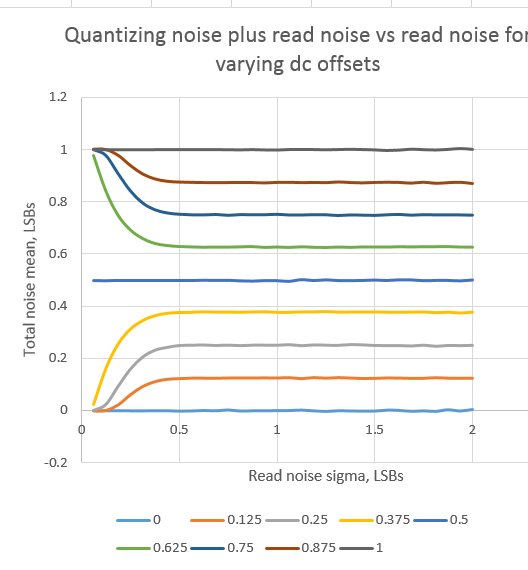
If I change the script slightly to look at the mean of the total noise instead of the standard deviation:

We get this:

This indicates that, when the read noise standard deviation is over 1/2 LSB, it supplies enough dithering to let the quantizer, on average, resolve signals that are less than one LSB.